Computer Science and Application
Vol.1 No.2(2011), Article ID:271,5 pages DOI:10.4236/csa.2011.12009
The Voronoi Diagram of Two-Dimensional Shape with Algebraic Curve Boundary
1College of Science, Zhejiang University of Technology, Hangzhou
2 College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou
3College of Business and Administration, Zhejiang University of Technology, Hangzhou
Email: shh@zjut.edu.cn
Received: Jul. 12th, 2011; revised: Jul. 25th, 2011; accepted: Aug. 9th, 2011.
ABSTRACT:
Voronoi diagram is one of the most important computational geometry concepts. It is applied widely in computer graphics, computation geometry, finite element grid partition, robot trajectory control, pattern recognition, meteorology and geology. Current 2D Voronoi diagram algorithms are constructed under the condition of point set, polygon or 2D shape with parametric curve boundary. Due to the manipulation difficulty of algebra curve, Voronoi diagram of 2D shape with algebraic curve boundary has not yet got solved. Based on interval analysis and subdivision algorithm, a new algorithm to construct the Voronoi diagram of 2D shape with algebraic curve boundary is given in this paper.
Keywords: Voronoi Diagram; Algebraic Curve; Interval Analysis; Subdivision Algorithm
以代数曲线为边界的二维形体的Voronoi图
寿华好1,袁子薇1,缪永伟2,王丽萍3
1浙江工业大学理学院,杭州
2浙江工业大学计算机科学与技术学院,杭州
3浙江工业大学经贸管理学院,杭州
Email: shh@zjut.edu.cn
摘 要:
Voronoi图是计算几何中的重要概念之一。在计算机图形学、计算几何、有限元网格划分、机器人轨迹控制、模式识别、气象学和地质学研究中得到广泛应用,现有的二维Voronoi图算法都是基于平面点集,多边形,或者以参数曲线为边界的二维形体的范围内解决的。由于代数曲线的难操作性,以代数曲线为边界的二维形体的Voronoi图算法一直未得到解决。本文在区间分析和细分算法的基础上,提出了以代数曲线为边界的二维形体的Voronoi图新算法。
收稿日期:2011年7月12日;修回日期:2011年7月25日;录用日期:2011年8月9日
关键词:Voronoi图;代数曲线;区间分析;细分算法
1. 引言
在不同的领域,Voronoi图有时也被称为Thiessen多边形、Dirichrit网格、或Wigner-Seitz域等。Voronoi图的基本定义和算法可见于许多计算几何教科书。它是关于空间邻近关系一种基础数据结构。Voronoi图有二维和三维、狭义和广义、一阶和高阶之分[1]。其中最基本、应用最广泛和研究最深入的还是二维欧氏空间平面点集Voronoi图,平面线集和面集Voronoi图可以通过平面点集Voronoi图处理近似获得[2]。平面点集Voronoi图常用构造算法主要包括矢量方法[3]和栅格方法,基于矢量的方法有增量构造算法、分治法、减量算法、平面扫描算法、间接法[1];基于栅格的方法有邻域栅格扩张法和栅格邻近归属法[4,5]。在矢量方法中,增量构造算法的时间复杂度为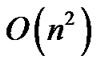 ,分治法、减量算法和平面扫描算法的时间复杂度为
,分治法、减量算法和平面扫描算法的时间复杂度为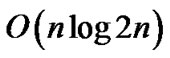 ,间接法的时间复杂度取决于其对偶Delaunay三角网获取的时间复杂度。现有矢量构造算法存在计算繁琐、数据结构复杂、存在累计误差、存储空间开销大等不足,而简单的栅格构造算法在精度与空间复杂度以及时间复杂度之间存在严重矛盾,一般只适用于精度和效率要求较低、小规模数据场合,而且获得的只是近似的Voronoi图,所以应用范围受到限制[5]。
,间接法的时间复杂度取决于其对偶Delaunay三角网获取的时间复杂度。现有矢量构造算法存在计算繁琐、数据结构复杂、存在累计误差、存储空间开销大等不足,而简单的栅格构造算法在精度与空间复杂度以及时间复杂度之间存在严重矛盾,一般只适用于精度和效率要求较低、小规模数据场合,而且获得的只是近似的Voronoi图,所以应用范围受到限制[5]。
在Voronoi图中,被用来划分空间的各个基本图形元素一般被称为站点。最基本的Voronoi图是以平面点为站点的平面点集P的Voronoi图,它将平面划分成凸多边形形状的Voronoi区域,P中的每个站点![]() ,对应一个这样区域
,对应一个这样区域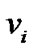 ,使得
,使得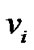 内的任何点距离
内的任何点距离![]() ,比距离其它站点近。Voronoi图的定义可以推广到三维或高维,也可以推广到二阶或高阶(以两个站点或多个站点为一组划分邻近区域),也可以推广到
,比距离其它站点近。Voronoi图的定义可以推广到三维或高维,也可以推广到二阶或高阶(以两个站点或多个站点为一组划分邻近区域),也可以推广到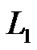 或
或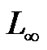 等其他度量,也可以进一步推广到站点包括线段或多边形的广义Voronoi图[1,2],也可以有距离的推广、生长元的推广等[6]。著名的应用包括机器人运动规划、形状表示、转换和网格生成[2]。
等其他度量,也可以进一步推广到站点包括线段或多边形的广义Voronoi图[1,2],也可以有距离的推广、生长元的推广等[6]。著名的应用包括机器人运动规划、形状表示、转换和网格生成[2]。
前面提到的Voronoi图主要针对的是点集模型、多边形模型和参数曲线曲面模型[7],而计算机辅助几何设计中曲线的表示有参数形式和代数形式,曲线的参数和代数表示在几何造型中各有优缺点,CAGD中同时采用曲线的两种表示法,两种形式间的转换成为必须解决的课题。参数曲线的代数化总是可以实现的,但大部分代数曲线都不能精确参数化。近年来随着计算机计算能力的大幅提升,代数曲线曲面在几何造型和图形学中的应用越来越多[8],在对用代数曲线曲面造型的几何体进行后续操作(比如中轴提取,形状匹配,有限元网格划分)的时候经常需要先知道该几何体的Voronoi图,从而用代数曲线曲面构造的二维或者三维形体的Voronoi图计算也就显得十分必要。然而到目前为止对于代数曲线曲面的Voronoi图计算还未有人涉及。本文在区间分析[9]和细分算法的基础上提出了一种以代数曲线为边界的二维形体的Voronoi图新算法。基本思想是通过对代数曲线段进行采样得到几组像素点集合,从而以代数曲线为边界的二维形体的Voronoi图计算转换为求解最短距离至少在两组以上像素点集合处达到的像素全体,在求解过程中借助于四叉树和区间算术进行加速。
2. 算法
假设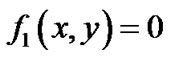 ,
, 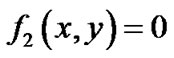 ,
, 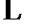 ,
,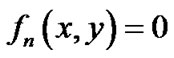 是给定的n条平面代数曲线,其中
是给定的n条平面代数曲线,其中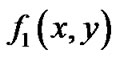 ,
, 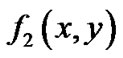 ,
, 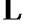 ,
,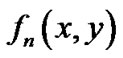 是二元多项式,这n条平面代数曲线构成了一个二维形体,所考虑的平面矩形区域是
是二元多项式,这n条平面代数曲线构成了一个二维形体,所考虑的平面矩形区域是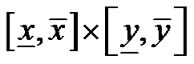 ,像素点大小(即像素点的长度或宽度)为
,像素点大小(即像素点的长度或宽度)为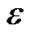 。计算该平面矩形区域内这n条代数曲线所围成的二维形体的Voronoi图,相当于计算该平面矩形区域内到这些代数曲线的最短距离至少有两处达到的像素点全体。
。计算该平面矩形区域内这n条代数曲线所围成的二维形体的Voronoi图,相当于计算该平面矩形区域内到这些代数曲线的最短距离至少有两处达到的像素点全体。
算法的第一个关键步骤是首先利用四叉树和区间算术将这n条代数曲线离散化。即分别找出包含这n条代数曲线的像素点的n个集合
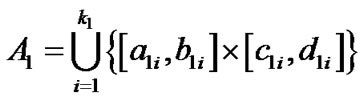 ,
,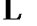 ,
,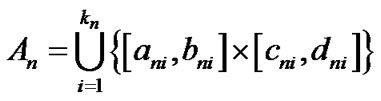 。先通过修正仿射算术[10]计算
。先通过修正仿射算术[10]计算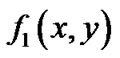 在
在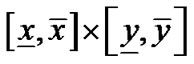 上的取值范围
上的取值范围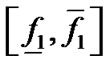 ,然后判断
,然后判断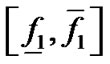 是否包含0,如果
是否包含0,如果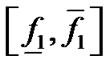 不包含0,说明
不包含0,说明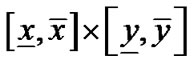 内不包含代数曲线
内不包含代数曲线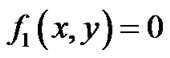 ,则抛弃该区域,否则如果
,则抛弃该区域,否则如果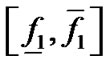 包含0,说明
包含0,说明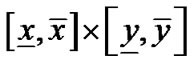 有可能包含代数曲线
有可能包含代数曲线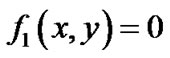 ,则将该平面矩形区域在中点处一分为四,通过四叉树算法的递归过程使得细分后的区域逐渐减小,一直细分到区域的大小即区域的长和宽都小于等于一个像素的大小
,则将该平面矩形区域在中点处一分为四,通过四叉树算法的递归过程使得细分后的区域逐渐减小,一直细分到区域的大小即区域的长和宽都小于等于一个像素的大小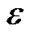 为止,如果还是排除不掉,则将该区域存入
为止,如果还是排除不掉,则将该区域存入![]() ,同理可得
,同理可得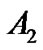 ,
,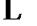 ,
,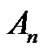 。这里特别值得一提的是:如果不用四叉树,那么需要对每个像素进行判断,比较费时间。而使用四叉树,那么当
。这里特别值得一提的是:如果不用四叉树,那么需要对每个像素进行判断,比较费时间。而使用四叉树,那么当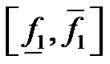 不包含0时,整个区域
不包含0时,整个区域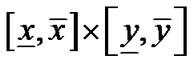 可以抛掉,不需要对这个区域内的像素作进一步的判断,而能不能把一个不包含代数曲线的区域成功地抛掉又取决于所使用的区间算术的精确度,这也是为什么我们选用相对比较精确的修正仿射算术的原因。总之四叉树数据结构和相对比较精确的区间算术可以起到计算加速的作用。
可以抛掉,不需要对这个区域内的像素作进一步的判断,而能不能把一个不包含代数曲线的区域成功地抛掉又取决于所使用的区间算术的精确度,这也是为什么我们选用相对比较精确的修正仿射算术的原因。总之四叉树数据结构和相对比较精确的区间算术可以起到计算加速的作用。
算法的第二个关键步骤是计算出平面矩形区域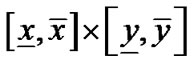 内到这n组像素集合
内到这n组像素集合![]() ,
,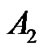 ,
,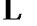 ,
,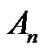 最短距离至少在两处达到的像素点集合M。这个问题仍然是通过区间算术和四叉树解决的,先用普通区间算术逐个计算平面矩形区域
最短距离至少在两处达到的像素点集合M。这个问题仍然是通过区间算术和四叉树解决的,先用普通区间算术逐个计算平面矩形区域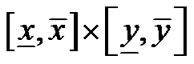 和像素
和像素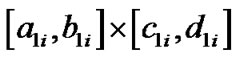 之间的区间距离
之间的区间距离
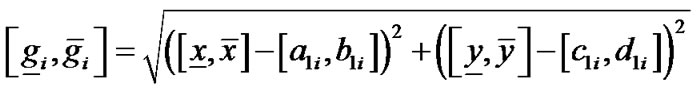 ,
,
再令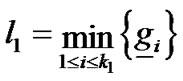 ,
,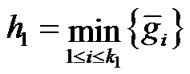 ,那么区间
,那么区间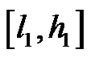 就是平面矩形区域
就是平面矩形区域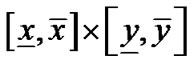 到代数曲线
到代数曲线![]() 的最短距离区间,同理可得平面矩形区域
的最短距离区间,同理可得平面矩形区域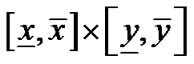 到代数曲线
到代数曲线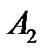 的最短距离区间
的最短距离区间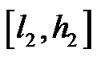 ,
,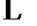 ,平面矩形区域
,平面矩形区域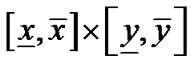 到代数曲线
到代数曲线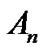 的最短距离区间
的最短距离区间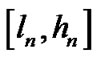 。
。
再令 ,
,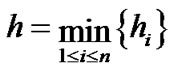 ,则
,则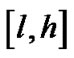 是平面矩形区域
是平面矩形区域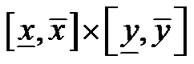 到n条代数曲线的最短距离区间。如果
到n条代数曲线的最短距离区间。如果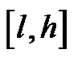 与
与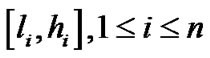 中只有一个区间相交,那么
中只有一个区间相交,那么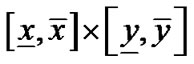 不可能包含Voronoi图的点,从而可以抛弃
不可能包含Voronoi图的点,从而可以抛弃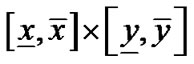 ,但是如果
,但是如果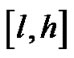 与
与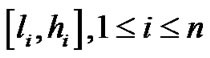 中至少两个区间相交,则此时
中至少两个区间相交,则此时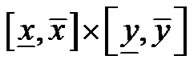 可能包含Voronoi图的点,此时将
可能包含Voronoi图的点,此时将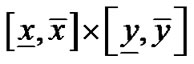 在中点处一分为四,仍然是通过四叉树递归过程使得细分后的区域逐渐减小,一直细分到区域的大小即区域的长和宽都小于等于一个像素的大小
在中点处一分为四,仍然是通过四叉树递归过程使得细分后的区域逐渐减小,一直细分到区域的大小即区域的长和宽都小于等于一个像素的大小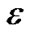 为止,如果还是排除不掉,则将该区域存入M。那么M就是我们所要计算的以代数曲线为边界的二维形体的Voronoi图。具体算法如下:
为止,如果还是排除不掉,则将该区域存入M。那么M就是我们所要计算的以代数曲线为边界的二维形体的Voronoi图。具体算法如下:
(1) 输入代数曲线段的多项式函数表达式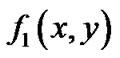 ,
,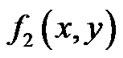 ,
,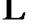 ,
,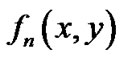 ,以及所在的平面矩形区域
,以及所在的平面矩形区域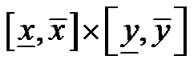 和像素的大小
和像素的大小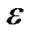 。
。
(2) 利用修正仿射算术计算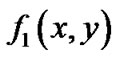 在区域
在区域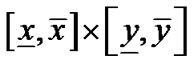 上的取值范围
上的取值范围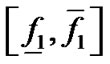 ,如果
,如果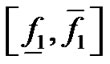 不包含0,则将该区域剔除,否则将该区域在其中点处一分为四个小区域,对每个小区域重复步骤(2),一直细分到区域的大小为小于等于一个像素的大小
不包含0,则将该区域剔除,否则将该区域在其中点处一分为四个小区域,对每个小区域重复步骤(2),一直细分到区域的大小为小于等于一个像素的大小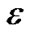 为止,如果还是排除不掉,则将其存入
为止,如果还是排除不掉,则将其存入![]() ,最后得
,最后得
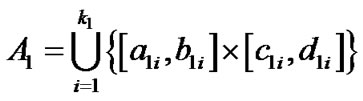 。
。
(3) 同理可得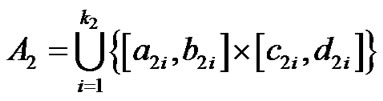 ,
,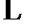 ,
,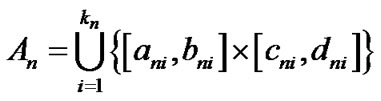 。
。
(4) 利用普通区间算术计算
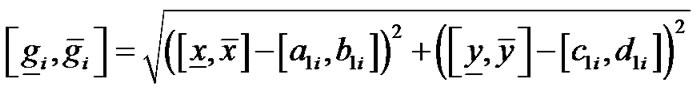 ,
,
然后令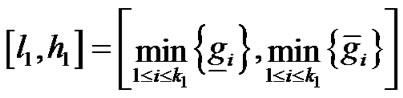 ,同理可得
,同理可得
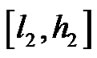 ,
,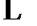 ,
,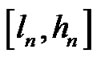 ,再令
,再令 ,
,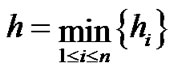 ,
,
如果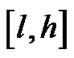 与
与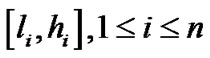 中只有一个区间相交,那么抛弃
中只有一个区间相交,那么抛弃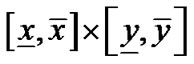 ,如果
,如果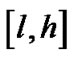 与
与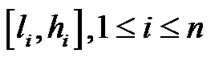 中至少两个区间相交,则将区域
中至少两个区间相交,则将区域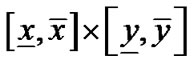 在其中点处一分为四个小区域,对每个小区域重复步骤(4),一直细分到区域的大小为小于等于一个像素的大小
在其中点处一分为四个小区域,对每个小区域重复步骤(4),一直细分到区域的大小为小于等于一个像素的大小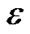 为止,如果还是排除不掉,则将其存入M。
为止,如果还是排除不掉,则将其存入M。
(5) 作出代数曲线![]() ,
,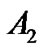 ,
, 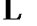 ,
,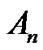 以及Voronoi图M,算法结束。
以及Voronoi图M,算法结束。
3. 实例
我们用Mathematica5.0编程实现上面的算法,并在中央处理器为Intel® Pentium® CPU T2330 @ 1.60 GHz的微机系统里运行该程序进行了一些实例的计算,下面给出四个例子。
例1:两条代数曲线分别取为直线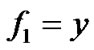 和抛物线
和抛物线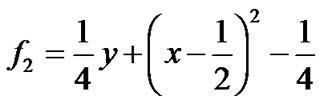 在平面区域
在平面区域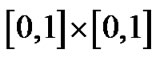 内的部分。这两条代数曲线的方程相对来说比较简单。图1是计算结果:总的CPU运行时间是2044.63秒,总的细分次数是3301次,包括两条代数曲线构成的2维形体和它们的Voronoi图在内的总的像素是3884个。从图1可以看出,Voronoi图与中轴(medial axis)的不同之处。
内的部分。这两条代数曲线的方程相对来说比较简单。图1是计算结果:总的CPU运行时间是2044.63秒,总的细分次数是3301次,包括两条代数曲线构成的2维形体和它们的Voronoi图在内的总的像素是3884个。从图1可以看出,Voronoi图与中轴(medial axis)的不同之处。
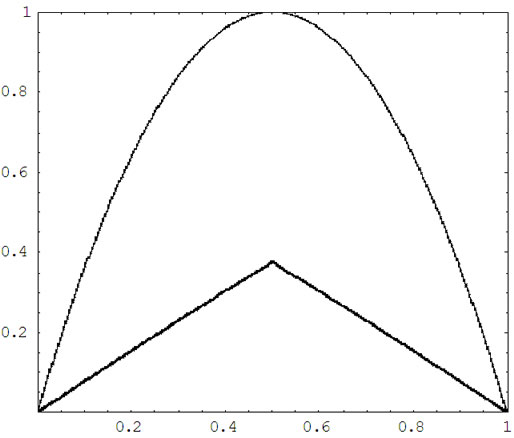
CPU Time Used: 2044.63 Second; Number of Total Subdivisions: 3301; Number of Total Pixels: 3884.
Figure 1. Voronoi diagram of two algebraic Curves (simple case)
图1. 两条代数曲线的Voronoi图(简单情形)
例2:两条代数曲线分别为一条星形线
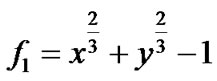 和一个圆
和一个圆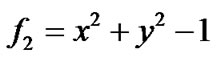 ,在平面区域
,在平面区域
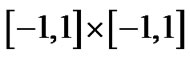 内的部分。星形线是6次曲线,相对上面例1而言,稍微复杂一些。图2是计算结果:总的CPU运行时间为11,094.1秒,总的细分次数是6763次,包括两条代数曲线构成的2维形体和它们的Voronoi图在内的总的像素是8288个。
内的部分。星形线是6次曲线,相对上面例1而言,稍微复杂一些。图2是计算结果:总的CPU运行时间为11,094.1秒,总的细分次数是6763次,包括两条代数曲线构成的2维形体和它们的Voronoi图在内的总的像素是8288个。
例3:三条代数曲线分别为圆弧
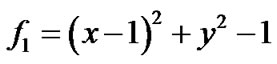 ,
,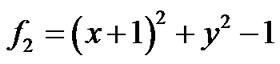 ,
,
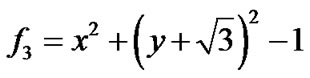 ,在平面区域
,在平面区域
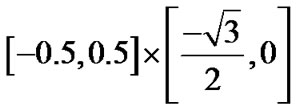 内的部分。图3是计算结果:总的CPU运行时间为40,181.2秒,总的细分次数是14,432次,包括三条代数曲线构成的2维形体和它们的Voronoi图在内的总的像素是4494个。
内的部分。图3是计算结果:总的CPU运行时间为40,181.2秒,总的细分次数是14,432次,包括三条代数曲线构成的2维形体和它们的Voronoi图在内的总的像素是4494个。
例4:四条代数曲线分别是圆弧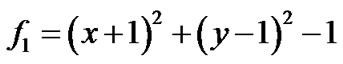 ,
,
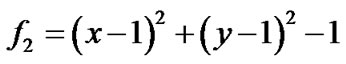 ,
,
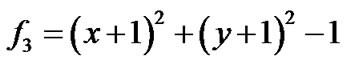 ,
,
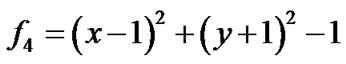 ,在平面区域
,在平面区域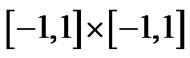 内的部分。图4是计算结果:总的CPU运行时间为32,607.9秒,总的细分次数是21,097次,包括四条代数曲线构成的2维形体和它们的Voronoi图在内的总的像素是5116个。
内的部分。图4是计算结果:总的CPU运行时间为32,607.9秒,总的细分次数是21,097次,包括四条代数曲线构成的2维形体和它们的Voronoi图在内的总的像素是5116个。
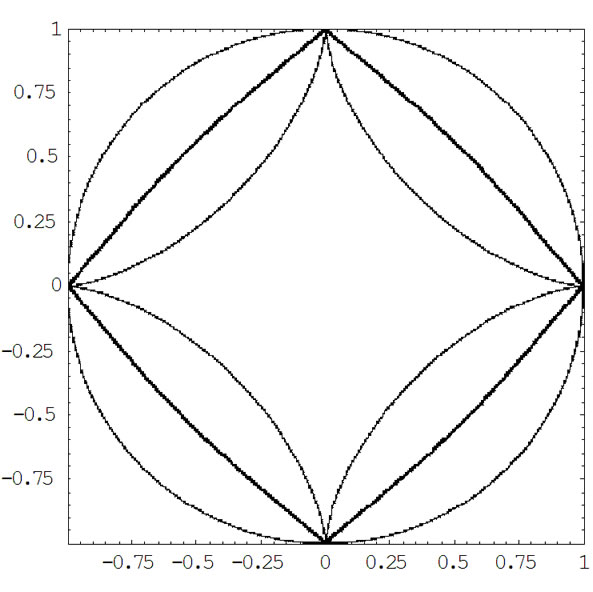
CPU Time Used: 11,094.1 Second; Number of Total Subdivisions: 6763; Number of Total Pixels: 8288
Figure 2. Voronoi diagram of two algebraic Curves (complex case)
图2. 两条代数曲线的Voronoi图(复杂情形)
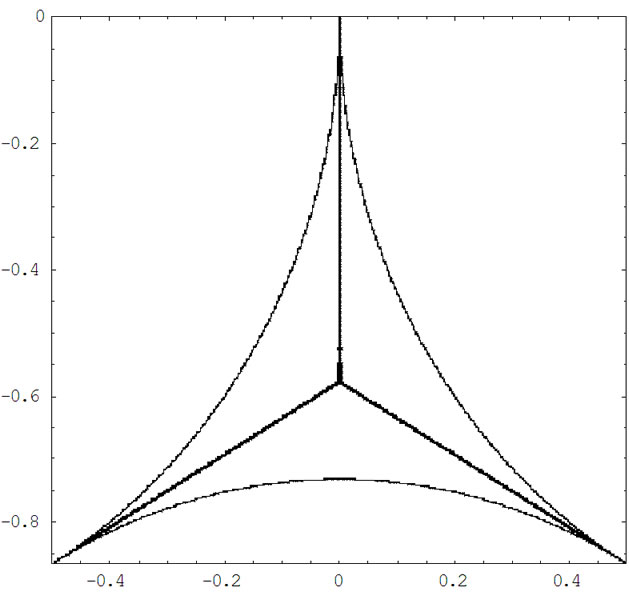
CPU Time Used: 40,181.2 Second; Number of Total Subdivisions: 14,432; Number of Total Pixels: 4494
Figure 3. Voronoi diagram of three algebraic Curves
图3. 三条代数曲线的Voronoi图
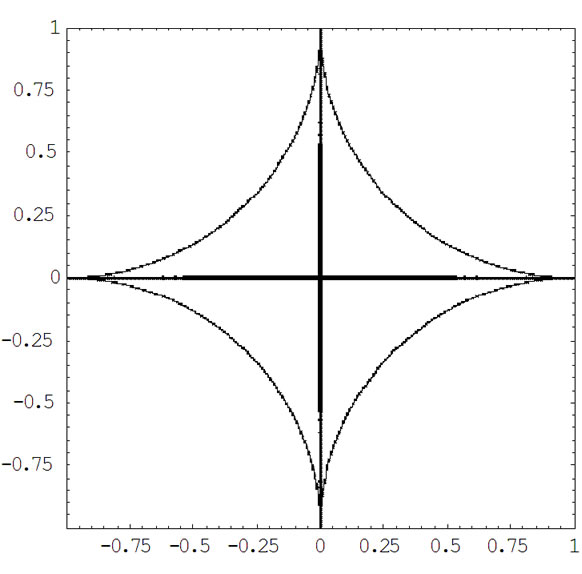
CPU Time Used: 32,607.9 Second; Number of Total Subdivisions: 21,097; Number of Total Pixels: 5116
Figure 4. Voronoi diagram of four algebraic Curves
图4. 四条代数曲线的Voronoi图
4. 结论
从上面四个实例可以看出,本文提出的算法可以准确地计算出以平面代数曲线为边界的二维图形的Voronoi图。然而我们也注意到本算法得到的是一个包含Voronoi图的像素点的集合,由于区间算术的保守性,有些邻近Voronoi图但是不应包含于Voronoi图的像素点有可能会由于无法排除而被保留了下来,这使得所得到Voronoi图的图像比实际要粗一些。此外本算法本质上是一个基于像素级操作的算法,虽然借助于于四叉树和区间算术进行了加速,但运算速度仍然比较慢。如何对本算法得到的Voronoi图进行细化以及进一步提高运算速度是我们下一步要做的工作。
5. 致谢
本文受国家自然科学基金(61070126, 61070135)和浙江省自然科学基金(Y1100837)资助。
参考文献 (References)
[1] 周培德. 计算几何—算法分析与设计[M]. 北京: 清华大学出版社, 2000: 146-216.
[2] F. P. 普雷帕拉塔, M. I. 沙莫斯. 计算几何导论[M]. 北京: 科学出版社, 1990: 226-277.
[3] 代晓巍, 李树军, 刘晓红. Voronoi图增点构造算法研究[J]. 测绘工程, 2007, 16(1): 19-22.
[4] 王新生, 刘纪远, 庄大方, 毋河海, 姜友华. 一种新的构建Voronoi图的栅格方法[J]. 中国矿业大学学报, 2003, 32(3): 293-296.
[5] 李成名, 陈军. Voronoi图生成的栅格算法[J]. 武汉测绘科技大学学报, 1998, 23(3): 208-210.
[6] 蔡强. 限定Voronoi网格剖分的理论及应用研究[M]. 北京: 北京邮电大学出版社, 2010: 5-6.
[7] 张友会, 浅野哲夫, 小保方幸次. 关于一般图形Voronoi图的近似构造法的研究[J]. 数值计算与计算机应用, 2002, 9(3): 217-225.
[8] Q. D. Li, J. Tian. 2D piecewise algebraic splines for implicit modeling. ACM Transactions on Graphics, 2009, 28(2): 1-13.
[9] R. E. Moore. Interval analysis. Englewood Cliffs: Prentice-Hall, 1966.
[10] H. H. Shou, H. W. Lin, R. Martin, and G.-J. Wang. Modified affine arithmetic is more accurate than centered interval arithmetic or affine arithmetic. Lecture Notes in Computer Science, 2003, 2768: 355-365.