Advances in Porous Flow
Vol.2 No.1(2012), Article ID:530,8 pages DOI:10.4236/apf.2012.21001
Advance in Lattice Boltzmann Method Applied in Direct Methanol Fuel Cell*
Department of Physics, Zhejiang Normal University, Jinhua
Email: #ysyou@zjnu.cn
Received: Nov. 25th, 2011; revised: Dec. 20th, 2011; accepted: Dec. 21st, 2011
ABSTRACT:
The development of lattice Boltzmann method numerical simulation was reviewed in the article for the direct methanol fuel cell (DMFC). The up-to-the-minute progress of the lattice Boltzmann method applied in multiphase flow, mass and heat transfer and electrochemical reactions in the fuel cells was described in detail. As a computational fluid dynamic method, the lattice Boltzmann method is an effective and efficient numerical scheme to analyze the performance of the fuel cell. The numerical simulations performed better understanding of the complex phenomena of fuel cells. These processes were needed for optimum call design. The latest research development was also reviewed in the article. At the same time, the deficiency of the present model was pointed out.
Keywords: Lattice Boltzmann Method; Direct Methanol Fuel Cell; Polymer Electrolyte Membrane Fuel Cell
直接甲醇质子交换膜燃料电池的格子Boltzmann 方法研究进展*
苏卫卫,许友生#
浙江师范大学物理系,金华
Email: #ysyou@zjnu.cn
摘 要:
综述了用格子Boltzmann方法模拟直接甲醇质子交换膜燃料电池的研究进展,具体介绍了利用格子Boltzmann方法模拟燃料电池中的多相流,传热传质和电化学反应过程等的最新进展,认识到格子Boltzmann方法作为一种计算流体力学的介观模拟方法,是一种有效的分析燃料电池性能的数值方法,通过数值模拟可以更好地了解电池的复杂物理化学过程,为优化电池性能提供更充分的理论依据。文章还对研究最新进展予以简单评述,同时指出了目前研究过程中所建模型存在的不足。
收稿日期:2011年11月25日;修回日期:2011年12月20日;录用日期:2011年12月21日
关键词:格子Boltzmann方法;直接甲醇燃料电池;质子交换膜燃料电池
1. 引言
随着社会的发展和人口的增长,能源消耗和环境污染成为一个严峻的社会问题,如何实现可持续发展,成为人类面临的重大问题。要从根本上解决能源危机,这就需要实现从传统能源到新型能源的转型,人类对未来能源的要求应该是清洁无污染,效率高,经济安全和价格低廉。
燃料电池是一种可以直接将燃料中的化学能转化为电能,能量转化效率高,环境友好型的电化学装置。直接甲醇燃料电池(DMFC)属于燃料电池的一种,使用甲醇,水和氧气作为燃料。DMFC具有一般的燃料电池特性外,还具有很多优势,如可在室温快速启动,能量密度高,系统简洁,无电解液流失等。
在燃料电池内发生很多物理化学现象,同时涉及到传质、传热、多孔介质、多组分、多相、动量和电化学反应。为了了解这些耦合的物理化学过程,分析电池材料参数和特定电池设计对电池性能的影响,更好地优化燃料电池系统,国内外许多研究工作组进行了实验和数值模拟研究。但是由于燃料电池中的环境是高效反应的,在电池运行时对其直接进行测量难度非常大,所以数值模拟成为最常用的研究手段。Inoue等对质子交换膜燃料电池气体扩散层中的两相流进行数值研究[1],林鸿等对质子交换膜燃料电池进行了三维数值模拟[2],此外像Kulikovsky[3],Ge和Liu[4],Xu[5]等对燃料电池中的各个结构进行了数值模拟。
格子Boltzmann方法作为计算流体的一种新工具,可以应用到多孔介质流[6,7]、化学反应流[8]、磁流体[9]、非牛顿流体[10-12]、多相多质流[13-19]等许多领域。格子Boltzmann方法与其他传统数值方法相比,具有并行性能好,物理图像清晰,程序易于实施和边界处理简单等优点,尤其在解决复杂几何结构的问题时有很大优势。因此,受到许多国内外学者的关注[20]。Joshi等利用格子Boltzmann方法模拟固体氧化物燃料电池中的多组分气体输运现象[21];Tabe等利用格子Boltzmann方法研究燃料电池中气体流管道中的两相流[22],还有许多数值研究者利用格子Boltzmann方法模拟不同的运行参数对燃料电池的影响,例如Fei等[23],Hao和Cheng[24],Park等[25]和Niu等[26]。
2. 直接甲醇燃料电池的基本工作原理和结构
直接甲醇质子交换膜燃料电池主要包括极板、多孔扩散层和膜电极(MEA),其中质子交换膜是整个电池系统的核心部分。直接甲醇燃料电池的基本工作原理如图1所示。
甲醇水溶液在阳极流道流动的过程中,穿过阳极扩散层到达阳极催化层,同时,空气(氧气)在阴极流道逐渐向阴极扩散层渗透到达阴极催化层。在阳极催化层甲醇和水反应生成CO2,氢离子并释放出电子。质子通过电解质膜到达阴极催化层,电子由外电路到达阴极催化层。在阴极催化层质子和电子与氧气反应生成水。反应式为:
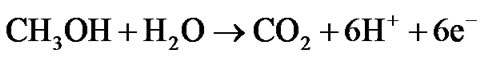 (1)
(1)
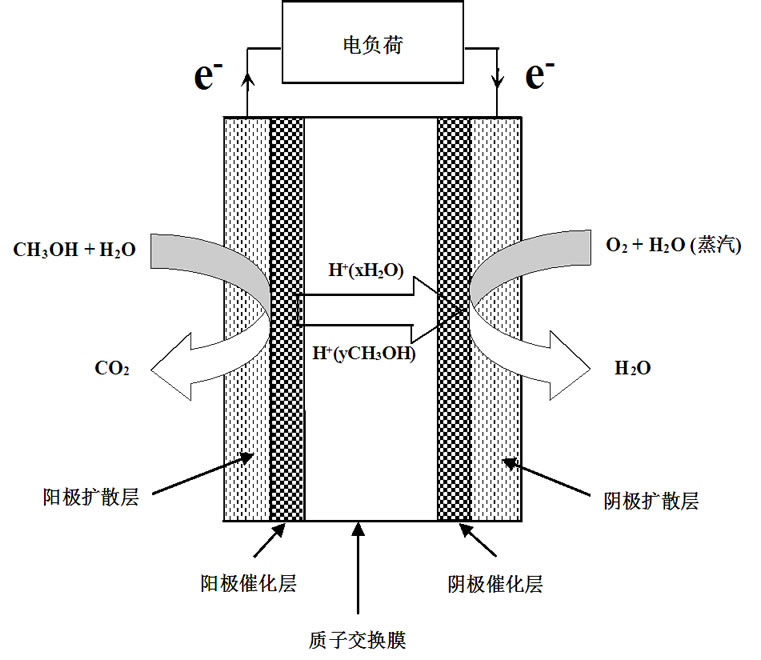
Figure 1. Schematic view of the DMFC[27]
图1. DMFC工作原理示意图[27]
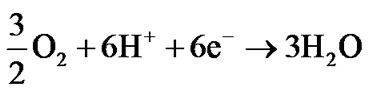 (2)
(2)
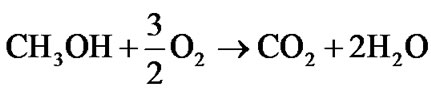 (3)
(3)
由以上反应式可知,直接甲醇燃料电池中的阴极反应跟质子交换膜燃料电池完全一样,在工作过程中电池中的游动离子也仅为质子,因此,阴极催化剂均为Pt/C,电解质膜也都为Nafion膜。
3. 直接甲醇质子交换膜燃料电池的格子 Boltzmann方法数值模拟
3.1. 格子Boltzmann方法方程体系
3.1.1. 宏观控制方程
在计算流体力学模拟中直接甲醇燃料电池阳极和阴极的流场和组分浓度是一样的,下面会分别给出模型的控制方程。
质量守恒方程:
 (4)
(4)
动量守恒方程:
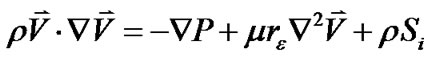 (5)
(5)
rε表示多孔介质的修正系数。
物料守恒方程:
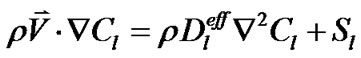 (6)
(6)
l表示阳极的甲醇,水,CO2和阴极的O2,水蒸气。Cl为组分l的摩尔浓度,Sl为化学组分在电化学反应过程中质量产生或消耗的速率。

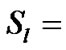 (7)
(7)
式中,n为组分l反应的得失电子数,s为反应的化学计量系数,j为体积反应率。
电化学反应率:
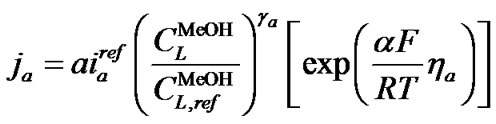 (8)
(8)
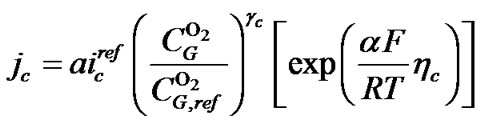 (9)
(9)
式中,下标a和c表示阳极和阴极,airef为参考交换电流密度,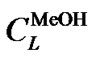 为甲醇摩尔浓度,
为甲醇摩尔浓度,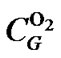 为氧气摩尔浓度,
为氧气摩尔浓度,![]() 为参考甲醇摩尔浓度,
为参考甲醇摩尔浓度,![]() 为参考氧气摩尔浓度,γ和α分别为浓度参数和传递系数,η为过电位,T为温度,R为气体常数。
为参考氧气摩尔浓度,γ和α分别为浓度参数和传递系数,η为过电位,T为温度,R为气体常数。
3.1.2. 格子Boltzmann方程
考虑了外力的流场的格子Boltzmann方程为:
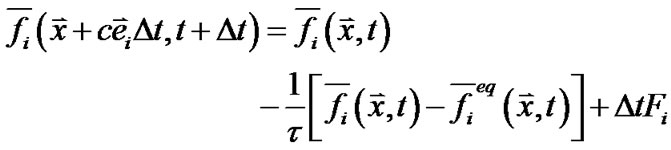 (10)
(10)
![]() 是t时刻处于
是t时刻处于![]() 位置,速度为
位置,速度为 的粒子的体平均密度分布函数,τ是无量纲弛豫时间,
的粒子的体平均密度分布函数,τ是无量纲弛豫时间,![]() 是时间的增量。体平均平衡态分布函数
是时间的增量。体平均平衡态分布函数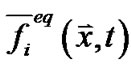 定义为
定义为
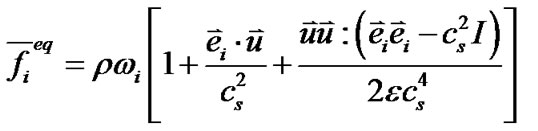 (11)
(11)
![]() 为权重,
为权重,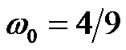 ,当
,当 时,
时,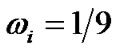 ,当
,当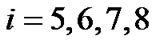 时,
时,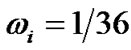 ,
,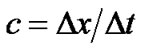 为格子速度,
为格子速度,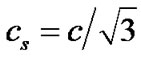 ,
,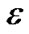 为多孔介质的孔隙度。
为多孔介质的孔隙度。
方程(10)中的外力项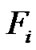 定义为[28,29]:
定义为[28,29]:
 (12)
(12)
采用D2Q9格子Boltzmann模型,离散的速度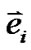 为,
为,
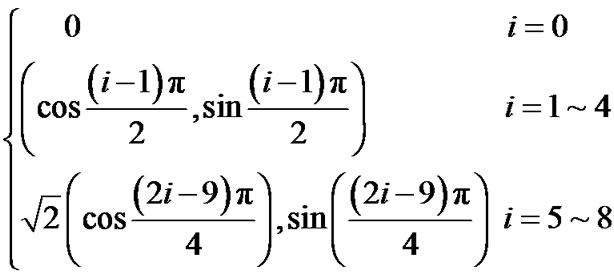
 (13)
(13)
体平均密度和速度分别定义为,
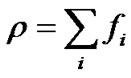 ,
, 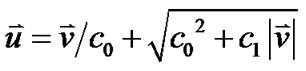 ,
,
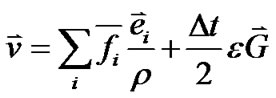 (14)
(14)
其中,
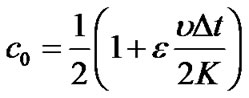 ,
, 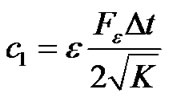 (15)
(15)
与流场分布函数不同,浓度场的格子Boltzmann方程分布函数为
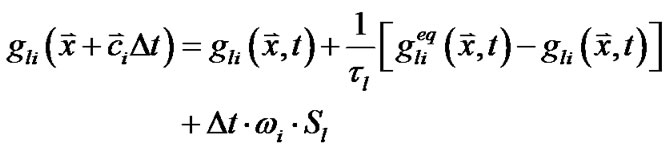 (16)
(16)
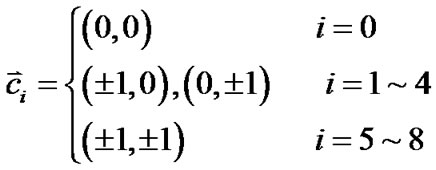 (17)
(17)
相应的平衡态分布函数为[30-32]:
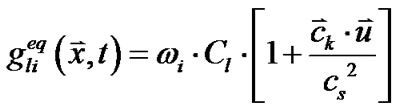 (18)
(18)
方程(10)和(16)中的弛豫时间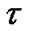 和
和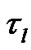 分别定义为
分别定义为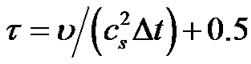 和
和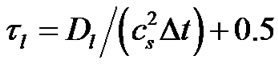 ,
,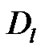 为组分l的扩散系数。
为组分l的扩散系数。
3.1.3. 边界处理
电池内流场和浓度场采用相同的边界处理格式,我们以流场为例来说明边界处理方式。如图2所示,流体节点以实心圆圈表示,增加的虚拟流体节点以空心圆圈表示,考虑均匀网格(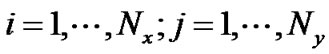 )覆盖流场,水平方向采用非平衡外推格式,竖直方向采用周期性边界处理格式。由此,需要在竖直方向上增加两层网格(
)覆盖流场,水平方向采用非平衡外推格式,竖直方向采用周期性边界处理格式。由此,需要在竖直方向上增加两层网格(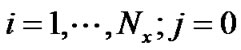 )和(
)和(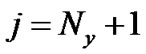
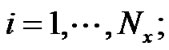 ),代表虚拟流体节点。周期性边界处理格式表达为
),代表虚拟流体节点。周期性边界处理格式表达为
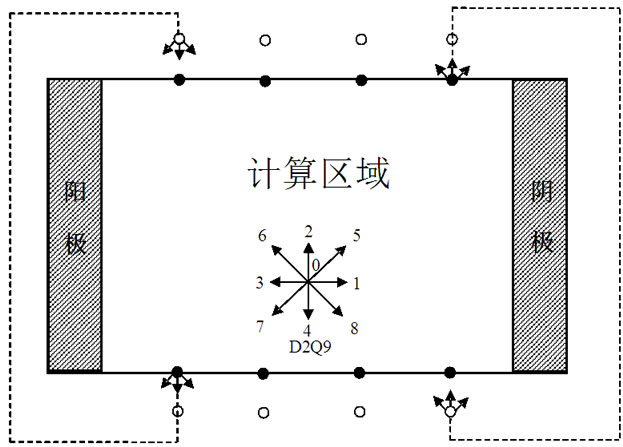
Figure 2. Schematic view of the periodic boundary
图2. 周期性边界处理示意图
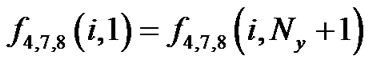 (19)
(19)
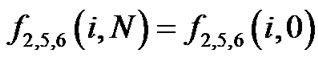 (20)
(20)
式中,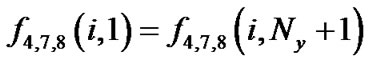 表示虚拟流体节点
表示虚拟流体节点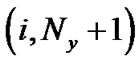 上的分布函数
上的分布函数![]() 、
、![]() 和
和![]() 与流体节点
与流体节点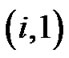 上的分布函数
上的分布函数![]() 、
、![]() 和
和![]() 相等。
相等。
水平方向采用非平衡外推格式,考虑碰撞过程,边界节点O点的分布函数可以表示为
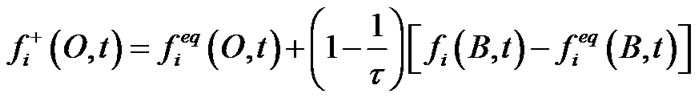 (21)
(21)
式中,节点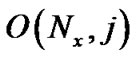 为边界节点,节点
为边界节点,节点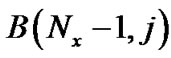 与O点为相邻流体节点。
与O点为相邻流体节点。![]() 为碰撞后的分布函数。
为碰撞后的分布函数。
3.1.4. 直接甲醇质子交换膜燃料电池的格子 Boltzmann方法数值模拟研究现状
燃料电池运行时涉及到多孔介质流、热质传递、电化学反应和多组分多相流等复杂物理过程。采用格子Boltzmann方法模拟多相流,可以方便地描述出相与相之间的相互作用;模拟多孔介质流,可以直接描述孔隙内的流体流动。格子Boltzmann方法作为一项重要的数值计算方法,一直都在发展,在许多领域取得了开拓性进展[33-38]。
在直接甲醇燃料电池中,甲醇水溶液在阳极催化层反应生成CO2,如果CO2气体大量聚集会堵塞流道,降低燃料电池性能,所以如何去除CO2气泡是人们较为关注的问题。Fei等对DMFC阳极流道中的甲醇溶液和CO2气体两相流动建立了物理模型如图3,并用热格子Boltzmann模型(TLBM)对阳极微管道中的相流进行了数值模拟,然后用商业软件对结果进行了验证,主要目的是得到一个高效的计算方法来解决这一
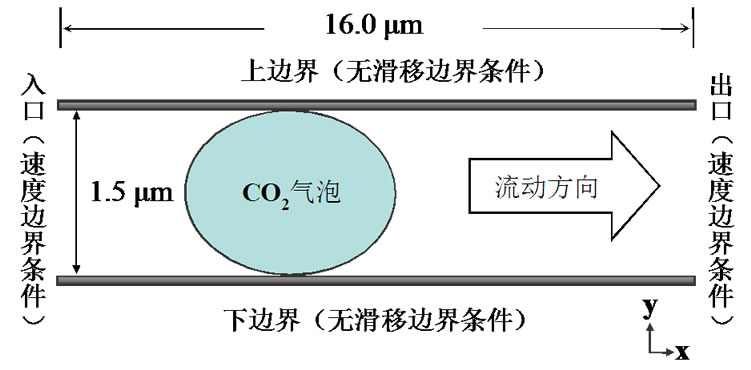
Figure 3. Schematic diagram of the simulation domain of the bubbly thermal flow in a microchannel in which x-axis is the flow direction and y-axis is opposite to the gravity. The microchannel is 16.0 um long and 1.5 um high. No-slip boundary conditions are applied at the upper and bottom walls, while velocity boundary conditions are imposed at the inlet and exit of the microchannel
图3. 微管道中气泡热流的计算区域示意图,x轴是流动方向,y轴是重力的反方向。微管道长16.0 um,高1.5 um。上表面和下表面利用无滑移边界条件,管道的进口和出口施加速度边界条件[35]问题[23]。研究表明:气泡的尺寸随着壁面温度的增加而减小,在微管道中气泡尺寸的改变对气泡的流动性有很明显的影响,小气泡相比较大气泡流动性比较强,也就是说在壁面温度高的微管道中小气泡移动较快。关于气泡输运速度和壁面温度之间的关系,TLBM和VOF(volume of fluid)两种数值方法得到了一致的结论,就是即使气泡在入口速度为0,但只要沿着管道有温度梯度,气泡可以在水平微管道中自动地移动,气泡的移动速度随着温度梯度的增加而增加。模拟结果对DMFC中CO2去除技术的研究可以起到积极的作用,同时证明了热格子Boltzmann方法模拟微管道中气泡热流的可行性和高效性。但在这一工作中,他们把DMFC阳极流道看作是微管道进行建模,所建的物理模型只是对DMFC阳极流道的一个简化,而且所建模型没有能够与扩散层及膜当中的传热传质过程较好地结合起来,没有全面地描述流道中的流场形式。
Tabe等用格子Boltzmann方法模拟了质子交换膜燃料电池阴极中反应物和产物的两相流,研究了水和气体混合流的动力学特征[39]。在处理Poisson方程的离散,节点处的压强边界和入口处的粒子分布函数时,改进了格子Boltzmann方法计算过程使之能够扩展应用到气体扩散层这一多孔介质中。结果表明:1) 在质子交换膜燃料电池两相流中,考虑毛细管力,粘力和惯性力的作用,LBM可以模拟毛细管数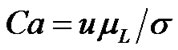 对液态水流动的影响。2) 通过对有无气体流道两种气体扩散层中的两相流模拟,得到气体流道和气体扩散层的润湿性对两相流的影响较大,进一步说明可以通过控制气体流道和多孔扩散层的润湿性来得到液态水和空气的最佳分布,从而使催化层的氧气供应充分。可以看出,文章在研究液态水和空气之间的相互作用对燃料电池性能影响的现象中,体现了考虑整个系统物理性质的格子Boltzmann方法和适当地选择边界条件的优越性。但是他们的建模没有包含阳极,催化层和膜,而且模拟中设定温度为恒温,是一个严重的模拟局限。温度分布的不同会对水的相变数量有影响,因此不能考虑带有相变的物理现象。
对液态水流动的影响。2) 通过对有无气体流道两种气体扩散层中的两相流模拟,得到气体流道和气体扩散层的润湿性对两相流的影响较大,进一步说明可以通过控制气体流道和多孔扩散层的润湿性来得到液态水和空气的最佳分布,从而使催化层的氧气供应充分。可以看出,文章在研究液态水和空气之间的相互作用对燃料电池性能影响的现象中,体现了考虑整个系统物理性质的格子Boltzmann方法和适当地选择边界条件的优越性。但是他们的建模没有包含阳极,催化层和膜,而且模拟中设定温度为恒温,是一个严重的模拟局限。温度分布的不同会对水的相变数量有影响,因此不能考虑带有相变的物理现象。
Hao和Cheng利用多相自由能格子Boltzmann方法模拟了质子交换膜燃料电池中穿过疏水性气体扩散层微孔的水滴的形成,并且研究了水滴在气体剪切力作用下在气体扩散层表面的运动情况[24]。呈现了水滴的出现,生长,脱落和运动过程,研究了在气体流动速度和气体扩散层表面润湿性影响下的脱落水滴的尺寸和去除管道中水滴的时间。结果表明在疏水性强的气体扩散层表面上,气体流速越大,水滴越容易去除。此外,利用基于力平衡的解析模型求解了水滴脱落尺寸,结果跟LBM模拟的结果相一致。说明LBM是一种有效的工具来研究PEMFC气体流道的水输运现象。
质子交换膜燃料电池的电极通常是由碳布或碳纸构成的多孔介质。Park等用格子Boltzmann方法模拟了流体在多孔电极中的流动[40],计算了多孔介质的有效渗透率,并与文献[41]中的解析解作对比,结果一致如图4。他们还建立了三维纤维多孔介质模型来研究纤维屑的排列方向对有效渗透率的影响,结果表明平行与平均流动方向的有效渗透率比垂直于平

Figure 4. Comparison of the effective permeability between the LB simulation (circles) and the lubrication model(square), as a function of the dimensionless tow permeability; the nominal porosity(εnom) of porous medium is 0.4
图4. LB模拟和lubrication模型的有效渗透率比较[40]
均流动方向的有效渗透率大很多,接近于两倍。
Niu等用多相,多弛豫时间格子Boltzmann模型模拟研究了质子交换膜燃料电池系统气体扩散层中的水气输运过程[26]。这一模型基于平均场扩散界面理论,能够处理大密度比率和不同粘性下的多相流。无滑移边界和润湿边界分别采用标准的反弹边界条件和近似平均方法进行处理,能够详细地描述气体扩散层中的液气输运。不像大多数的格子Boltzmann方法是基于Bhatnagar-Gross-Krook碰撞项,文中模型采用与粘性无关的速度场,这对模拟不同粘性共存的多相流是非常重要的。通过模拟在润湿壁面上的静电液滴,并且与理论计算相比较,验证了这一模型的正确性。然后,文章模拟了质子交换膜燃料电池系统气体扩散层中的水气流动,研究了在不同条件下与饱和度有关的输运性质,模拟结果跟文献中的数值模拟和实验得到的结果相吻合[42,43]。
质子交换膜燃料电池的气体扩散层是由碳布或碳纸构成的多孔介质。在有关质子交换膜燃料电池的文献中一般把气体扩散层作为渗透率为常量的各向同性多孔介质来建模。实际上,纤维的排列方向造成的碳纸的各向异性影响多孔介质的渗透率。Park和Li通过格子Boltzmann方法解决了质子交换膜燃料电池各向异性气体扩散层中的多相流现象[25]。把碳布和碳纸的各向异性孔隙结构分为空隙空间和孔隙空间进行建模,利用Stokes/Brinkman公式求解,从各种显微图像得到空隙空间和不可渗透的纤维分布。计算得到的多孔介质的渗透性和文献[44]中的实验数据相一致。各种纤维分布的模拟结果说明纤维的排列方向影响介质的渗透率。模拟多相流的格子Boltzmann模型是基于多组分格子Boltzmann模型和粒子间相互作用力的结合,该模型成功地模拟了在多孔介质中液滴运动的复杂不稳定性,为质子交换膜燃料电池多孔电极中液态水聚集和去除机理的研究提供了有力的工具。
在质子交换膜燃料电池阴极中,发生着各种化学、物理、电学、电化学等过程,反应物传递速度慢,电化学反应速率低是影响PEMFC性能的主要因素,需要从孔隙尺度来深入地研究这些过程。陈黎等采用格子Boltzmann方法直接从介观层次模拟了质子交换膜燃料电池阴极催化层的传质和电化学反应过程[45]。建立了理想二维规则模型,为了验证结果的正确性,模拟所得的极化曲线和文献[46]的极化曲线吻合较好。用电镜扫描PEMFC阴极催化层,处理图象得到了一个实际二维计算模型。利用格子Boltzmann方法进行模拟,得到了二维的氧气浓度和电势分布。表明利用格子Boltzmann方法计算分析PEMFC阴极催化层中传递和电化学反应是行之有效的。传统的宏观模型考虑象曲折度、孔隙率、催化层组分和催化层厚度等宏观参数对燃料电池催化层性能的影响,这样建立的模型跟实际结构相比较有一定的差别,因此不能充分说明催化层结构对燃料电池性能的影响。而LBM直接基于实际结构对传质和电化学反应过程进行研究,不依赖于曲折度、孔隙率这些宏观参数。
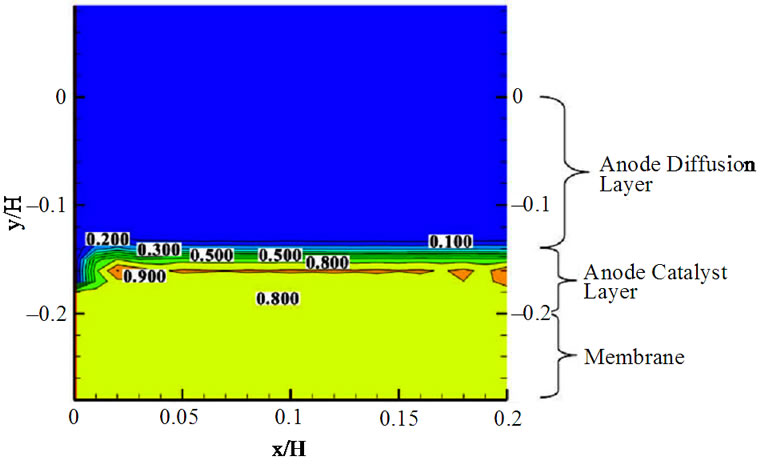
上面介绍了用格子Boltzmann方法模拟微管道,气体扩散层,阴极催化层,但仅仅局限于燃料电池的某一组件,没有综合考虑电池中发生的传质和流动,基于燃料电池整体的模拟无疑会得到更完整、可靠的信息。Delavar等用格子Boltzmann方法,采用D2Q9模型对DMFC全电池进行数值模拟,计算区域包括阳极流道,阳极催化层,阳极扩散层,质子交换膜,阴极流道,阴极催化层和阴极扩散层[47]。这一模型通过模拟反应物和生成物分别在空流道和多孔流道中的流动模式和浓度场分布来研究电池的性能。从图5可以看出,在多孔介质区域流场改变并且速度减小,流体在阴极流道的速度比在阳极流道快。在模拟流场时,由于这种速度的不同,存在两个流道交界面的收敛问题,所以阳极和阴极采用不同的分布函数。从图6可以看出,在反应催化层周围,反应物的浓度减小,生成物的浓度增大。计算结果得到了合理的流场分布和CO2及甲醇浓度分布,文章还得到了在一定操作条件
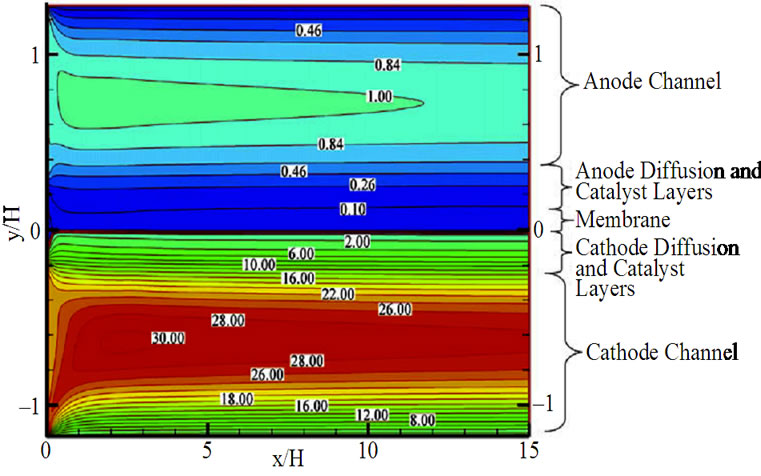
Figure 5. Velocity contours (U/Umax-anode) for all seven parts of DMFC[47]
图5. DMFC的速度分布(U/Umax-anode)[47]
 (a)
(a)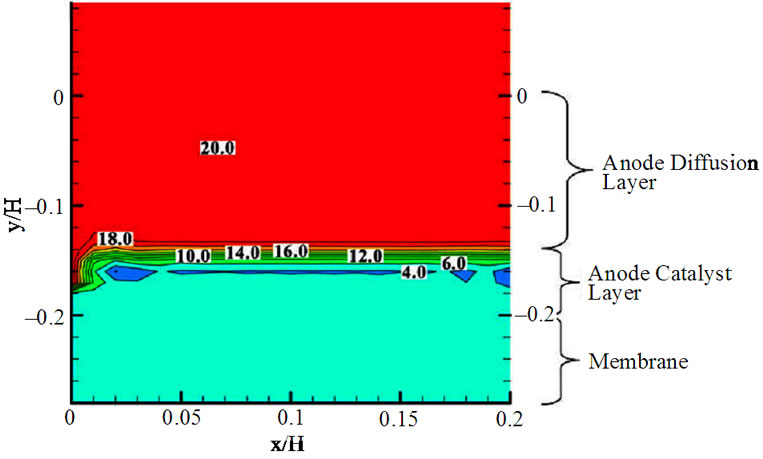 (b)
(b)
Figure 6. Instantaneous carbon dioxide and methanol concentration contours (kgm–3) for anode channel, diffusion and catalyst layers, membrane
图6. 阳极流道,扩散层,催化层和质子交换膜上的瞬时CO2(a)和甲醇(b)浓度分布[47]
下的极化曲线,我们可以在此基础上进一步讨论燃料电池的结构参数和操作条件对电池性能的影响。结果表明,这一模型能够比较精确地研究DMFC的流动模式和性能,为进一步的研究打下良好基础。
4. 用格子Boltzmann方法模拟直接甲醇 质子交换膜燃料电池存在的问题
1) 研究人员用格子Boltzmann方法研究了两相流现象,但是在阴极伴随有水的蒸发和冷凝过程,人们均忽略了水的相变过程,没有很好地考虑相变与传热之间的相互影响,没有综合考虑到催化层反应动力学对传质的影响以及流道中水蒸发和凝结过程中吸收和释放的潜热的影响。阴极淹没和膜的干涸等现象都是伴随水的相变过程而产生的一些非正常现象,如果考虑了相变过程进行深入研究将会是十分有意义的。
2) 由于进行三维模拟时计算复杂性等因素,进行三维数值模拟的工作相对较少,建立的模型大多数都是二维的,而且进行了简化,忽略了电池内的一些特殊情况,不能详细地描述电池内的传质传热和电化学反应过程。
3) 人们把格子Boltzmann方法数值模拟的研究重点放在了两相流上面,忽略了工作温度,空气压力,甲醇水溶液浓度,流量,电池结构,运行工况等参数对电池性能的影响。例如,当电池作为交通工具等电源时,经常处于变工况的工作状态下,了解电池的动态特性对优化电池的性能也是十分重要的。
5. 结束语
格子Boltzmann方法作为一种计算流体力学的方法,应用在许多传统模拟方法不能胜任的领域,比如多相流,复杂几何结构和伴随有化学反应的流动过程。人们对直接甲醇质子交换膜燃料电池建立不同的模型,利用格子Boltzmann方法对其进行模拟计算,涉及多孔介质,微管道,热流,多相流,还有直接对DMFC整体进行建模。通过数值模拟,详细揭示了电池内复杂流动结构、传热传质过程、电化学反应动力学及其对电池性能的影响,可以为优化燃料电池的性能提供有力的理论依据,也更具有实际应用价值。但同时为了更进一步深层次的了解燃料电池,提高其性能,要综合考虑相变和传热、传质间的相互影响,催化层内的电化学反应动力学和传质、电荷传递间的耦合作用。因此,我们还需要结合相变,两相流和电化学反应等建立先进的燃料电池综合模型,利用格子Boltzmann方法的优势对其进行数值模拟。
6. 致谢
感谢给予转载和引用权的资料、图片、文献、研究思想和设想的所有者。
参考文献 (References)
[1 G. Inoue, T. Yoshimoto, Y. Matsukuma, et al. Development of simulated gas diffusion layer of polymer electrolyte fuel cells and evaluation of its structure. Journal of Power Sources, 2008, 175(1): 145-158.
[2] 林鸿, 陶文铨. 质子交换膜燃料电池的三维数值模拟[J]. 西安交通大学学报. 2008, 42(1): 41-45.
[3] A. A. Kulikovsky, J. Divisek and A. A. Kornyshev. Two-dimensional simulation of direct methanol fuel cell—A new (embedded) type of current collector. Journal of the Electrochemical Society, 2000, 147(3): 953-959.
[4] J. Ge, H. Liu. A three-dimensional mathematical model for liquid-fed direct methanol fuel cells. Journal of Power Sources, 2006, 160(1): 413-421.
[5] C. Xu, A. Faghri, X. Li, et al. Methanol and water crossover in a passive liquid-feed direct methanol fuel cell. International Journal of Hydrogen Energy, 2010, 35(4): 1469-1777.
[6] G. Tang, W. Tao and Y. He. Gas slippage effect on microscale porous flow using the lattice Boltzmann method. Physical Review E, 2005, 72(5): Article ID 056301.
[7] Z. L. Guo, T. S. Zhao. Lattice Boltzmann model for incompressible flows through porous media. Physical Review E, 2002, 66(32B): 036301-036304.
[8] S. Chen, S. P. Dawson and G. D. Doolen, et al. Lattice methods and their applications to reacting systems. Computers and Chemical Engineering, 1995, 19(6): 617-646.
[9] S. Chen, H. D. Chen, D. Martinez, et al. Lattice Boltzmann model for simulation of magnetohydrodynamics. Physical Review Letters, 1991, 67(27): 3776-3779.
[10] N. Rakotomalala, D. Salin and P. Watzky. Simulations of viscous flows of complex fluids with a Bhatnagar, Gross, and Krook lattice gas. Physics of Fluids, 1996, 8(11): 3200-3202.
[11] E. S. Boek, J. Chin and P. V. Coveney. Lattice Boltzmann simulation of the flow of non-Newtonian fluids in porous media. International Journal of Modern Physics B, 2003, 17(1-2): 99-102.
[12] S. Gabbanelli, G. Drazer and J. Koplik. Lattice Boltzmann mothod for non-Newtonian (powerlaw) fluids. Physical Review E, 2005, 72: Article ID 046312.
[13] D. Grunau, S. Chen and K. Eggert. A Lattice Boltzmann model for multiphase fluid-flows. Physics of Fluids, 1993, 5: 2557- 2562.
[14] A. Gunstensen, D. Rothman, S. Zaleski, et al. Lattice Boltzmann model of immiscible fluids. Physical Review E, 1991, 43(8): 4320-4327.
[15] 李维仲, 李爽. 用格子Boltzmann方法模拟液滴合并过程[J]. 热科学与技术, 2007, 6(3): 379-393.
[16] M. Swift, E. Orlandini, W. Osborn, et al. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Physical Review E, 1996, 54: 5041-5052.
[17] T. Inamuro, T. Ogata, S. Tajima, et al. A lattice Boltzmann mothod for incompressible two-phase flows with large density differences. Journal of Computational Physics, 2004, 198(2): 628- 644.
[18] L. Luo. Theory of the lattice Boltzmann mothod: Lattice Boltzmann models for nonideal gases. Physical Review E, 2000, 62 (4): 4982.
[19] X. He, S. Chen and R. Zhang. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability. Journal of Computational Physics, 1999, 152(2): 642-663.
[20] C. L. Tien, A. Majumdar, V. P. Carey, et al. Molecular and microscal transport phnomena: A report on the 2nd US Japan joint seminar, Santa Barbara, California, 1996. Microscale Thermophysical Engineering, 1997, 1(1): 71-84.
[21] A. S. Joshi, K. N. Grew, A. A. Peracchio, et al. Lattice Boltzmann modeling of 2D gas transport in a solid oxide fuel cell anode. Journal of Power Sources, 2007, 164(2): 631-638.
[22] Y. Tabe, T. Ochi, K. Kikuta, et al. Numerical simulation of liquid water behavior in separator-channels in PEMFC using LBM. Proceedings of 3rd International Conference on Fuel Cell Science Engineering and Technology, Ypsilanti, 2005: 1-6.
[23] K. Fei, T. S. Chen and C. W. Hong. Direct methanol fuel cell bubble transport simulations via thermal lattice Boltzmann and volume of fluid methods. Journal of Power Sources, 2010, 195(7): 1940-1945.
[24] L. Hao, P. Cheng. Lattice Boltzmann simulations of liquid droplet dynamic behavior on a hydrophobic surface of a gas flow channel. Journal of Power Sources, 2009, 190(2): 435-446.
[25] J. Park, X. Li. Multi-phase micro-scale flow simulation in the electrodes of a PEM fuel cell by lattice Boltzmann method. Journal of Power Sources, 2008, 178: 248-257.
[26] X. D. Niu, T. Munekata, S. A. Hyodoa, et al. An investigation of water-gas transport processes in the gas-diffusion-layer of a PEM fuel cell by a multiphase multiple-relaxation-time lattice Boltzmann model. Journal of Power Sources, 2007, 172(2): 542- 552.
[27] 陈志. 直接甲醇质子交换膜燃料电池中阳极CO2去除及水、热的综合管理[D]. 东南大学, 2006.
[28] A. Cancelliere, C. Chang, E. Foti, et al. The permeability of a random medium: Comparison of simulation with theory. Physics of Fluids A, 1990, 2(12): 2085-2088.
[29] K. J. Malory, L. Furuberg, J. Feder, et al. Dynamics of slow drainage in porous media. Physical Review Letters, 68(14): 2161-2164.
[30] M. A. Delavar, M. Farhadi and K. Sedighi. Effect of the heater location on heat transfer and entropy generation in the cavity using the lattice Boltzmann Methode. Heat Transfer Research, 2009, 40(6): 521-536.
[31] A. Mezrhab, M. Jami, C. Abid, et al. Lattice-Boltzmann modelling of natural convection in an inclined square enclosure with partitions attached to its cold wall. International Journal of Heat Fluid Flow, 2006, 27(3): 456-465.
[32] A. A. Mohammad. Applied lattice Boltzmann method for transport phenomena momentum heat and mass transfer. Calgary: The University of Calgary Press, 2007.
[33] S. Chen, G. D. Doolen. Lattice Boltzmann method for fluid flows. Annual Review of Fluid Mechanics, 1998, 30(1): 329- 364.
[34] B. Chopard, P. O. Luthi. Lattice Boltzmann computations and applications to physics. Theory Computational Physics, 1999, 217: 115-130.
[35] J. R. Ho, C. P. Kuo and W. S. Jiaung. Study of heat transfer in multilayered structure within the framework of dualphaselag heat conduction model using lattice Boltzmann method. International Journal of Heat Mass Transfer, 2003, 46(1): 55-69.
[36] J. R. Ho, C. P. Kuo, W. S. Jiaung, et al. Lattice Boltzmann scheme for hyperbolic heat conduction equation. Numerical Heat Transfer B, 2002, 41(6): 591-607.
[37] R. R. Nourgaliev, T. N. Dinh, T. G. Theofanous, et al. The Lattice Boltzmann equation method: Theoretical interpretation, numerics and implications. International Journal of Multiphase Flow, 2003, 29(1): 117-169.
[38] R. G. M. VonderSman, M. H. Ernst and A. C. Berkerbosch. Lattice Boltzmann scheme for cooling of packed cut flowers. International Journal of Heat Mass Transfer, 2000, 43(4): 577- 587.
[39] Y. Tabe, Y. Lee, T. Chikahisa, et al. Numerical simulation of liquid water and gas flow in a channel and a simplifed gas diffusion layer model of polymer electrolyte membrane fuel cells using the lattice Boltzmann method. Journal of Power Sources, 2009, 193(1): 24-31.
[40] J. Park, M. Matsubara and X. Li. Application of lattice Boltzmann method to a micro-scale flow simulation in the porous electrode of a PEM fuel cell. Journal of Power Sources, 2007, 173: 404-414.
[41] F. R. Phelan, Jr., G. Wise. Analysis of transverse flow in aligned fibrous porous media. Composites, 1995, 27A: 25.
[42] H. Li, C. Pan and C. T. Miller. Pore-scale investigation of viscous coupling effects for two-phase flow in porous media. Physical Review E, 2005, 72(4): Article ID 026705.
[43] H. Chen, S. Chen and W. H. Matthaeus. Recovery of the NavierStokes equations using a lattice-gas Boltzmann method. Physical Review A, 1992, A45: 5539.
[44] J. P. Feser, A. K. Prasad and S. G. Advani. Experimental characterization of in-plane permeability of gas diffusion layers. Journal of Power Sources, 2006, 162(2): 1226-1231.
[45] 陈黎, 栾辉宝, 陶文铨. PEMFC阴极催化层的LBM模拟[J]. 电源技术, 2009, 33(9): 794-797.
[46] G. Wang, P. P. Mukherjee and C. Y. Wang. Direct numerical simulation (DNS) modeling of PEFC electrodes Part I. Random micro-structure. Electrochimica Acta, 2005, 51(15): 3151-3160.
[47] M. A. Delavar, M. Farhadi and K. Sedighi. Numerical simulation of direct methanol fuel cells using lattice Boltzmann method. International Journal of Hydrogen Energy, 2010, 35(17): 9306- 9317.
NOTES
*基金项目:国家自然科学基金10932010,11072220资助。
#通讯作者。