Advances in Porous Flow
Vol.05 No.01(2015), Article ID:14991,7
pages
10.12677/APF.2015.51001
Coalbed Methane Vertical Well Production Hydraulic Model Building
Dongmin Ma1,2, Jianfeng Qian3, Jie Wang1, Houning Liu1, Fangqing Li1
1Xi’an University of Science and Technology, Xi’an Shaanxi
2Key Laboratory of National Energy Coal and Coal Bed Methane Joint Mining Technology, Jincheng Shanxi
3Shaanxi Coalbed Methane Development Corp. Ltd., Xi’an Shaanxi
Email: mdm6757@126.com
Received: Mar. 2nd, 2015; accepted: Mar. 20th, 2015; published: Mar. 26th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In order to study the prediction model of gas production of CBM wells in the drainage process with the shortage of geological data, we calculated the transmissibility of reservoir and the conical depression influence radius of water cone by using Theis formula and Jacob formula, calculated the critical desorption pressure by using Langmuir formula and calculated the desorption radius of CBM wells by integral. We founded the simulation results and the actual production curve with a better fit degree by model building and gas production fitting of single well. The result showed that there is a linear relationship between the bottom hole pressure in different production stages and water production. The conical depression influence radius of water cone and level drawdown shows a logarithm relationship, and it shows a exponential relationship with the production time. The transmissibility and the influence radius have the greatest effect on the gas production in the objective factors.
Keywords:CBM Vertical Well, Mining Row, Influence Radius, Hydraulic Model, Gas Production
煤层气直井排采初期水力模型的建立
马东民1,2,钱建峰3,王杰1,刘厚宁1,李方晴1
1西安科技大学,陕西 西安
2国家能源煤与煤层气共采技术重点实验室,山西 晋城
3陕西省煤层气开发利用有限公司,陕西 西安
Email: mdm6757@126.com
收稿日期:2015年3月2日;录用日期:2015年3月20日;发布日期:2015年3月26日

摘 要
为研究在地质资料不足的情况下煤层气井产气量的预测模型,利用Theis公式、Jacob公式对煤层气储层的导水系数、降落漏斗影响半径进行计算,利用Langmuir公式对煤层气临界解吸压力计算,并通过积分计算煤层气井的解吸半径。通过建立大佛寺煤层气直井排采过程的水力模型,进行单井产气量模拟,结果与实际排采曲线吻合程度较好。我们发现:不同排采阶段井底压力与产水量呈线性关系;降落漏斗影响半径与液面降深呈对数关系,与排采时间呈幂指数关系;在客观因素上,导水系数、影响半径对产气量的影响最大。
关键词 :煤层气直井,排采,影响半径,水力模型,产气量

1. 引言
煤储层相对于常规天然气储层,不仅具有割理和基质孔隙的双重孔隙特征,而且由于煤岩为高泊松比、低强度的岩石[1] ,故而其排采过程与常规天然气有着很大区别。通常煤层气产出大致经历饱和水单相流、非饱和水单相流(水与不连续甲烷气体混合)和两相流(连续甲烷气体与水混合)三个阶段 [2] 。在排采过程中,由于气、水相对渗透率和影响半径的变化,以及煤储层应力敏感负效应、滑脱效应和基质收缩正效应的影响 [3] [4] ,使得煤层气排采过程中的机制模拟和有关参数的计算非常困难,而且对于不同的地区,其煤层气产出过程均有着自己的特点,应建立不同的动力模型,而在煤层气井排采初期,储层的敏感性尤为重要,直接关系到后期产气的持续时间与产量。本文利用水文地质相关模型,建立了大佛寺煤层气井排采过程中的物理参数计算模型,为今后煤层气排采过程中的地下水降落漏斗及压力梯度变化的确定提供理论依据。
2. 排采阶段划分
传统的煤层气排采过程根据相态的变化分为三个阶段 [5] - [7] ,但在对煤层气排采过程的水力模型建立时发现,仅以相态变化对煤层气井排采过程进行阶段划分,不仅不能反映煤层气井排采过程的地下条件的动态变化,而且很容易进入排采理论指导误区 [8] 。本文结合煤层气排采曲线特征与倪小明提出来的煤层气排采过程的阶段划分方案,将煤层气产出分为4个阶段(图1):1) 饱和水单相流(无气体产出)阶段;2) 非饱和水单相流(游离气产出)阶段;3) 两相流(解吸气产出)过渡阶段;4) 两相流(煤层气稳产至衰减)阶段——井筒四周压力仅在某方向缓慢传递。
煤层气排采初期,只有水的排出而无气体产出,随着排采的进行,排采水中有气体的产出,而且产出量增长速度很快,此时气体为煤储层中的游离气及溶解气;继续排采,产气量出现急剧下降现象,为过渡阶段,此阶段开始,解吸气开始产出,煤储层的速敏效果、压力负效应等因素导致产气量变化无常,从排采曲线上看为锯齿状 [9] ,煤层气井日产气量波动较大且有所下降;随着排采继续进行,产气量上升达到高峰,并稳定产期,此为煤层气井排采的稳产阶段,此时井筒四周压力几乎平稳向四周传递,到后

Figure 1. Historical production curve of DFS-C01 CMB well
图1. DFS-C01煤层气井历史排采曲线
期,由于储层所处地应力、后期改造等因素影响,压力仅在某方向传递或到达传递边界,煤层气产气量出现下降现象。
3. 水文参数计算
3.1. 导水系数计算
煤层气井在排采过程中,随着水位的下降引起储层压力的降低,在达到煤层气临界解吸压力以下煤层气开始解吸并通过孔裂隙运移至井筒 [10] 。煤层气井的排水降压过程实际上可以近似看作地下水承压完整井抽水试验。
根据泰斯公式,在抽水过程中产水量Q保持不变时,取两个时间段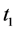 、
、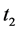 及相应的观测井(如果没有观测井,亦可粗略地将抽水井本身当作观测井 [11] )中的动液面下降值
及相应的观测井(如果没有观测井,亦可粗略地将抽水井本身当作观测井 [11] )中的动液面下降值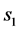 、
、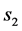 ,则有
,则有
 (1)
(1)
 (2)
(2)
上两式相除,得
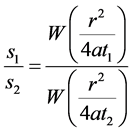 (3)
(3)
式(3)中只有压力传导系数 为未知数,由于它居于井函数之中,一般无法提出来,不能直接进行计算。采用试算法,根据经验给定一个
为未知数,由于它居于井函数之中,一般无法提出来,不能直接进行计算。采用试算法,根据经验给定一个 值,代入(3)式中看是否满足,如果不满足则另选取一个
值,代入(3)式中看是否满足,如果不满足则另选取一个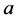 值直
值直
到满足为止。给定一个 值之后,
值之后, 则为已知数,即可根据
则为已知数,即可根据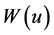 井函数表查出
井函数表查出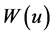 值,如果
值,如果
 之比值等于
之比值等于 时,则为满足。此时,
时,则为满足。此时, 值确定之后可按式(4)计算求导水系数T:
值确定之后可按式(4)计算求导水系数T: (4)
(4)
在试算过程中为减少误差,确保数值的准确,可多次计算求平均值来求出储层导水系数。
3.2. 影响半径计算(图2)
在煤层气排水采气过程中,地下水降落漏斗影响半径是一个至关重要的参数,它直接影响到煤层气解吸半径及储层压力梯度的计算。煤层气井排采过程的水力模型可近似看作非稳定流承压完整井抽水试验,故可采用定流量抽水时近似计算式(Jacob公式)来计算:
 (5)
(5)
式中:s,抽水影响范围内任意点任一时刻的水位降深(m);Q,煤层气井排采中的抽水量(m3/d);T,承压含水层导水系数(m2/d);t,自抽水至计算时刻的时间(d);r,计算点到煤层气井的距离(m); ,含水层储水系数。
,含水层储水系数。
根据煤层气井排采数据,通过试算法,在煤层气排采稳定时段内计算储水层导水系数,为减少误差,取多次计算平均值T,含水层储水系数按照经验给出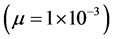 ,t分别按5,10,30,90,180,360,540,730 d给出,r分别按具体计算过程值给出进行试算,直到降深s = 0时达到降落漏斗边界(通过试算得到Re),同时将计算结果进行对数曲线拟合,回归得到对数方程。
,t分别按5,10,30,90,180,360,540,730 d给出,r分别按具体计算过程值给出进行试算,直到降深s = 0时达到降落漏斗边界(通过试算得到Re),同时将计算结果进行对数曲线拟合,回归得到对数方程。
3.3. 影响半经拟合结果
对研究区煤层气井进行阶段划分,然后在排采稳定时间段内利用式(4)及井函数表进行水文参数计算,得导水系数T =

Figure 2. Fitting curve of the influence radius for t days
图2. 抽水t天后的影响半径拟合曲线
表1. 不同时间段地下水头降深曲线的拟合方程
4. 储层水力模型建立
4.1. 模型建立假设
建立储层压力及产气量模型前先进行以下假设:
1) 煤储层所处区域最大主应力等于最小主应力;
2) 煤层为均质体;
3) 流体在储层孔–裂隙中的运动为层流,符合达西定律;
4) 忽略煤层气井在排采过程中的应力敏感效应、基质收缩效应和气体滑脱效应。
4.2. 储层压力参数模型建立
煤层气产出机理是当储层压力降低到解吸压力之下,煤储层中的煤层气得到由吸附态转为解吸,并在浓度差的作用下扩散至储层的孔–裂隙中,最后运移至井筒。根据Langmuir方程,可得临界解吸压力为:
 (6)
(6)
式中: 为实测含气量,m3/t;
为实测含气量,m3/t; 为兰氏压力,MPa;
为兰氏压力,MPa; 为兰氏体积,m3/t,
为兰氏体积,m3/t,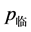 为临界解吸压力,MPa。通过煤层气含量实测和实验室吸附/解吸实验,得出
为临界解吸压力,MPa。通过煤层气含量实测和实验室吸附/解吸实验,得出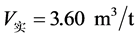 ,
,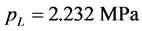 ,
, ,代入式(6)中得
,代入式(6)中得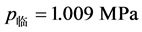 。
。
根据压力分布公式 [12] 得到井底压力 与解吸半径
与解吸半径 之间关系:
之间关系:
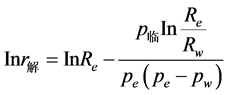 (7)
(7)
式中: 为储层压力,MPa;
为储层压力,MPa; 为井底压力,MPa;
为井底压力,MPa;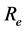 为影响半径,m;
为影响半径,m;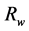 为井半径,m;
为井半径,m; 为压力传递至解吸压力时至井筒距离,m。结合Langmuir方程和压力分布公式得到含气量与影响半径之间
为压力传递至解吸压力时至井筒距离,m。结合Langmuir方程和压力分布公式得到含气量与影响半径之间 关系:
关系:
 (8)
(8)
以煤层顶板水平面为横坐标,井筒中心为纵坐标,建立坐标系(图3),得到解吸半径下的解吸高度H:
 (9)
(9)
式中:M为煤层厚度,m;H为在解吸半径r下的解吸高度,m。
在解吸体积内取一微小环形,通过微积分得到解吸半径分为内的产气量模型为:
 (10)
(10)
井底压力是指煤层气井井底的流体流动压力,包括三部分:井口套压、油管和套管之间的环空纯气压力和混气液柱压力井底压力的计算,在实际生产中主要通过产水量改变液柱压力来调节井底压力。在缺乏原始资料情况下可根据邻近井排采数据,建立不同阶段井底压力与产水量之间的关系,如表2所示,亦可在排采前期认为控制井底压力。
由表1拟合出影响半径 和时间t之间关系:
和时间t之间关系:

Figure 3. Cone of depression and model of pressure transfer in drainage process
图3. 排采过程降落漏斗与压力传递模型
表2. 不同阶段井底压力与产水量关系
 (11)
(11)
其中, ,
, ,结合式(7)、式(8)、式(9)和式(10),计算出井底压力、日产气量随时间的变化并绘制模拟曲线。
,结合式(7)、式(8)、式(9)和式(10),计算出井底压力、日产气量随时间的变化并绘制模拟曲线。
4.3. 模拟结果
利用数学软件进行编程,计算出产气结果,对计算结果进行曲线绘制(图4)。
将模拟结果和大佛寺井田DFS-C01井实际排采曲线进行对比,曲线变化情况较为吻合,实际排采井的井底压力随着排采的进行逐渐减小,而产气曲线表现出“驼峰式”变化,模拟的结果显示产气量在
从计算结果看,煤储层的渗透性对煤层气井整个排采的过程影响很大,它直接影响到降落漏斗影响半径的大小,从而影响煤层气解吸半径和解吸率,最终反映在产气量上。所以要提高煤层气井产气量,提高煤储层的渗透系数,扩大影响半径是关键手段。
5. 结论
1) 本文研究了在地质资料不足的情况下,根据低阶煤地区的煤层气单井的排采数据及试井资料来建立煤层气井排采初期的地下水动力模型。
2) 煤层气井排采过程中,在不同阶段井底压力与产水量呈现线性变化。在排采后期,井底流压基本保持不变,而影响半径稳定而缓慢扩展,最终到达扩展边界。
3) 根据拟合结果发现,煤层气排采过程中影响半径随时间呈现幂函数关系,随液面降深呈对数关系。
4) 从煤层开采时与压裂储层时注入水量计算,煤层气井排采水极有可能含有煤层顶板上方的承压水,在进行储层改善时压穿顶底板,将煤层与顶板沟通。排采过程中通过抽取煤层顶板上方承压含水层的水,形成降落漏斗,而在煤储层中形成相似的储层压力梯度曲线,使得解吸半径内的煤层气得到不同程度的解吸并通过孔–裂隙运移至井筒。
5) 煤层气排采过程中,在客观因素上产气量的关键在于降落漏斗影响半径和煤储层的渗透系数,这对煤层气排采的主要动力影响巨大。

Figure 4. Simulated production curves of the DFS-C01 CBM well
图4. DFS-C01煤层气井模拟排采曲线
基金项目
山西省煤层气联合研究基金项目(2013012009),国家科技重大专项(2011ZX05061-005-002)。
参考文献 (References)
[1] 孟召平, 王保玉, 谢晓彤, 等 (2012) 煤岩变形力学特性及其对渗透性的控制. 煤炭学报, 8, 1342-1347.
[2] 傅雪海, 秦勇, 韦重韬 (2007) 煤层气地质学. 中国矿业大学出版社, 徐州, 117-124.
[3] 汪吉林, 秦勇, 傅雪海 (2012) 关于煤层气排采动态变化机制的新认识. 高校地质学报, 3, 583-588.
[4] 陶树 (2011) 沁南煤储层渗透率动态变化效应及气井产能响应. 中国地质大学, 北京, 2-6.
[5] 杨秀春, 季明宅 (2008) 煤层气排采动态参数及其相互关系. 煤田地质与勘探, 2, 19-27.
[6] 秦勇, 汤达祯, 刘大锰, 等 (2014) 煤储层开发动态地质评价理论与技术进展. 煤炭科学技术, 1, 80-88.
[7] 罗振兴, 李铁军, 郭大立, 等 (2012) 煤层气排采曲线类型划分及排采因素分析. 重庆科技学院学报(自然科学版), 4, 56-59.
[8] 倪小明, 苏现波, 张小东 (2010) 煤层气开发地质学. 化学工业出版社, 北京, 165-166.
[9] 姚帅, 吴财芳, 李腾 (2014) 潘庄区块煤层气井层间干扰数值模拟研究. 煤炭工程, 3, 80-83.
[10] 罗克勇 (2011) 煤层气水平井排采控制研究. 西安科技大学, 西安, 20-21.
[11] 刘兆昌, 朱琨 (2010) 供水水文地学. 中国建筑工业出版社, 北京, 80-81.
[12] 倪小明, 王延斌, 接铭训, 等 (2007) 煤层气井排采初期合理排采强度的确定方法. 西南石油大学学报, 6, 101- 104.
