Journal of Electrical Engineering
Vol.2 No.02(2014), Article
ID:13466,8
pages
DOI:10.12677/JEE.2014.22002
Detection and Localization of Power Quality Disturbances Based on Complex Wavelet
1College of Electrical and Information Engineering, Hunan University, Changsha
2Jiangxi Electric Power Research Institute, Nanchang
3Hunan HDHL Electrical & Information Technology Co., Ltd., Changsha
Email: wuzhaogang163@163.com, yaojiangang@126.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Mar. 26th, 2014; revised: Apr. 1st, 2014; accepted: Apr. 8th, 2014
ABSTRACT
Detection and localization of power quality disturbance signals provide a basis to analyze the causes of the disturbance. This paper presents a complex wavelet-based power quality disturbance detection and localization. First of all, the amplitude and phase of complex wavelet coefficients are extracted by discrete complex wavelet transform, and then, the composite information of amplitude and phase is used to achieving fast and accurate positioning of 5 kinds of transient power quality disturbance signals. Under the condition of noise and disturbance characteristics is not obvious, this paper proposes an auxiliary positioning method based on signal preprocessing. Simulation shows, under the condition of noise, the method can achieve fast and exact positioning of power quality disturbance signals.
Keywords:Power Quality, Disturbances Location, Complex Wavelet Transform, Assisted Positioning

基于复小波的电能质量扰动检测与定位
吴兆刚1,姚建刚1,李唐兵2,陈 强1,杨 政1,龚文龙3
1湖南大学,电气与信息工程学院,长沙
2江西省电力科学研究院,南昌
3湖南湖大华龙电气与信息技术有限公司,长沙
Email: wuzhaogang163@163.com, yaojiangang@126.com
收稿日期:2014年3月26日;修回日期:2014年4月1日;录用日期:2014年4月8日

摘 要
电能质量扰动信号的检测与定位为分析扰动产生的原因提供依据。本文提出了一种基于复小波的电能质量扰动检测与定位方法,该方法利用离散复小波变换,提取扰动信号的复小波系数的幅值和相位信息,再利用幅值和相位的复合信息实现对5种暂态电能质量扰动信号的快速准确定位。针对噪声条件下的扰动特征不明显时的定位,提出了一种基于信号预处理的辅助定位方法。仿真表明,该方法能在噪声条件下实现对电能质量扰动信号的快速准确定位。
关键词
电能质量,扰动定位,复小波变换,辅助定位

1. 引言
近年来,电能质量问题已被电力部门以及电力用户广泛关注,对电能质量扰动信号进行及时、准确地检测与定位,是监测和治理电能质量的前提和依据,因而对扰动的检测与定位的研究有着重要意义。电能质量扰动的检测与定位实质是对扰动信号的奇异点检测,但扰动信号奇异点的检测与定位容易受到噪声的影响,在噪声条件下检测出扰动信号的突变点是准确定位扰动起止时间的关键。
小波变换是扰动检测与定位应用中最常见的方法,其中最为经典的是小波变换模极大值原理对扰动信号的突变点的检测。与实小波变换相比,复小波相频特性不仅可改变小波变换域的能量集中程度,还可改变小波提取信号中具有不同特点的信息的能力,因此为取得最佳小波分析效果,需要从小波信号的幅频、相频特性去分析[1] 。
本文利用db实小波构造出相应的复小波,对加入噪声的扰动信号作离散复小波变换,利用一种幅值、相位复合信息检测暂态扰动信号的的起止时间点。针对噪声背景下信号过零点附近发生扰动时检测不出来的情况,提出了相应的辅助定位方法,实现了在噪声条件下对信号过零点附近发生扰动的时间定位。
2. 小波变换和多分辨分析
小波(wavelet)变换是由法国物理学家Grossmann与法国数学家Morlet等共同提出的,是当代应用数学中一个迅速发展起来的领域。与傅立叶变换、窗口傅立叶变换相比,小波是时间和频率的局部变换,其本质是度量被分析信号波形与所用小波波形的局部相似程度。
2.1. 连续小波变换
假设![]() ,并且满足约束条件
,并且满足约束条件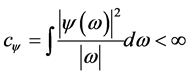 和
和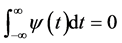 的母小波时,对于任意函数
的母小波时,对于任意函数![]() 的连续小波变换式:
的连续小波变换式:
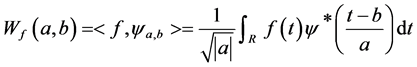 (1)
(1)
上式中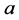 为伸缩参数,b为平移参数。
为伸缩参数,b为平移参数。
2.2. 离散小波变换
式(1)中参数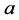 、b取连续值时是连续小波变换,主要应用在于理论研究。在实际应用中,
、b取连续值时是连续小波变换,主要应用在于理论研究。在实际应用中,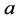 、b作离散化处理,离散小波变换为:
、b作离散化处理,离散小波变换为:
 (2)
(2)
式中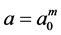 ,
,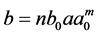 ,m、n是整数,
,m、n是整数,![]() 是大于1的伸缩步长,
是大于1的伸缩步长,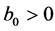 且与母小波形式有关。
且与母小波形式有关。
3. 复小波变换以及在扰动信号定位原理
3.1. 复小波变化
在实小波变换中只能得到信号的幅值信息,而实际中信号的相位信息也包含了信号的很多信息,因此用复小波变换获得信号的相位信息是非常有必要的。在小波变换式(1)和(2)中,当选用的小波基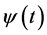 为复数形式时,称其为复小波变换。
为复数形式时,称其为复小波变换。
MATLAB工具箱的复小波只能实现连续变换,很难应用于实际,因此需要构造出能实现离散变换的正交复小波。小波理论和滤波器组(Filter Banks)之间关系的揭示,使得滤波器理论对小波变换进行小波函数的构造以及小波变换应用范围等方面开辟了一条新的途径,也为以滤波器理论为基础的各种新型小波的出现提供了可能和理论基础[2] 。小波实际上就是一种具有特定性质的带通滤波器,而离散正交小波基对应的就是满足一定条件的完全重构滤波器[3] 。因此可通过设计滤波器来构造相应的小波,实数滤波器系数对应实小波,复数波系数对应复小波。
3.2. 复小波定位原理与复小波的选取
函数在某处有间断点或某阶导数不连续时,则称这个函数在此处具有奇异性,称该点为函数的奇异点。信号的奇异点检测可用实小波变换的模极大值原理获取,同样复小波变换的幅值和相位信息可以同时检测到信号的奇异点。若选用复值小波对故障信号进行分析,在小波变换幅值不太明显的情况下,可借助于相位信息敏感地捕捉故障信号奇异点[4] 。因而,利用复小波的幅值与相位复合信息能实现快速准确的定位。
选用适合的复小波可以实现在尺度1上的准确定位。文献[5] 指出不具有消失矩的小波是不能检测高阶奇异点的,低阶消失矩小波不易检测高阶奇异点,高阶消失矩小波能很容易探测出高阶奇异点和低阶奇异点。因此,在检测扰动信号时,应选用具有一定消失矩的小波;当然,过高的消失矩也不合适,这会增加计算量而且低阶奇异点会变模糊。在非平稳信号处理时,选用的小波基还需要考虑紧支性。Daubechies系列小波具有正交、时频紧支撑和Mallat快速算法等优点,在检测暂态电能质量扰动信号时有很好的效果。文献[6] 指出:在db小波系列中,db4小波具有最短的时间窗和最高的时间分辨率,在非平稳信号的时间定位中可获得最佳的效果。暂态电能质量扰动信号属于非平稳信号,因此在实小波分析中常选用db4小波进行检测与定位分析。因而,这里根据文献[7] 中的复小波构造方法,以db4实小波为基础构造其复小波,复小波滤波器组系数如表1。
4. 离散复小波定位方法
4.1. 扰动信号的生成和参数设置
用MATLAB仿真生成暂态电能质量扰动的波形,扰动的数学模型参照文献[8] 中的暂态电能质量扰动模型,包括3种短时扰动(电压暂升、电压暂降、电压中断)和2种暂态扰动(暂态脉冲、暂态震荡)共5种扰动。为模拟实际情况,扰动的参数(如扰动起止时间、扰动幅值)在允许范围内随机变化。模型数据窗设置为0.2秒,即10个周波的长度,采样频率设置为6400 Hz,在扰动模型中加入40 db的白噪声。
4.2. 辅助定位方法
复小波可以快速准确的定位,在噪声干扰条件下,如果电压暂升、电压暂降和电压中断扰动发生在幅值过零点附近时,直接用复小波变换将检测不出来。在这种情况下,将要用到辅助定位方法。
在噪声背景下检测短时电能质量扰动起止时间时,先直接用复小波变换定位,如果出现两个点(或者一个点)检测不出来的情况,这时可以判断扰动点属于过零点类型,将用到辅助定位方法。具体方法是先用实小波(db4)对扰动信号做4层分解,重构第4层低频段信号sign1,在同样噪声背景下生成正常信号sign2,对sign1和sign2分别进行复小波变换后得到复小波系数d1和d2,取复系数d = d1 − d2,辅助定位的复合信息用复数d的实部与虚部的乘积,其流程如图1。
表1. db4复小波滤波器系数
其中,h、g对应的是分解滤波器系数,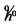 、
、![]() 对应的是重构滤波器系数。
对应的是重构滤波器系数。
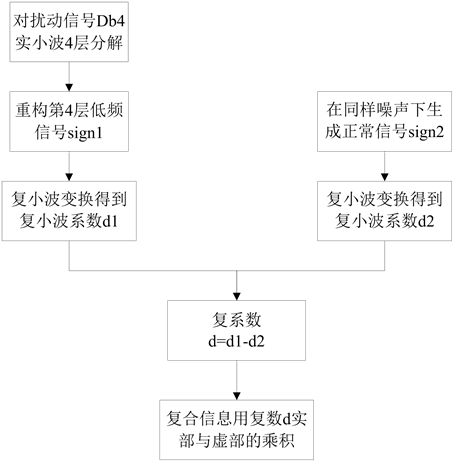
Figure 1. A flowchart of assisted positioning methods
图1. 辅助定位方法流程图
5. 仿真分析
如图2~6所示,在无噪声条件下的电压暂升、电压暂降、电压中断、暂态脉冲和暂态震荡的db4复小波变换定位仿真图。图中子图(1)是扰动信号波形,子图(2)是复小波变换的复小波系数幅值图,子图(3)是复小波系数相位图,子图(4)是复小波系数复合信息图,复合信息取幅值与相位的乘积。图2~6可以直观地看到,一个尺度的复小波变换信息就可以定位信号扰动,且定位时间可以直接从图中的模极大值坐标获取。
如表2是以上5五种暂态电能质量扰动的实际扰动起止时间与复小波定位实测起止时间,比较数据可知,复小波定位误差非常小,在0.0005秒之内,且有较为明显的的特征,那就是定位的时间都是向后延时的,延时时间在0.0002~0.0005秒之间,这样可以把定位的时间减去一个延时时间(比如0.00035毫秒)
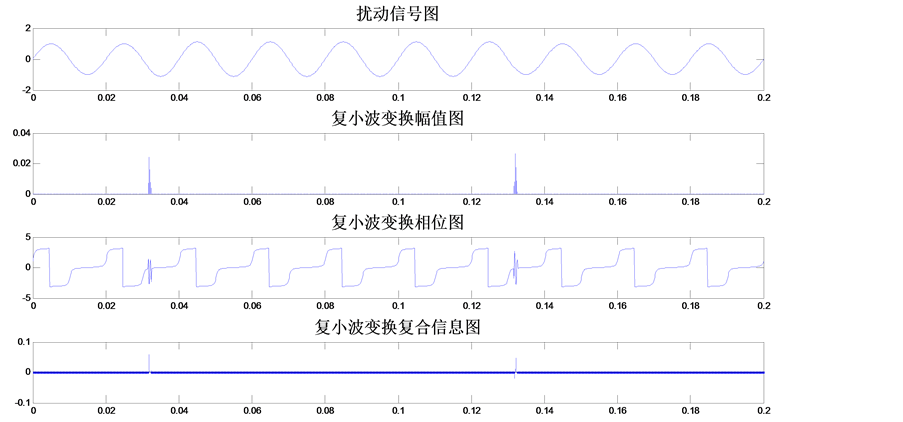
Figure 2. Voltage swell CWT
图2. 电压暂升复小波变换
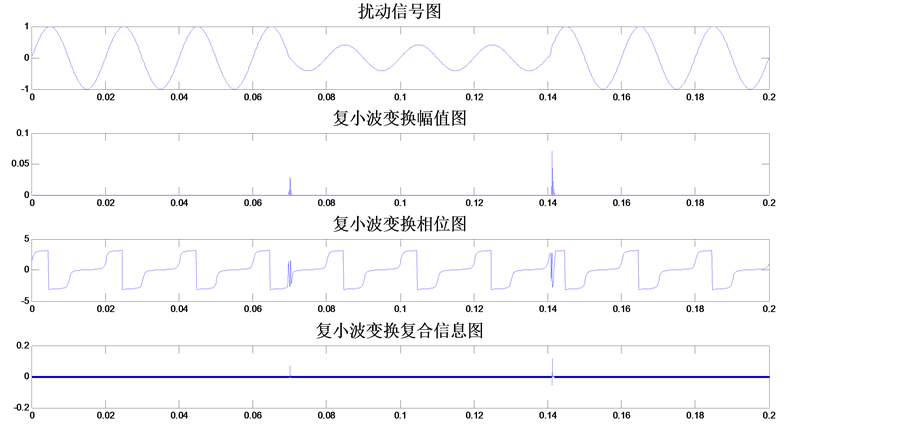
Figure 3. Voltage sags CWT
图3. 电压暂降复小波变换

Figure 4. Voltage interruption CWT
图4. 电压中断复小波变换

Figure 5. Transient impulse CWT
图5. 暂态脉冲复小波变换
表2. 扰动实际时间与复小波定位时间对比
来校正实测起止时间,这时的误差可以控制在0.0002秒左右。
如图7是在信号中加入信噪比为40 db的白噪声后的电压暂升信号复小波变换,开始时间设定为t1 = 0.04 s,结束时间设定为t2 = 0.08 s。大量仿真发现,短时电能质量扰动信号(如电压暂升、电压暂降和电压中断)起止时间发生在幅值过零点附近时,对信号直接使用复小波变换时将出现如图7那样不能定位的情况。
复小波可以快速准确的定位扰动信号起止时间,但在噪声干扰条件下,当电压暂升、电压暂降和电压中断扰动起止时间发生在幅值过零点附近时,直接对信号用复小波变换将检测不出来。在这种情况下,可以使用辅助定位方法,对扰动信号作出预处理,采取的方法是小波分解与重构,提取低频段重构信号,用复小波检测重构信号,能够判断出扰动点起止时间。

Figure 6. Transient oscillation CWT
图6. 暂态震荡复小波变换
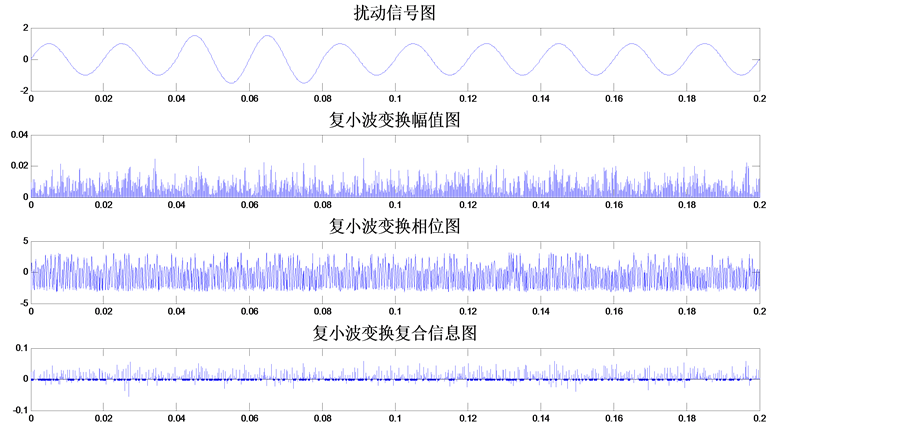
Figure 7. Voltage swell CWT under noisy conditions
图7. 含噪声电压暂升复小波变换
设定电压暂升的开始时间t1 = 0.04 s,结束时间t2 = 0.08 s,信号中添加40 db白噪声。仿真如图8的辅助定位方法,上面为子图(1),下面为子图(2)。其中子图(1)是直接复小波变换后的复合信息,在这种情况下子图(1)是不能定位的;子图(2)是辅助定位方法,结合上文提到的延时现象,从子图(2)中可以判断是0.04 s和0.08 s过零点附近发生了扰动。这种判断过零点扰动的定位方法是有误差的,根据仿真现象可以判定这种误差在0.0008 s以内,因为在过零点0.0008 s之外的扰动起止点,直接复小波变换是可以定位出来的。
如图9是起止时间为t1 = 0.04 s,t2 = 0.0808 s的电压暂升定位仿真(噪声条件40 db白噪声)的综合定位方法,用到直接定位和辅助定位两种方法实现最终的定位。子图(1)是直接复小波变换,如图可以判断一个点是0.0812 s,再通过辅助定位的子图(2)可以大致判断两个点0.04 s和0.08 s。优先选取直接复小波
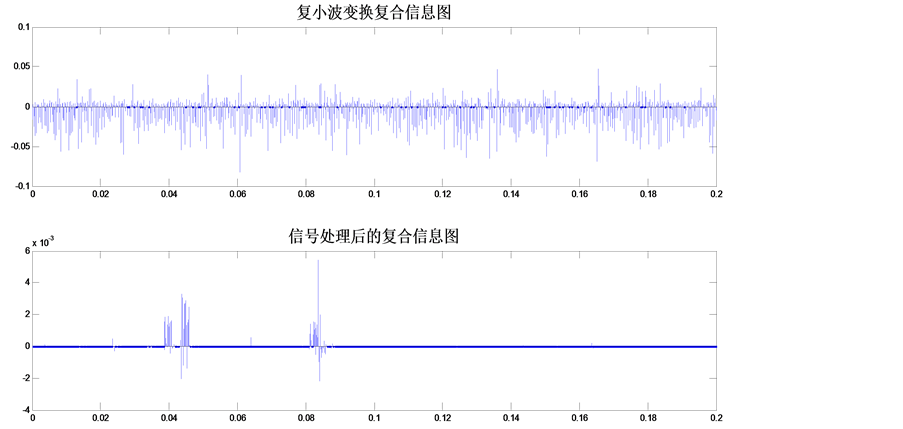
Figure 8. Positioning voltage swell in assisted methods
图8. 辅助方法电压暂升定位
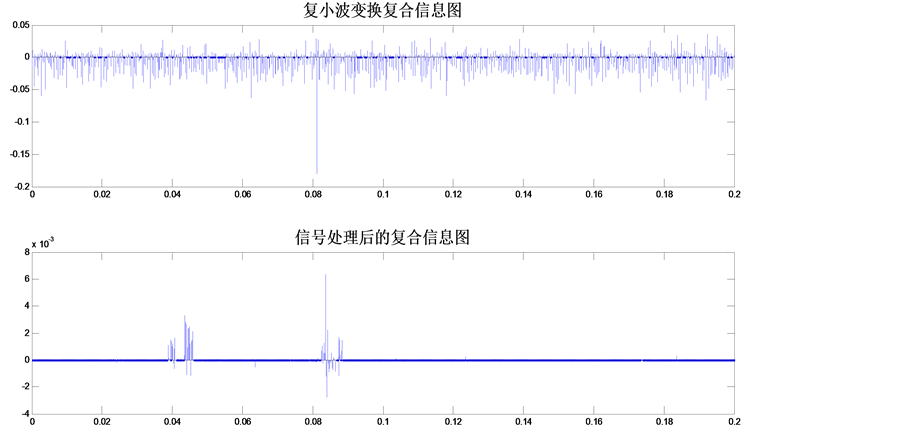
Figure 9. Positioning voltage swell in mixture methods
图9. 综合方法电压暂升定位
变换定位的点(0.0812 s),结合辅助定位信息,可以完成定位,其定位起止点为0.04 s和0.0812 s。引入校正延时量(0.00035 s),最终的定位起止点可以校正为0.04 s和0.08085 s,这与真实值非常接近了。电压暂降和电压中断可以用同样的方法定位,这里不再详细介绍。
6. 结论
复小波变换非常适合暂态电能质量信号的定位,尤其是生成的db4复小波,其变换的幅值和相位的复合信息能实现扰动的快速准确的定位。针对在噪声环境下定位时出现的信号幅值过零点附近的扰动点无法定位的情况,提出了一种辅助定位方法,仿真证明该方法有较好的定位效果,能实现噪声条件下的快速准确定位。
参考文献 (References)
- [1] 唐炬, 谢颜斌, 朱伟等 (2006) 用于提取GIS局部放电信号的正交紧支复小波构造研究. 电工技术学报, 21, 87- 91.
- [2] 耿云玲, 王群, 何怡刚 (2006) 基于复数小波相位信息的电能质量扰动的检测, 定位与分类. 电工技术学报, 21, 112-116.
- [3] Vetterli, M. and Herley, C. (1992) Wavelets and filter banks: Theory and design. IEEE Transactions on SP, 40, 2207- 2232.
- [4] 何建军, 周宏 (1999) 电力系统奇异信号的复值小波分析. 中国电机工程学报, 19, 1-4.
- [5] 何正友, 钱清泉 (2003) 电力系统暂态信号分析中小波基的选择原则. 电力系统自动化, 27, 45-48.
- [6] Brito, N.S.D., Souza, B.A. and Pires, F.A.C. (1998) Daubechies wavelets in quality of electrical power. Proceeding of IEEE ICHQP, Athens, 511-515.
- [7] 刘守亮, 肖先勇 (2005) Daubechies复小波的生成及其在短时电能质量扰动检测中的应用. 电工技术学报, 20, 106-110.
- [8] 张全明, 刘会金 (2008) 最小二乘支持向量机在电能质量扰动分类中的应用. 中国电机工程学报, 28, 106-110.
