Journal of Electrical Engineering
Vol.
06
No.
04
(
2018
), Article ID:
27564
,
8
pages
10.12677/JEE.2018.64033
Design of Two-Dimensional Ultrasonic Wind Speed Measurement System Based on STM32F103ZET6
Weidong Wang
School of Electrical Engineering and Automation, Tianjin Polytechnic University, Tianjin
Received: Oct. 26th, 2018; accepted: Nov. 8th, 2018; published: Nov. 15th, 2018

ABSTRACT
The accuracy of wind speed measurement is important for the observation of the ocean-atmosphere interface. This paper briefly describes the advantages of the time difference ultrasonic wind speed measurement method, and based on the two-dimensional V-structure ultrasonic measurement principle of time difference method, a two-dimensional ultrasonic wind speed measurement system based on STM32F103ZET6 is built. Compared with traditional wind measurement systems, the design introduces the Hilbert Huang Transform algorithm to process the measurement data, which can ensure the accuracy of the wind speed measurement. The experimental results show that the design has strong adaptability and can achieve high precision wind speed measurement. It has high reference value and practical significance in the observation of complex meteorological environment such as air-sea interface.
Keywords:Air Sea Interface, Ultrasonic Wave, Time Difference Method, STM32F103ZET6, Hilbert Huang Transform
基于STM32F103ZET6的二维超声波风速测量系统设计
王威栋
天津工业大学电气工程与自动化学院,天津
收稿日期:2018年10月26日;录用日期:2018年11月8日;发布日期:2018年11月15日

摘 要
风速测量的准确性对于海洋-大气界面的观测有着重要意义。本文简述了时间差超声波风速测量方法的优点,并运用时间差法的二维V型结构超声波测量原理,搭建了一种基于STM32F103ZET6的二维超声波风速测量系统。与传统的测风系统相比较,该设计引入希尔伯特黄变换对测量数据进行处理,能够保证风速测量的准确性。实验结果表明:该设计适应性较强,可实现较高精度的风速测量,在海气界面等复杂气象环境的观测中具有较高的参考价值和实用意义。
关键词 :海气界面,超声波,时差法,STM32F103ZET6,希尔伯特黄变换

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
目前,传统的风速测量仪大多是利用机械构件的转动来衡量风速 [1] 。与超声波风速仪相比,存在几点缺陷:1) 旋转部件会产生摩擦损耗;2) 存在启动风速,需要启动时间;3) 在海气界面中机械旋转构件的抗浸蚀性能较差 [2] 。
超声波风速仪与HHT算法相结合,不仅弥补了以上缺陷,而且在风速测量精度上有所提高、抗恶劣海况能力增强,成为当下的研究热点。本文简单介绍了一种基于微控制器STM32F103ZET6、运用时间差法设计的二维超声波测风仪,并引入HHT算法对测量数据进行处理。该系统测量精度高、体积小、频率快、稳定性强,十分适用于海洋大气界面等海洋环境的风速测量。
2. 时间差测风方法
目前时间差法最为成熟,运用也最为广泛,同样也适用于在海洋环境下的风速测量。当波程一定时,分别在顺、逆风的情况下,超声波的输送有一个速率差,而这个速率差就对应一个时间差,两者之间是线性关系 [3] 。
本方法为:4个收发同体的超声波换能器分别放置在东西南北四个方位,两两间隔分别相等 [4] 。如图1所示,本设计采用V型安装位置,这样在缩小仪器体积的同时,固定了超声波的传播方向、扩大了超声波声程。

Figure 1. V-type measurement schematic
图1. V型测量原理图
当静风时,设超声波波速为c,真实风速为v [5] 。当有风时,顺、逆风向的时长 , 和一维风速v的关系为:
(1)
(2)
(3)
在二维情况下,在一个平面的X和Y方位上垂向放置两对换能器 [6] 。 和 依次对应实际风速在X、Y方向上的分解(如图2所示)。
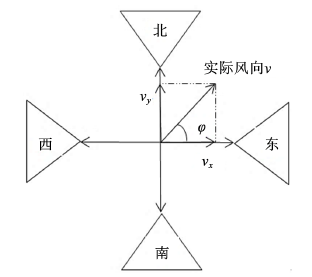
Figure 2. Wind speed vector
图2. 风速矢量图
假设顺风向时东西方向上的输送时长是 、逆风向时为 ,那么同样 和 分别为南北方向上输送的的顺、逆风时长 [6] 。
(4)
(5)
实际风速为:
(6)
时间差法的原理较为简单,在测量中不易受环境等因素的影响。不仅电路容易实现、具有稳定的性能,而且方便提高电路集成度,降低板上设计面积。
3. 系统方案设计
3.1. 整体方案设计
本方案以STM32F103ZET6为核心,通过产生时序信号来激励发生端工作 [7] 。如图3所示,整个系统由电源模块、超声波发射驱动模块、超声波接收模块、滤波放大模块、UART通信模块和A/D采样模块等组成 [8] 。

Figure 3. System overall composition
图3. 系统总体构成图
3.2. 硬件设计
3.2.1. 超声波发射驱动模块
本设计用激励信号PWM波配合LC滤波来共同实现DAC输出 [9] (如图4所示)。

Figure 4. Typical PWM waveform of the actual circuit
图4. 实际电路的典型PWM波形
3.2.2. 超声波接收模块
LC选频电路如图5所示:左侧是一个74HC238D译码器,而右侧是发射、接收电路。1、2和3分别是由STM32F103ZET6控制的地址输入;K1、K2、K3和K4作为输出端。S1、S3与收、发兼具的声波探头相连接,CH1和CH3为收到的信号 [10] 。E1、E2、E3是译码器的势能点,连接控制器I/O口PB3与PB4。由S3侧的探头接收,测得CH3的回波信号数据并保存 [11] 。
3.2.3. 信号采集保存
本设计采用TI公司的ADS1298芯片用于多路信号的同时取样,整合了8通道同时采样的24位Delta-Sigma ADC、增益放大器(PGA)、reference voltage和oscillator [9] ,数据速率250 SPS到32 kSPS。特点是性能优越、取样精确。
3.3. HHT算法简介
为了更好地应对非线性或非平稳性数据的处理数据方法,Huang等人在1998年首次提出将希尔伯特变换(HT)和经验模态分解(EMD)相结合的方法,NASA称之为希尔伯特–黄变换(HHT)。该方法不需要对基函数预先设定,首先,通过经验模态分解,将任何繁复的信号分解成有限个IMF分量和一个剩余分量,能够反映各个时间尺度的变化;其次,对IMF分量运用希尔伯特变换,从而得出每个模态的瞬时频率。该频率能反映数据随时间的变化特性。

Figure 5. Ultrasonic receiver module
图5. 超声波接收模块
如图6所示,EMD基本步骤如下:
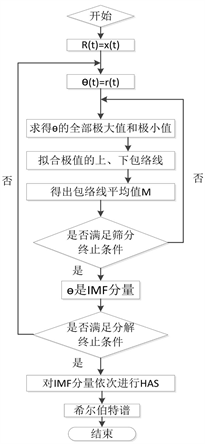
Figure 6. HHT flow chart
图6. HHT流程图
1) 基于原始信号 ,通过三次样条插值法处理极大值和极小值点,得到上、下包络线的平均值为:
(7)
2) 计算原始信号 与平均值 的差值:
(8)
3) 如果满足IMF条件,那么分解停止;如果不满足IMF条件,那么将上述步骤重复直到满足条件,令剩余分量为 :
 (9)
(9)
4) 用剩余分量作为新的信号反复以上的步骤,分离出来所有的IMF分量与剩余分量的关系如下:
(10)
4. 实验结果与分析
按照海滨观测规范中规定的观测和记录方法,分别在顺风向和逆风向的条件下,每3秒采集一次,记录到0.1 m/s,从4个不同测量点上分别选取一定的数据进行对比。如图7所示。

Figure 7. System test physical chart
图7. 系统测试实物图
由实验数据分析可知,实验区域为0~3 m/s,每隔0.1 m/s选取一个点进行试验,总共30个测量点,各测量点符合在0~5 m/s的范围内,风速测量准确度在 ± 0.5 m/s的测量精度要求。将所得数据导入上位机进行滤波,图8为顺风向超声波接收信号波形图,图9为逆风向超声波接收信号波形图。
4.1. 实验结论
1) 在低风速情况下,采用时差法超声波测风原理能够分别测量出超声波换能器接收到的顺风和逆风时的超声波回波信号,从而测量出风速值;
2) 基于一定数量的试验,运用HHT算法进行数据处理,验证了本文设计的具有较高精确度和稳定性。已知空气中的波速340 m/s,本设计里两对换能器之间传输声程均是140 mm,可得传播时间间隔为0.41 ms [10] ;相比较而言,STM32F的最高时钟为72 MHz,可知时间精确度最高可达14 ns。
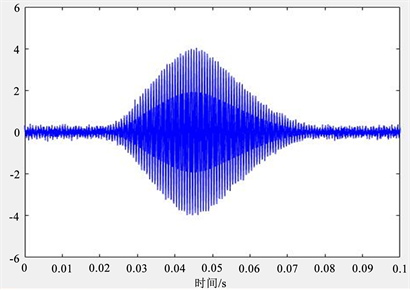
Figure 8. Downwind wave receiving signal waveform
图8. 顺风向超声波接收信号波形图
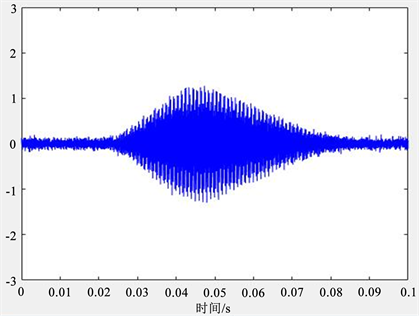
Figure 9. Upwind direction ultrasonic receiving signal waveform
图9. 逆风向超声波接收信号波形图
4.2. 误差的原因分析
1) 受电路板面积的影响,实时的温度补偿电路并没有添加,而是将测得的外部环境温度写入程序中,从而将测量误差引入系统 [12] ;
2) 用时间差法测量出的低风速值精度基本满足要求。但是在中、高风速情况下,还需要进一步的验证测试 [13] 。
5. 结束语
在海气界面的复杂天气中,由于传统仪器存在偏差大、保障难度大等问题,本文对超声波测风系统的原理和硬件设计进行了较为详细的介绍,整体设计电路简单,易于调试。本设计虽然实现了测量风速的基本功能,但在某些方面也需要改进:
1) 外界温湿度也会影响风速,可以添加温湿度补偿器来增强测风仪的性能;
2) 在数据处理方面引入新的算法来提高准确性。
文章引用
王威栋. 基于STM32F103ZET6的二维超声波风速测量系统设计
Design of Two-Dimensional Ultrasonic Wind Speed Measurement System Based on STM32F103ZET6[J]. 电气工程, 2018, 06(04): 283-290. https://doi.org/10.12677/JEE.2018.64033
参考文献
- 1. 陈志洲, 刘小河, 田雨聪. 基于 STM32 单片机测风系统的设计[J]. 电气技术, 2016(5): 31-35+44.
- 2. 刘德荣, 王瑛, 王铁流, 张炳洋. 基于STM32F的超声波风速风向仪设计[J]. 测控技术, 2017, 36(6): 97-100.
- 3. 温玉波.海洋环境基础数据格式转换的研究[D]: [硕士学位论文]. 青岛: 中国海洋大学, 2014.
- 4. 李聪, 国红玉, 王峰. 二维超声波风速仪[J]. 仪表技术与传感, 2015(2): 29-32.
- 5. 梁家怡, 超声波二维风速风向测量系统设计[D]: [硕士学位论文]. 哈尔滨: 哈尔滨理工大学, 2013.
- 6. 崔国恒, 赵金超, 曹可劲, 等. 基于凹面反射的超声风速测量系统设计与实现[J]. 声学技术, 2014, 33(4): 336-340.
- 7. 行鸿彦, 于祥, 邹水平, 等. 风杯式风速传感器启动风速校准实验箱的分析与设计[J]. 仪器仪表学报, 2015, 36(9): 1996-2004.
- 8. 高中华, 赵湛, 杜利东, 等. 超声波风速风向仪的电路设计[J]. 仪表技术与传感器, 2014(1): 19-20.
- 9. 杨帆. 嵌入式系统在智能便携式自动气象站中的研究与应用[D]: [硕士学位论文]. 南京: 南京航空航天大学, 2012.
- 10. 全鹏程, 易仕和, 武宇, 等. 激波与层流/湍流边界层相互作用实验研究[J]. 物理学报, 2014, 63(8): 239-243.
- 11. Kim, M. (2015) Test Bench Development for Acquisition Module FPGA of Ultrasonic Flow Meter. 2015 International Conference on Pervasive Computing, 1-6.
- 12. Bucci, G., Ciancetta, F., Fiorucci, E., et al. (2013) A Low-Cost Ultrasonic Wind Speed and Direction Measurement System. 2013 IEEE International Instrumentation and Measurement Technology Conference, 505-510.
- 13. 陈子建, 王振涛, 许杰斌. EMD 技术在船舶液压设备故障诊断中的应用研究[J]. 机械工程与技术, 2017, 6(4): 324-335.