Modern Management
Vol.07 No.05(2017), Article ID:21959,9
pages
10.12677/MM.2017.75026
Financial Risk Early Warning Model of Decision Tree Research Based on Z-Score Indicators
Yunyi Yang, Zhonghe Sun, Jing Lu
IT Center, China National Audit Office, Beijing
Received: Aug. 16th, 2017; accepted: Aug. 31st, 2017; published: Sep. 7th, 2017

ABSTRACT
Financial risk early warning model is one of the primary means of forecasting financial crisis. Z-score model has been applied widely since it has precise formula and good practicability. However, as regard to the adequacy of using Z-score model to forecast financial crisis for domestic companies, there is a dispute. Therefore, we collect financial statements data from 2007-2013 of Shanghai listed companies, and prove that Z scores between ST companies and non-ST companies are linearly inseparable. It reveals that Z-score model with linear separable principle in nature, has its own limitation. Hence, this paper brings up a financial risk early warning model of decision tree based on Z-score indicators and it solves the problem of Z-score model. The empirical research shows that the decision model given by this paper can forecast financial crisis three years before it happens with 75.37% accuracy, and with 95.45% accuracy one year ahead of crisis occurance.
Keywords:Financial Risk Early Warning, Z-Score, Decision Tree
基于Z-Score指标决策树的财务风险预警 模型研究
杨蕴毅,孙中和,卢靖
审计署计算机技术中心,北京
收稿日期:2017年8月16日;录用日期:2017年8月31日;发布日期:2017年9月7日

摘 要
财务风险预警模型是预测财务危机的主要手段之一。Z分数模型以其公式严谨、可操作性强等特点,被广泛应用。然而,Z分数模型是否适用于预警中国企业的财务危机仍存在争议。为此,归集了沪市上市公司2007~2013年的财务报表数据,实证发现ST公司与非ST公司的Z值线性不可分。揭示了:本质上为线性区分方法的Z分数模型存在局限性。因此,利用Z分数模型原有指标,提出了基于决策树的财务风险预警模型,解决Z分数模型失效问题。实证研究表明:所提出的预警模型提前3年预测ST公司财务危机的准确率达75.37%,提前1年预测的准确率达95.45%。
关键词 :财务风险预警,Z-score,决策树

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
国内学者胡剑(2014)提出财务风险是在公司各项财务活动中,由于内外部环境及难以预料或无法控制的因素使财务系统运行偏离预期目标而形成的经济损失的机会性或可能性 [1] 。财务风险客观存在,虽不能完全消除,但可预防和降低。
财务风险预警的主要手段之一是建立财务风险预警模型。一个好的财务风险预警模型不仅能给投资者及早带来预警信号,及时做出决策规避风险,还能帮助企业管理层提早发现企业财务恶化的征兆,预防财务危机。财务风险预警模型有单变量和多变量两种模式。早在20世纪三十年代,西方经济学学家帕特里克就运用单个财务比率对公司财务风险进行预警研究。在多变量模式中,有日本开发银行的多变量预测模型,中国学者周首华、杨济华的F分数模型,以及引入现金流量因素的预警模型等。
Z分数模型以其严谨的公式和较强的操作性被广泛应用。美国学者Edward I. Altman (1968)选取1946~1965年间的33家破产公司和33家正常经营的公司,提取出5种最具共同预测能力的财务比率,建立起类似于回归方程式的鉴别函数——Z分数模型 [2] 。其中,Z分数为五项财务指标的加权和,推荐以1.81为是否有破产危机的临界值,如果Z值低于1.81,则公司存在很大的破产危险。
目前我国学者对Z分数模型是否适用于国内企业存在争议。一派学者通过小规模数据验证ST公司的Z值小于1.81,认为该模型有效;另一派学者发现破产公司与非ST公司的Z值无明显分界,对Z分数模型持否定态度。但是这两派研究都存在数据规模较小、验证方式不够全面、未能从方法原理上进行分析等缺陷。
为此,本文首先归集了沪市上市公司2007~2013年913家财务报表数据,提取Z分数指标,按Z分数模型计算这些公司的Z值,对ST公司和非ST公司的Z值进行比对分析。研究发现ST公司和非ST公司的Z值呈现混杂分布的形态,两类公司间不具备线性可分的条件。这一结果表明:本质上为线性区分方法的Z分数模型在分析我国公司财务风险时存在方法上的缺陷。为了解决这一问题,本文在Z分数模型原有指标的基础上,提出了预测财务风险的决策树方法。研究发现,影响企业财务风险预警的主要财务指标有留存收益/总资产,营运资产/总资产和销售收入/总资产。实验结果表明,在非平衡数据状态下,提前三年预测公司是财务破产风险的准确率为75.37%,提前两年的预测准确率为88.54%;提前一年的预测准确率为95.45%。
本文共分为五个部分,第一部分引言,介绍背景意义。第二部分综述了国内学者对Z分数模型有效性的分歧。第三部分对Z分数模型有效性进行分析,实证Z分数模型对我国上市公司财务风险预警失效。第四部提出基于决策树的上市公司财务风险预警模型,并验证模型。第五部分,总结结论。
2. Z分数预警模型适用性分歧
Z分数模型的基本原理是用基于多重指标的线性多元函数识别有财务风险的公司。经典Z分数模型的表达式为:Z = 1.2X1 + 1.4X2 + 3.3X3 + 0.6X4 + 0.99X5。其中:Z为判别函数值;X1 = 营运资产/总资产;X2 = 留存收益/总资产;X3 = 息税前利润/总资产;X4 = 权益市Z场价值/负债账面总价值;X5 = 销售收入/总资产。奥特曼提出判断公司破产的临界值:若Z > 2.675,表明公司的财务状况良好,发生破产的可能性较小;若Z < 1.81,则公司存在很大的破产危险,即1.81是公司破产发生的定量界定。
目前,国内部分学者就Z分数模型对我国上市公司的财务风险预警是否有效进行了分析,主要存在两种观点:一些学者认为传统的Z分数模型仍适用于我国公司的财务风险预警,而另一些学者则对此持否定态度。
支持Z分数模型有效的研究方法有多种。向德伟(2002),张蔚虹,朱海霞(2012),王芳云(2005)通过计算几十家研究样本中ST公司的平均Z值和非ST公司的平均Z值,并与Z分数模型警戒值进行比较,发现ST公司平均Z值小于1.81,非ST公司平均Z值大于1.81,从而认为该实证研究大体上支持Z分数模型的有效性 [3] [4] [5] 。李艳(2012),常树春(2013)选取个别ST公司和非ST公司作为样本数据,对小规模样本数据Z值进行计算,发现3到5家非ST公司Z值大都低于1.81,得出Z分数模型有效结论 [6] [7] 。徐秀渠(2010)修改原Z分数模型的警戒值,使得样本数据的Z值落到修改后的相应预警区间内 [8] ;叶海英(2011)关注ST公司Z值,却忽略了非ST公司Z值是否落在相应预警区域内,仅从样本ST公司Z值小于1.81推出Z分数模型有效 [9] 。
同样,反对Z分数模型有效研究方法也有多种。周剑涛(2009),陈珍静(2011)通过研究几十家ST和非ST公司的财务数据,发现Z分数模型在验证我国上市公司中的破产公司时有较高的准确度,而作为预测非ST公司财务状况模型时,具有很大的误判性 [10] [11] 。张楚堂,杨志强(2009)把公司分成业绩优秀、业绩良好、业绩一般、业绩很差4类,用每一类公司整体的平均Z值判断,发现Z分数模型对业绩优良企业解释效果最好,对破产公司的解释效果最差 [12] 。邰丽娜(2011)通过选取沪深股市共193家公司2007年~2010年的财务数据,对每一年ST公司和非ST公司的Z值进行分析,发现Z模型对ST公司和非ST公司的准确率都不理想,得出Z分数模型并不适用于我国上市公司的财务风险预警 [13] 。
然而上述两派的研究方法都存在缺陷。首先,支持Z分数模型的主流研究方法是以ST公司和非ST公司的Z均值与预警临界值比较得出结论。虽然ST公司Z均值与非ST公司Z均值有所区别,但ST公司的Z值区间和非ST公司的Z值区间存在高度重叠,因此用Z均值的方法难以预判具体公司的财务风险水平。其次,在支持派别的研究方法中,个别样本数据选择过小,使得结论的可靠性降低。比如只选取3到5家ST公司验证,推出Z分数模型有效的结论。此外,有的研究方法只验证ST公司的Z值,而非ST公司的Z值能否与破产公司Z值区分开,无从得知。否定Z分数模型派别的主要理由是非ST公司和ST公司的Z值并没有明确的分界线,因此预测失效。否定派别的缺陷在于实验数据规模小,不具代表性,且仅呈现ST公司与非ST公司Z值无明显分界这一实验现象,既未从原理上解释原因,也未总结出规律和提出有效的解决方法。
3. 基于上市公司财报的Z分数模型有效性分析
在前人研究的基础上,本节以较大规模的样本数据集分析Z分数模型的有效性。最终获取了2007~2013年913家沪市上市公司的财务报表数据,同时判定ST公司和非ST公司的Z值,并进行分组区分和综合比较。分析结果表明:ST产公司与非ST公司的Z值线性不可分,因此采用Z分数模型预测我国公司财务风险时存在方法上的缺陷。
3.1. 数据准备
选取沪市913家上市公司2007年至2013年7年中每年被评为ST公司及非ST公司的财务数据作为数据样本,通过网上爬取的方式获得数据。为计算Z分数模型中的X1到X5五个指标,需要利润分配表、资产负债表、利润分配表摘要、股票成交概况、股本结构五大类报表。为获取每个公司在每一年是否被评为ST公司,需知每个公司每年的股票简称,该信息可通过金融界上企业的半年报列表获得。最终从金融界网站上爬取利润分配表、资产负债表、利润分配表摘要、半年报列表,从新浪财经上爬取股本结构,并从上海证券交易所爬取股票成交概况。爬取的这些报表均为网页,以html文件的形式存放在本地。通过分析不同网站不同类型财务报表数据的网页代码结构,编写数据抽取工具从本地的html文件中自动解析和抽取出每类报表中的财务指标数据存放到数据库中。最后,从这6张数据表中选取所需的财务指标计算X1到X5五个指标,并获取每个企业每年的ST标识,关联后得到建模数据表,至此数据准备过程完成。详细的数据基础如表1所示。
3.2. Z分数模型有效性实证分析
基于上述数据的分析结果表明:根据Z值大小判断一个企业是否有财务风险,并不能取得很好的效果。以2011年至2012年国内800多家沪市上市公司中每年被评为ST公司的企业和当年的非ST公司企业的财务数据作为样本,通过计算Z值发现Z分数模型并不能很好的区分ST公司和非ST公司企业。因2011年结果与2012年类似,图1仅展示了2012年Z分数模型的预测结果。图1中的X轴表示公司编号,Y轴表示Z-score值,红色表示ST公司,黑色表示非ST公司。
图1中完整呈现800多家上市公司的Z值,其中右上角子图进一步放大显示了Z值取值−1到5时相关企业的分布情况。可以看出ST公司和非ST公司在特征空间中交叉混杂分布,并不存在明确的分界线,例如按照Z = 1.81并不能区分ST公司和非ST公司。这一结果表明:ST公司与非ST公司的Z值是线性不可分的,本质上为线性区分方法的Z分数模型不能够分析国内企业的财务风险。
表2进一步对在Z值各区域ST公司和非ST公司的分布情况给出统计,更加完整地反映了Z分数模
Table 1. Overview of adopted data sets
表1. 数据基础统计表
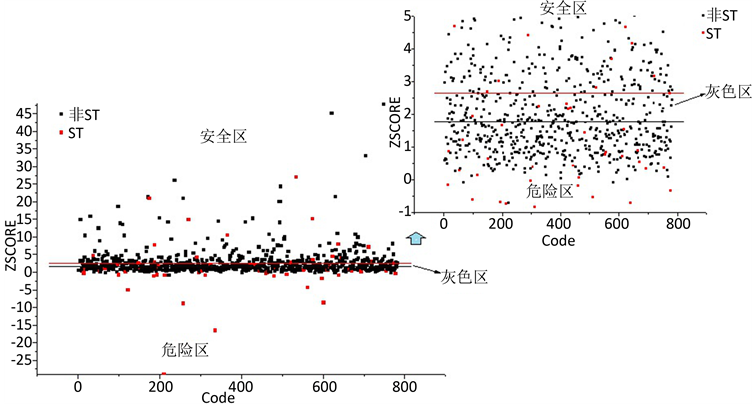
Figure 1. Prediction result of enterprise financial risk in 2012
图1. 2012年企业财务风险预测结果图
Table 2. Overview of prediction result of Z-Score model in 2012
表2. 2012年Z分数模型预测结果统计
型的失效情况。这里只对2012年做出说明,其他年份类似。从表2中统计得出,Z分数财务风险预警模型对我国上市公司的预测结果并不理想,要么准确率低要么覆盖率低,或者两者同时都低。2011年预测破产公司的准确率为13.38%,覆盖率为52.78%,2012年预测ST公司的准确率仅为9.92%,覆盖率为62.30%。
4. 基于决策树的财务风险预警模型
前述分析表明:传统的Z分数模型并不适用于我国上市公司的财务风险预警。因此,有必要探索更好的方法预测企业的财务风险。
数据挖掘中的分类算法能够从已知类别的历史数据中学习到一个模型,然后用该模型对未来未知类别的数据进行类别预测,符合对公司进行财务风险预警的场景,即通过对历史已知的是否有财务风险的公司样本的学习,预测未来的未知财务风险的公司样本是否有财务风险。同时,分类算法中有很多算法都能解决样本的线性不可分问题,这也弥补了前面提到的Z-score模型本质上只能解决线性可分问题的缺陷。
分类算法常用的有贝叶斯网络、支持向量机、决策树等。这些算法都能解决样本线性不可分的问题。但是贝叶斯、支持向量机等这些算法的模型结果的可解释性较差。J. Han. M. Kamber (2000)提出决策树算法从一组无次序、无规则的实例中推理出以决策树表示的分类规则,用这些规则来预测未知类别记录的类别 [14] ,这些规则可以将线性不可分的实例区分开。而且,通过这些规则使用者可以知道每一类的样本有什么特征,并可以从财务角度识别模型的合理性及指标的意义,解释性较好。
4.1. 基于决策树的财务风险预警模型
本节选择决策树算法对我国上市公司的财务风险进行预测。由于X1到X5这5个指标仍然能够反映公司的财务状况,因此构造决策树判定模型的目的是找出五项Z分数指标和企业是否存在财务风险间的关系,用它来预测风险未知的企业的类别。它将全部已知是否有财务风险的企业作为训练样本,将全部样本集作为初始节点S0,采用自顶向下的递归分裂方法,层层筛选出最优的Z-分数指标作为当前节点的分裂依据,形成新的分支节点Si,直至每个叶节点中的企业都属于同一类别为止。构建决策树判定模型的具体算法流程如下:
上市公司数据中ST与非ST样本数量存在明显的不平衡性,即正常公司的数量远多于破产公司的数量,例如2007~2013年国内上市公司财务数据中非ST公司是ST公司的11.7倍。这会对基于决策树算法的结果模型产生影响,使模型具有偏向性,具体表现为:对少数类的识别率远低于多数类的识别率。因此,我们采用非平衡数据和数据平衡2种方式构建决策树判定模型,然后通过对比两种方式的实验结果,选取比较合理且比较实用的方式。
第一种方式是在模型中保持数据原样,不对其进行平衡处理。建模选择2007年至2010年被评为ST的公司和当年的非ST公司作为训练集来训练决策树模型,用2011年至2013年被评为ST的公司和当年的非ST公司作为测试集来评价模型的好坏。而数据平衡方式是指对训练集数据作适当参数平衡,测试集数据仍保持原样。参数平衡是指在训练阶段,通过对不同类别的实例权重设置来改变数据的分布情况,在此模型中,就是通过复制较少类别(ST公司)的实例,以减少数据的不平衡程度。在训练阶段,经过多次试验得出,当ST公司的权重设为2,非ST公司的权重设为1时,得到的模型效果较好。用2007年至2010年被评为ST公司的企业和当年的非ST公司企业进行2倍参数平衡后作为训练集来训练决策树模型,用2011年至2013年被评为ST公司的企业和当年的非ST公司企业作为测试集来测试模型。非平衡数据下的决策数模型如图2所示,参数2倍平衡数据下的决策树模型与图2类似,不再赘述。
4.2. 基于决策树的财务风险预警模型规则解释
通过前述的决策树模型,可以得到判定破产的重要规则,模型规则如表3所示。
从未平衡数据和参数2倍平衡的两种模型结果来看,规则几乎是一致的。两种方式下的决策树的顶点都是以X2作为第一次的分裂指标,(如决策树图),下一个分裂指标为X1。由于未平衡数据状态下的规则与参数2倍平衡状态下的规则类似,因此仅对未平衡数据状态下的规则进行解释:
规则(1) “X2 ≤ −0.095且X1 ≤ −0.23→破产危机 = 是(188,90.0%,1)”表明:如果一个公司满足X2 ≤ −0.095并且X1 ≤ −0.23,那么此公司会被判断有破产危机,即有较高的财务风险;此次实验中188家破产公司中的90%都满足上述条件。规则中的X2 = 留存收益/总资产,留存收益是指企业从历年实现的利润中提取或留存于企业的内部积累,它来源于企业的生产经营活动所实现的净利润,该指标反映企业累积获利能力;X1 = 营运资产/总资产,营运资产 = 流动资产 − 流动负债,该指标反映企业的流动性,流动
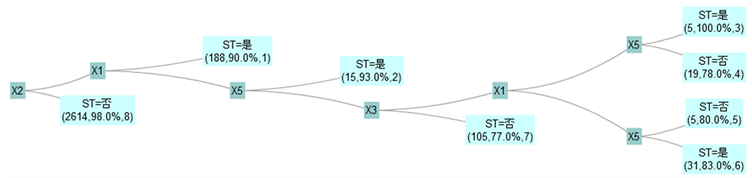
Figure 2. Decision tree under the imbalanced data
图2. 非平衡数据状态下的决策树
Table 3. Rules of model for financial risk judgment
表3. 判定财务风险的模型规则
资本越多,说明不能偿债的风险越小。也就是说,在国内现行条件下,当一个公司留存收益/总资产 ≤ −0.95%时,即积累利润已经亏空并且亏空大于总资产的9.5%,同时企业在短期经营中已经资不抵债,流动负债超过流动资产的金额达到总资产的23%时,这个企业很可能面临财务危机。
规则(2) “X2 ≤ −0.095且X1 > −0.23且X5 ≤ 0.10→破产危机 = 是(15,93.0%,2)”表明:如果一个公司满足X2 ≤ −0.095,X1 > −0.23,并且X5 ≤ 0.10,那么此公司会被判定有破产危机。当一个公司留存收益/总资产≤ −0.95%时,即积累利润已经亏空并且亏空大于总资产的9.5%,即便X1 (营运资产/总资产) > 临界值−23%时,仍要继续判断X5 = 销售收入/总资产是否小于10%。也就是说即便一个公司在亏空不超过总资产9.5%,流动性也还可以的时候,如果销售收入跟不上(不到总资产10%),那么这个公司也有很大可能陷入较高的财务风险。
其他规则以此类推。由上述模型结果得出:最重要的判定指标是X2 = 留存收益/总资产,X1 = 营运资产/总资产,和X5 = 销售收入/总资产。并可得出,决策树模型判定的规律是,首先判断公司留存收益的亏空程度,再判断其短期流动性,继而判断其销售收入与公司规模的符合程度,一般情况下,亏空不高于总资产的10%,流动负债超过流动资产的金额不高于总资产的23%,销售收入不低于总资产的10%。如果一个公司亏空大,且流动性差,那么很有可能面临财务危机;如果一个公司亏空大,销售收入跟不上,即便流动性较好,也很有可能陷入财务危机。
4.3. 基于决策树的财务风险预警模型验证
对于非平衡数据模型和数据平衡模型,我们都选择相同的测试集,即2011~2013年上市公司的财务数据来检验模型,检验结果如表4所示。
在非平衡数据状态下,从模型验证结果表4可以得出,提前三年预测无破产危机公司的准确率和覆盖率都达95%以上。对于有破产危机公司的预测,在准确率上表现较理想,维持在75%以上的水平,在覆盖率上稍差一些,维持在60%左右。提前一年预测破产公司的财务风险的准确率为95.45%,覆盖率为
Table 4. Prediction result of decision tree under balanced and imbalanced data with the duplicated rare instances
表4. 参数2倍平衡与非平衡数据状态下决策树预测结果
58.33%;提前2年预测的准确率为88.54%,覆盖率为63.91%;提前3年预测的准确率为75.37%,覆盖率为63.52%。在参数平衡数据状态下,从表4的模型验证结果看出,结果与非平衡数据状态下类似,在未来三年内的无破产危机公司的预测都比较准确,准确率和覆盖率都达95%以上。而对于有破产危机公司的预测,数据2倍平衡下的结果比数据非平衡下的结果略胜一筹。虽然准确率要比非平衡数据的结果稍差一些,但在覆盖率上能达到70%以上。提前1年预测破产的准确率为75.71%,覆盖率为73.61%;提前两年预测破产的准确率为75.74%,覆盖率为77.44%;提前三年预测破产的准确率为62.63%,为74.84%。总体看来,在参数2倍平衡状态下的模型在准确率和覆盖率两方面表现更均衡一些,但值得注意的是,随着预测年份的推移,两种模型的准确度都有所下降。
5. 总结
通过对传统Z分数模型有效性实证分析,发现国内有破产危机的公司与正常公司Z值本身的非线性可分性,因此基于多元线性回归函数的Z分数模型的预测效果并不理想,已不能完全反映当代国内企业的财务风险与危机。
基于决策树算法的财务风险预警模型为我国公司的财务风险预警提供了一种有效的方法。它有能力解决有破产危机的公司与正常公司的非线性可分的特点。它可根据所要预测的年份选择最近的数据进行训练,以保证模型跟进现行市场变化,也可根据模型规则判断财务风险的关键领域及风险程度。该模型在非平衡数据与参数2倍平衡数据状态下的模型都表现良好,后者在准确率和覆盖率两项的表现上更为均衡。在两种方式下,对正常公司的判定准确率和覆盖率都能达95%以上,对有破产危机的公司的判断准确率和覆盖率几乎都能达75%以上。值得注意的是,虽然决策树模型能较为准确的预判公司是否面临财务风险,并且通过指标可以判断所面临财务风险的程度,但随着时间的推移,模型准确率会有所下降。因此预判公司是否有财务风险时,需要选择近几年的数据做训练。这样训练出的模型才符合实情,也能提高模型的精确性。
基金项目
国家科技支撑计划项目《面向国家审计“免疫系统”的审计模拟与仿真平台研发及应用示范》(批准号:2012BAH08B02),国家自然科学基金项目《基于社会计算的社会保障国家审计政策功能研究》(批准号:71272216)。
文章引用
杨蕴毅,孙中和,卢 靖. 基于Z-Score指标决策树的财务风险预警模型研究
Financial Risk Early Warning Model of Decision Tree Research Based on Z-Score Indicators[J]. 现代管理, 2017, 07(05): 185-193. http://dx.doi.org/10.12677/MM.2017.75026
参考文献 (References)
- 1. 常树春, 范文雨. 基于Z-score模型的汽车行业上市公司财务风险实证分析[J]. 商业会计, 2013(13): 89-91.
- 2. 陈珍静. Z-score模型在我国上市公司财务预警中适用性的探讨——基于交通运输设备制造业的实证分析[J]. 国际商务财会, 2011(4): 60-63.
- 3. 胡剑. 论企业财务风险的防范[J]. 会计师, 2014(4x): 47-48.
- 4. 李艳. 基于Z-Score模型对我国社会服务业上市公司破产预测的实证分析[J]. 商, 2012(7): 84, 109.
- 5. 邰丽娜. Atman’s Z-score模型对我国上市公司的适用性分析[J]. 财会研究, 2011(24): 49-51.
- 6. 王芳云. 运用Z计分模型对上市公司财务风险的实证研究[J]. 山东纺织经济, 2005(5): 42-44.
- 7. 向德伟. 运用“Z记分法”评价上市公司经营风险的实证研究[J]. 会计研究, 2002(11): 53-57.
- 8. 徐秀渠. Altman’s Z-Score模型在企业风险管理中的应用研究[J]. 经济经纬, 2010(4): 103-106.
- 9. 叶海英. 对上市公司财务预警的实证研究——Z计分模型[J]. 中国外资, 2011(24): 84-85.
- 10. 张楚堂, 杨志强. 基于Z-score模型的国有公司财务分析[J]. 武汉理工大学学报, 2009(15): 145-149.
- 11. 张蔚虹, 朱海霞. Z-Score模型对科技型上市公司财务风险预警的适用性检验[J]. 科技管理研究, 2012, 32(14): 228-231.
- 12. 周剑涛, 庞文凤. Z-SCORE财务预警模型在上市公司应用的实证研究[J]. 财会通讯, 2009(24): 25-27.
- 13. Altman, I.E. (1968) Financial Ratios Discriminant Analysis and the Prediction of Corporate Bankruptcy. Journal of Finance, 4, 589-609.
- 14. Han. J. and Kamber, M. (2000) Data Mining: Concepts and Techniques.
