Pure Mathematics
Vol.4 No.03(2014), Article
ID:13551,8
pages
DOI:10.12677/PM.2014.43012
Stability Analysis of Uncertain Sampled-Data Systems
School of Mathematical Sciences, Inner Mongolia University, Hohhot
Email: jiarong0719@126.com, gaocx0471@163.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Mar. 6th, 2014; revised: Apr. 8th, 2014; accepted: Apr. 16th, 2014
ABSTRACT
This paper deals with the stability of linear time-invariant impulsive system with feedback control. The pulses, at some time in the past, were the important factor causing system instability. Here, we first regard the impulsive system as a special reset system, then we analyze the stability of sampled-data system, and design reset matrices such that the uncertain sampled-data system is stable. Based on the classical Lyapunov method and linear matrix inequality LMI form, the necessary and sufficient conditions for stability are given. At last, we apply the results to the uncertain LTI sampled-data systems and illustrate a numerical example.
Keywords:Impulsive System, Reset Design, Sampled-Data System, Stability, Lyapunov Functions, Polytopic Embedding

不确定采样数据系统的稳定性分析
贾 荣,高彩霞
内蒙古大学数学科学学院,呼和浩特
Email: jiarong0719@126.com, gaocx0471@163.com
收稿日期:2014年3月6日;修回日期:2014年4月8日;录用日期:2014年4月16日

摘 要
本文主要研究了具反馈控制的线性时不变脉冲系统的稳定性问题。在过去的理论中认为,脉冲是造成系统不稳定的重要因素。在这里,我们将脉冲系统看作特殊的重置系统,继而得到,在适当的脉冲作用下,系统不但能保持原来的稳定性,甚至可以使一个原来不稳定的系统变得稳定。本文以经典的Lyapunov方法为基础,以线性矩阵不等式LMI为表达形式,给出使系统平衡点全局一致指数稳定的充分必要条件。并以此为基础,对不稳定的微分控制系统,给出使系统指数稳定的脉冲重置的设计方法及重置矩阵的形式。文章最后将结果运用到不确定的LTI采样数据系统中,并给出算例。
关键词
脉冲系统,重置设计,采样数据系统,稳定性,Lyapunov函数,多面体嵌入

1. 引言
脉冲微分方程展示的是由经典的常微分方程描述的连续过程和由差分方程描述的瞬间状态跳跃的离散过程相结合的数学模型[1] [2] ,这样的跳跃脉冲可以被看做重置系统。可以通过设计重置法则来使系统达到稳定。采样数据系统是一类由电子装置控制的重置系统[3] [4] 。在过去的十几年中受到了广泛的关注,用于建立其稳定性的方法也多种多样。其中,文献[5] [6] 基于Lifting方法讨论其稳定性,但这种方法一般不适用于采样区间不确定的系统;文献[7] [8] 从具时滞的控制角度出发,将闭环系统扩展为无限维的时滞微分方程,基于Razumikin技术建立了采样数据系统的稳定性;此外,在采样周期时变的情况下,文献[9] 基于Lyapunov函数法建立了采样数据系统的稳定性。
本文研究了具反馈控制的线性时不变脉冲系统的稳定性问题。将脉冲系统看作特殊的重置系统,我们得到,在脉冲作用下,系统能保持原来的稳定性,甚至可以使一个原来不稳定的系统在脉冲的作用下而稳定。我们以经典的Lyapunov方法为基础,以线性矩阵不等式(LMIs)的形式给出使系统平衡点全局一致指数稳定的充分必要条件。并以此为基础,对不稳定的微分控制系统,给出使系统指数稳定的脉冲重置的方法及重置矩阵的形式。这些结果对于利用脉冲对一个系统进行镇定具有较大意义。文章最后将结果运用到不确定的LTI采样数据系统。并给出算例。与之前的理论[9] [10] 相比,本文所研究的第一个重要不同在于,重置区间被认为是不确定的,在近似周期的情况下,如何保证系统的稳定;第二个大胆的创新是,在采样的瞬间,给予系统一个适合的刺激(脉冲)来使整个系统稳定。
2. 预备知识
大多数的采样数据系统,是由一个具反馈控制的线性时不变微分系统描述的,其中,恒定增益K将采样器与保持器连接在一起。这一过程由如下形式表示:
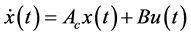
其中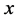 ,
, 分别表示该过程的状态和输入控制。在采样时间
分别表示该过程的状态和输入控制。在采样时间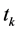 ,
, ,抽出的状态
,抽出的状态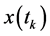 被发送给控制器,经过加工变为
被发送给控制器,经过加工变为 ,然后被送回系统中,直到到达下一个控制命令更新。在采样瞬间,给系统一个适当的刺激(脉冲)。这样的系统可以被描述为具分段常值控制的线性重置系统,如下:
,然后被送回系统中,直到到达下一个控制命令更新。在采样瞬间,给系统一个适当的刺激(脉冲)。这样的系统可以被描述为具分段常值控制的线性重置系统,如下:
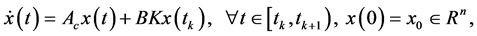 (1)
(1)
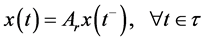 (2)
(2)
其中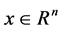 代表系统状态,时间
代表系统状态,时间 。矩阵
。矩阵 ,
,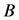 ,
,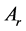 为适合维数的常值矩阵。
为适合维数的常值矩阵。
 (3)
(3)
为重置时间集。我们记
 (4)
(4)
为采样区间长度,对于所有的 ,
, 属于紧集
属于紧集 ,
,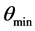 和
和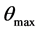 分别表示
分别表示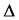 中的最大值和最小值。
中的最大值和最小值。 代表可行序列
代表可行序列 的集合,
的集合, 。
。
 (5)
(5)
我们假定,对任意的 重置系统(1)和(2)存在唯一解。在时刻
重置系统(1)和(2)存在唯一解。在时刻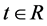 ,以
,以 为初始状态,
为初始状态,
并在重置序列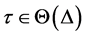 的作用下,解表示为
的作用下,解表示为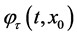 。它可以写为
。它可以写为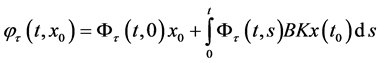
其中,转移矩阵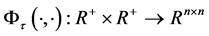 符合以下关系:
符合以下关系:
 (6)
(6)
 (7)
(7)
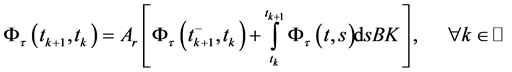 (8)
(8)
在上面的方程中,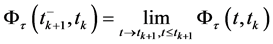 。注意到系统状态在重置时刻之间是线性时间不变的,因此,该转移矩阵对所有
。注意到系统状态在重置时刻之间是线性时间不变的,因此,该转移矩阵对所有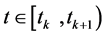 ,可以明确表示为
,可以明确表示为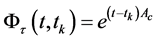 。
。
接下来的研究是基于以下的积分运算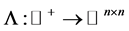
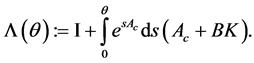 (9)
(9)
算子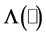 关于
关于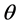 连续,
连续,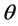 属于紧集
属于紧集 。因此,该转移矩阵
。因此,该转移矩阵
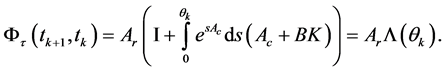
定义1.1. 称系统(1)和(2)的平衡点 是关于重置序列
是关于重置序列 全局一致指数稳定(GUES)的,如果存在正数
全局一致指数稳定(GUES)的,如果存在正数 ,使得对任意的
,使得对任意的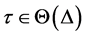 ,
,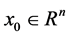 和
和 ,都有
,都有
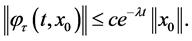 (10)
(10)
关于系统的稳定性分析,本文将解决以下两个问题:
问题1:假定常数矩阵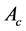 ,
,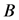 ,
, 和
和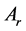 给定。提供判断系统(1)和(2)的平衡点
给定。提供判断系统(1)和(2)的平衡点 是全局一致指数稳定的可行条件,并以线性矩阵不等式
是全局一致指数稳定的可行条件,并以线性矩阵不等式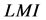 的形式给出。
的形式给出。
问题2:假定常数矩阵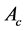 ,
,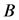 和
和 给定。设计合适的重置矩阵
给定。设计合适的重置矩阵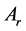 ,以保证系统(1)和(2)的平衡点
,以保证系统(1)和(2)的平衡点 的稳定性。
的稳定性。
3. 主要结果
3.1. 稳定性分析
在本节将给出指数稳定的条件,以解决以上问题1。
在提供 稳定性条件之前,首先给出所考虑的脉冲系统的稳定性。运用在重置时间的离散模型,可以推导出指数稳定的充分必要条件。该分析利用了一类在紧集上满足线性微分包含的拟二次Lyapunov函数[10] [11] 。更确切地说,我们使用形如
稳定性条件之前,首先给出所考虑的脉冲系统的稳定性。运用在重置时间的离散模型,可以推导出指数稳定的充分必要条件。该分析利用了一类在紧集上满足线性微分包含的拟二次Lyapunov函数[10] [11] 。更确切地说,我们使用形如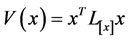 的函数,其中
的函数,其中 为依赖于系统状态的Lyapunov矩阵,并满足齐次性,即
为依赖于系统状态的Lyapunov矩阵,并满足齐次性,即
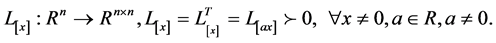
下面的定理表明,这样的函数在重置点的下降性保证了重置系统的稳定性。
定理1:考虑重置系统(1)和(2),其中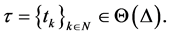 平衡点
平衡点 是全局一致指数稳定的当且仅当存在一个严格凸的正定函数
是全局一致指数稳定的当且仅当存在一个严格凸的正定函数
 (11)
(11)
且具备齐次性质,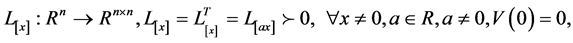 对所有的
对所有的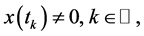 以及任何可行重置序列
以及任何可行重置序列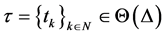 ,满足
,满足
 (12)
(12)
证明 首先,因为参数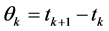 属于紧集
属于紧集 ,因此,对于任何序列
,因此,对于任何序列 和任意的
和任意的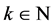 ,转移矩阵
,转移矩阵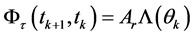 关于
关于 连续。因此,在重置时间,系统(1)和(2)的解决可以由一个线性微分包含描述:
连续。因此,在重置时间,系统(1)和(2)的解决可以由一个线性微分包含描述:
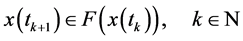 (13)
(13)
其中,
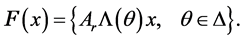 (14)
(14)
回顾文献[10] 中全局一致指数稳定的概念,由线性微分包含(13)可以推出以下事实:
存在常数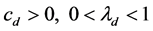 ,使得
,使得
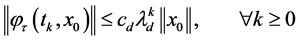 (15)
(15)
对于所有的初始条件的 ,以及
,以及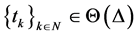 成立,当且仅当存在函数
成立,当且仅当存在函数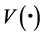 ,满足不等式(12)。现在我们只需证明,在重置时间的指数稳定性等价于所有
,满足不等式(12)。现在我们只需证明,在重置时间的指数稳定性等价于所有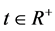 的指数稳定性,即:式(10)⇔式(15)。证明如下。
的指数稳定性,即:式(10)⇔式(15)。证明如下。
假设重置系统(1)和(2)是指数稳定的,由式(10),因为 ,当取
,当取 和
和 时,(15)成立。
时,(15)成立。
假设关系式(15)成立。由于对所有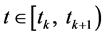 ,有
,有 ,且转移矩阵
,且转移矩阵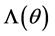 关于有界,即存在
关于有界,即存在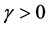 ,使得
,使得
 (16)
(16)
因此,对所有的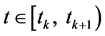 ,有
,有 。此外,对任意的
。此外,对任意的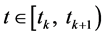 和
和 ,我们有
,我们有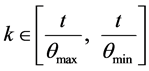 ,这就意味着,当
,这就意味着,当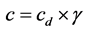 和
和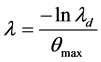 时,关系式(10)成立。
时,关系式(10)成立。
下面的定理在拟二次Lyapunov函数存在的基础上,给出了具有重置法则(2)的闭环系统(1)的稳定性的充分条件。
定理2:考虑系统(1)和(2), 属于如(5)中描述的可行重置序列集
属于如(5)中描述的可行重置序列集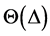 。假设矩阵
。假设矩阵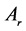 给定。如果存在矩阵
给定。如果存在矩阵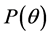 ,
, ,且关于
,且关于 连续,
连续, ,以及矩阵
,以及矩阵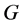 ,对所有
,对所有 以及如(9)所述的
以及如(9)所述的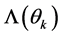 满足以下线性矩阵不等式:
满足以下线性矩阵不等式:
 (17)
(17)
则存在如定理1满足条件(12)的拟二次Lyapunov函数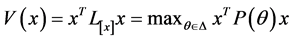 ,也就是系统(1)和(2)的平衡点
,也就是系统(1)和(2)的平衡点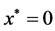 是全局一致指数稳定的。
是全局一致指数稳定的。
证明 这里需要证明,如果条件(17)成立,则系统(1)和(2)的平衡的点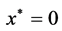 是全局一致指数稳定的。假设对所有
是全局一致指数稳定的。假设对所有 ,存在矩阵
,存在矩阵 和
和 满足条件(17)。由于
满足条件(17)。由于 关于
关于 连续,且
连续,且 被定义在一个紧集上,那么
被定义在一个紧集上,那么 相对于
相对于 的像是紧集。因此对任意
的像是紧集。因此对任意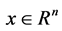 ,有
,有
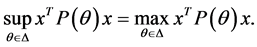
考虑Lyapunov矩阵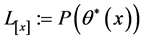 ,其中
,其中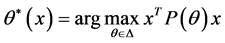 。对于任何正数
。对于任何正数 ,
,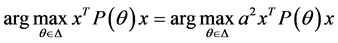 。这意味着
。这意味着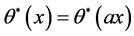 ,即
,即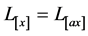 。这表明,
。这表明, 是二阶齐次函数。其凸性是也很容易证明。
是二阶齐次函数。其凸性是也很容易证明。
因此,我们可选择的拟二次Lyapunov函数形如:
 (18)
(18)
它满足定理1所需的凸性和齐次性条件。如文献[12] ,在不等式(17)左乘

同时右乘它的转置,则有下面不等式成立:
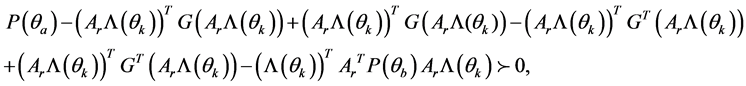 (19)
(19)
即对 ,有
,有
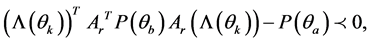 (20)
(20)
继而对于任意的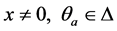 ,有
,有
 . (21)
. (21)
那么,对于任何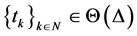 ,
,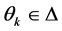
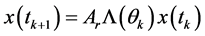 . (22)
. (22)
由(20)~(22)下列关系式对于任意的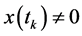 ,
,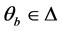 有
有
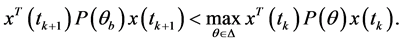 (23)
(23)
需要注意的是
 . (24)
. (24)
关系式(23)适用于任何 ,因此当
,因此当 也同样成立。如(18)给出的
也同样成立。如(18)给出的 的定义,对所有的
的定义,对所有的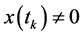 ,我们推出
,我们推出
 (25)
(25)
这就说明存在一个满足定理1的条件的函数。
3.2. 脉冲重置设计
在本节将给出问题2的解决方法。即给出使系统(1)稳定的重置系统(2)中重置矩阵的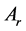 的设计方法。该方法是基于重置受限的情况下,因为可能只有部分系统变量会经历跳跃。为了阐明稳定问题的假设,我们记
的设计方法。该方法是基于重置受限的情况下,因为可能只有部分系统变量会经历跳跃。为了阐明稳定问题的假设,我们记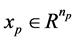 为连续状态变量,
为连续状态变量,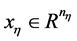 为可能经历重置的变量。显然,该系统状态应该满足
为可能经历重置的变量。显然,该系统状态应该满足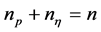 。不失一般性,假系统(1)的状态形如
。不失一般性,假系统(1)的状态形如 。而使我们感兴趣的是:
。而使我们感兴趣的是:
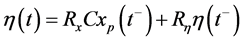 (26)
(26)
其中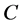 为适当维数的常矩阵,
为适当维数的常矩阵,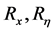 是将要设计的矩阵。为将约束(26)表示为形如(2)的形式,记:
是将要设计的矩阵。为将约束(26)表示为形如(2)的形式,记:
 (27)
(27)
下面的定理证明了如何用定理2的方法推导出形如(26)的重置矩阵。
定理3:考虑系统(1)以及重置控制(26),与其相关联的重置矩阵形如(27)。此外,考虑取值与如(5)描述的重置序列集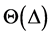 的序列
的序列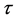 。如果存在矩阵
。如果存在矩阵 ,
,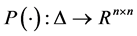 ,关于
,关于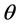 连续,且
连续,且 ,以及适当维数的
,以及适当维数的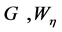 和
和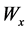 ,对所有
,对所有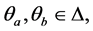 满足以下线性矩阵不等式
满足以下线性矩阵不等式
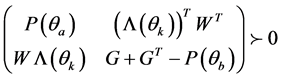 (28)
(28)
其中,
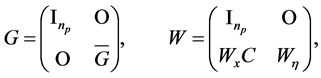 (29)
(29)
那么闭环系统(1),(26)和(27)的平衡点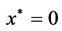 全局一致指数稳定,其中,
全局一致指数稳定,其中,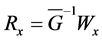 ,
, 。
。
证明 假设存在对称正定矩阵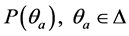 ,和满足条件(28)的形如式(29)的矩阵
,和满足条件(28)的形如式(29)的矩阵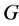 和
和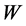 。那么
。那么 也是正定的,这意味着
也是正定的,这意味着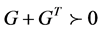 ,即
,即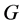 是可逆的。现在考虑
是可逆的。现在考虑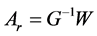 。由
。由 ,及不等式(28),对
,及不等式(28),对 有:
有:
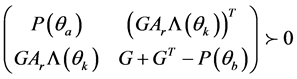 (30)
(30)
这使能够证明以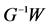 为重置矩阵的系统(1)和(2)的指数稳定性(应用定理2)。由式(29)给出的
为重置矩阵的系统(1)和(2)的指数稳定性(应用定理2)。由式(29)给出的 和
和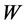 使得
使得 具有以下形式:
具有以下形式:
 (31)
(31)
其中 ,
, 。
。
3.3. 算例
考虑如系统(1)所述的采样数据控制,其中:

保证系统(1)稳定性的最大恒定的采样时间间隔,在文献[9] 中给出的是1.3277(图1)。当采样间隔不再恒定,在文献[13] -[15] 提供了保证稳定性的采样间隔上界为0.8696。在文献[16] ,被提高到0.8871,文献[9] 又上升为1.1137(图2)。因此可以看出,相比于恒定采样间隔,变化的采样区间将导致区间长度的值更保守。这是合理的,因为需要保证系统在不同采样间隔下都能达到稳定的。
在本文中,利用定理3.3.1,我们可以对 的长度进行估计,使得尽管重置间隔是变化的,也能保证系统是稳定的。我们算出满足条件的θ = 2.21。而当θ = 2.21,在没有重置的情况下,该系统是不稳定的(图3)。同时,利用定理我们可以计算出
的长度进行估计,使得尽管重置间隔是变化的,也能保证系统是稳定的。我们算出满足条件的θ = 2.21。而当θ = 2.21,在没有重置的情况下,该系统是不稳定的(图3)。同时,利用定理我们可以计算出
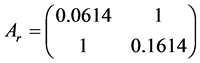
最后得出,在重置矩阵的作用下,当采样间隔最大化到θ = 2.21时,系统依然保持稳定(图4)。这是很好的结果。
4. 结论
本文研究了具反馈控制的线性时不变脉冲系统的稳定性问题。将脉冲系统看作特殊的重置系统,我们得到,在脉冲作用下,系统能保持原来的稳定性,甚至可以使一个原来不稳定的系统在脉冲的作用下而稳定。我们以经典的Lyapunov方法为基础,以线性矩阵不等式(LMIs)的形式给出使系统平衡点全局一

Figure 1. Constant sampling interval 1.3277
图1. 最大恒定采样间隔1.3277
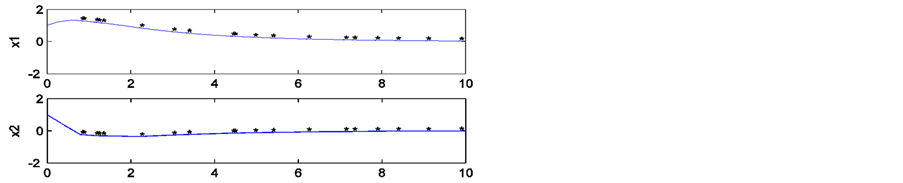
Figure 2. Varying sampling interval [0 1.1137]
图2. 最大变化采样间隔[0 1.1137]

Figure 3. Unstable without reset
图3. 无重置情况下,系统不能稳定

Figure 4. Stable without reset
图4. 重置后系统保持稳定
致指数稳定的充分必要条件。并以此为基础,对不稳定的微分控制系统,给出使系统指数稳定的脉冲重置的方法及重置矩阵的形式。
致 谢
作者衷心感谢导师高彩霞副教授的悉心指导和热心鼓励,感谢中国自然科学基金(基金编号:11261033)的资助。向给予转载和引用权的资料,文献,研究思想和设想的所有者,表示感谢。感谢审稿人的审稿意见。
基金项目
中国自然科学基金(基金编号:11261033)。
参考文献 (References)
- [1] Lakshmikantham, V., Banov, D.D. and Simeonov, P.P.S. (1989) Theory of impulsive differential equations. World Scientific, Singapore.
- [2] Yang, T. (2001) Impulsive control theory. Springer, Berlin.
- [3] Unbehauen, I.R. and Cichocki, I.A. (1989) Fundamentals of sampled-data systems. In: MOS Switched-Capacitor and Continuous-Time Integrated Circuits and Systems, Springer, Berlin, 1-82.
- [4] Chen, T., Francis, B. and Hagiwara, T. (1998) Optimal sampled-data control systems. Proceedings of the IEEE, 86, 741-741.
- [5] Bamieh, B., Pearson, J.B., Francis, B.A. and Tannenbaum, A. (1991) A lifting technique for linear periodic systems with applications to sampled-data control. Systems & Control Letters, 17, 79-88.
- [6] Longo, S., Herrmann, G. and Barber, P. (2010) Stabilisability and detectability in networked control. Control Theory & Applications, IET, 4, 1612-1626.
- [7] Liu, K. and Fridman, E. (2012) Wirtingers inequality and lyapunov-based sampled-data stabilization. Automatic, 48, 102-108.
- [8] Fridman, E. (2010) A refined input delay approach to sampled-data control. Automatica, 46, 421-427.
- [9] Naghshtabrizi, P., Hespanha, J.P. and Teel, A.R. (2008) Exponential stability of impulsive systems with application to uncertain sampled-data systems. Systems & Control Letters, 57, 378-385.
- [10] Hetel, L., Kruszewski, A., Perruquetti, W. and Richard, J. (2011) Discrete and inter-sample analysis of systems with aperiodic sampling. IEEE Transactions on Automatic Control, 56, 1696-1701.
- [11] Molchanov, A.P. and Pyatnitskiy, Y.S. (1989) Criteria of asymptotic stability of differential and difference inclusions encountered in control theory. Systems & Control Letters, 13, 59-64.
- [12] de Oliveira, M.C., Bernussou, J. and Geromel, J.C. (1999) A new discrete-time robust stability condition. Systems & Control Letters, 37, 261-265.
- [13] Naghshtabrizi, P. and Hespanha, J.P. (2005) Designing an observer-based controller for a network control system. 44th IEEE Conference on Decision and Control, 12-15 December 2005, 848-853.
- [14] Fridman, E., Seuret, A. and Richard, J.P. (2004) Robust sampled-data stabilization of linear systems: An input delay approach. Automatica, 40, 1441-1446.
- [15] Yue, D., Han, Q.L. and Peng, C. (2004) State feedback controller design of networked control systems. IEEE Transactions on Circuits and Systems II: Express Briefs, 51, 640-644.
- [16] Yue, D., Han, Q.L. and Lam, J. (2005) Network-based robust h control of systems with uncertainty. Automatica, 41, 999-1007.