Pure Mathematics
Vol.4 No.06(2014), Article
ID:14309,5
pages
DOI:10.12677/PM.2014.46032
Moment Consistency of Kernel Regression Estimation for Random Design
Department of Mathematics, Guilin University of Aerospace Technology, Guilin
Email: xinyang_emily@sina.cn
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Sep. 19th, 2014; revised: Oct. 15th, 2014; accepted: Oct. 20th, 2014
ABSTRACT
For the nonparametric regression model with random design, we discuss the Nadaraya-Watson type kernel regression estimator for 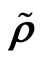 mixing samples, and prove the point moment consistency and the global moment consistency of the kernel regression estimator. The obtained results generalize the Devroye’s (1981) conclusions.
mixing samples, and prove the point moment consistency and the global moment consistency of the kernel regression estimator. The obtained results generalize the Devroye’s (1981) conclusions.
Keywords:Random Design, 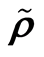 Mixing Sample, Kernel Regression Estimator, Moment Consistency
Mixing Sample, Kernel Regression Estimator, Moment Consistency

随机设计核回归估计的矩相合性
杨 昕
桂林航天工业学院数理部,桂林
Email: xinyang_emily@sina.cn
收稿日期:2014年9月19日;修回日期:2014年10月15日;录用日期:2014年10月20日

摘 要
对随机设计非参数回归模型,在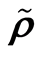 混合样本下研究Nadaraya-Watson型核回归估计,证明了这种核回归估计的逐点矩相合性和全局矩相合性,所获结果推广了Devroye (1981)的结论。
混合样本下研究Nadaraya-Watson型核回归估计,证明了这种核回归估计的逐点矩相合性和全局矩相合性,所获结果推广了Devroye (1981)的结论。
关键词
随机设计,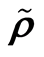 混合样本,核回归估计,矩相合性
混合样本,核回归估计,矩相合性

1. 引言
设X是d维随机向量,Y是一维随机变量。如果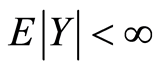 ,则回归函数
,则回归函数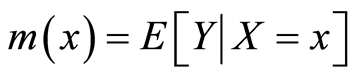 存在。对于来自总体
存在。对于来自总体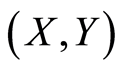 的一组样本
的一组样本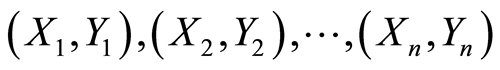 ,Nadaraya (1964, 1965) [1] [2] 和Watson [3] (1964)提出了如下核回归估计
,Nadaraya (1964, 1965) [1] [2] 和Watson [3] (1964)提出了如下核回归估计
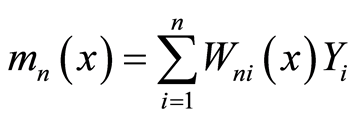 , (1.1)
, (1.1)
其中
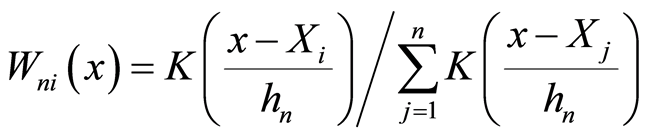 , (1.2)
, (1.2)
 为核函数,
为核函数,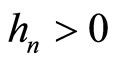 为窗宽。这种估计通常称为随机设计的NW核回归估计。
为窗宽。这种估计通常称为随机设计的NW核回归估计。
关于随机设计的NW核回归估计的相合性质,有许多学者做过研究。Devroye and Wagner [4] 于1980年在独立样本条件下证明了NW核回归估计的全局矩相合性,并将结果应用于证明相应的判别分析的Bayes风险的相合性。Devroye [5] (1981)进一步讨论了这种核回归估计的逐点矩相合性和全局矩相合性,以及强相合性。Greblicki et al. [6] (1984)证明NW核回归估计的弱相合性,并在Y有界的条件下证明了该估计的强相合性。Nze et al. [7] (2002)在一类弱相依样本下讨论NW核回归估计和相应的Boostrap估计的渐近性质,如渐近方差、渐近正态性、强相合性及其收敛速度。本文将在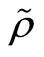 混合样本下研究NW核回归估计的逐点矩相合性和全局矩相合性,所获结果推广了Devroye [5] (1981)的结论。
混合样本下研究NW核回归估计的逐点矩相合性和全局矩相合性,所获结果推广了Devroye [5] (1981)的结论。
2. 主要结论
我们首先明确 混合的定义。设
混合的定义。设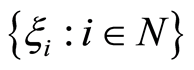 是概率空间
是概率空间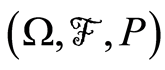 中的随机变量序列(其中N为全体自然数集),
中的随机变量序列(其中N为全体自然数集),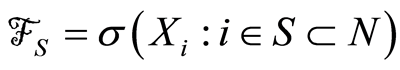 为σ-域。对F中任意两个子σ-域A和B,令
为σ-域。对F中任意两个子σ-域A和B,令
 . (2.1)
. (2.1)
Bradley [8] [9] (1990, 1992)引进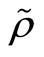 混合系数:对
混合系数:对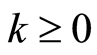 ,令
,令
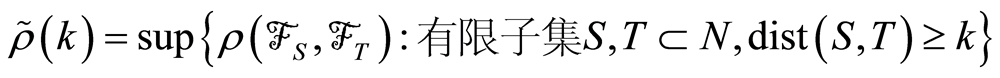 . (2.2)
. (2.2)
如果存在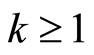 使得
使得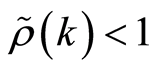 ,则称随机变量序列
,则称随机变量序列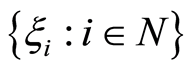 是
是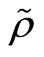 混合的。
混合的。
我们需要如下假设
(A1)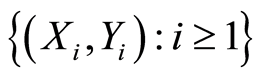 为
为 混合的随机向量序列,且
混合的随机向量序列,且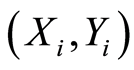 与
与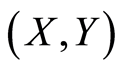 同分布。
同分布。
(A2) 存在正常数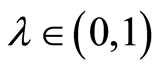 ,使得
,使得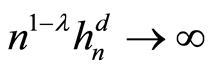 (当
(当 时),其中d为随机向量X的维数。
时),其中d为随机向量X的维数。
(A3) 存在正常数 ,
,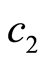 和r,使得
和r,使得
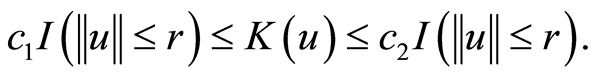
本文将使用缩写“![]() ”表示结论“对
”表示结论“对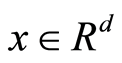 关于测度
关于测度![]() 几乎处处”成立,并用
几乎处处”成立,并用 表示随机变量X的概率测度。
表示随机变量X的概率测度。
定理1:设条件(A1)~(A3)成立。如果 (其中
(其中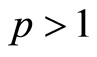 ),则
),则
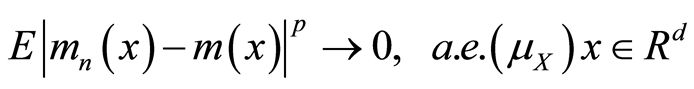 . (2.3)
. (2.3)
定理2:在定理1的条件下,有
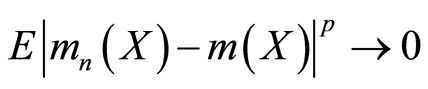 . (2.4)
. (2.4)
3. 定理的证明
为了证明定理的结论,我们需要下面几个引理。
引理1([4] , Lemma 1.1):设![]() 表示在
表示在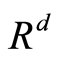 中以x为中心r为半径的闭球。如果
中以x为中心r为半径的闭球。如果![]() ,即
,即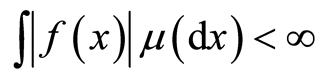 ,则当
,则当![]() 时,有
时,有
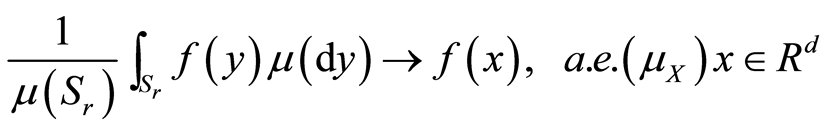 . (3.1)
. (3.1)
引理2([4] , Lemma 2.2):设![]() 表示在
表示在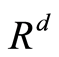 中以x为中心r为半径的闭球,则存在关于测度
中以x为中心r为半径的闭球,则存在关于测度![]() 几乎处处有限的非负函数
几乎处处有限的非负函数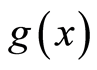 ,使得当
,使得当![]() 时
时
![]() . (3.2)
. (3.2)
从而,如果当 时
时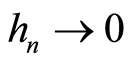 且
且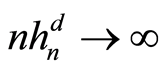 ,则
,则
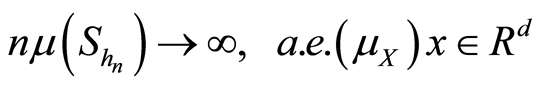 . (3.3)
. (3.3)
引理3([10] ,定理2):设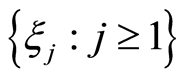 是
是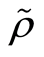 混合的随机序列,
混合的随机序列,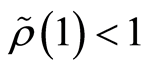 ,
,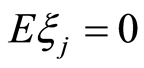 和
和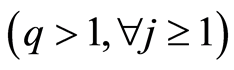
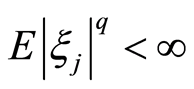 ,则存在与n无关的常数C > 0,使得当
,则存在与n无关的常数C > 0,使得当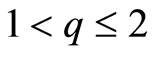 时
时
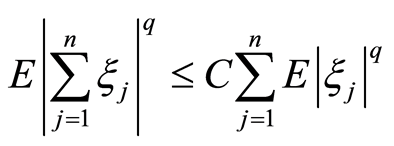 , (3.4)
, (3.4)
当q > 2时
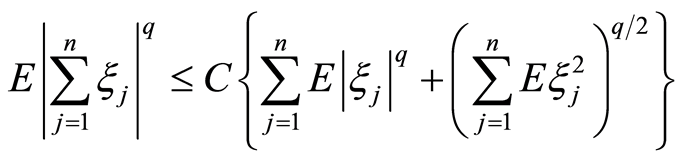 . (3.5)
. (3.5)
引理4:设条件(A1)~(A3)成立。记
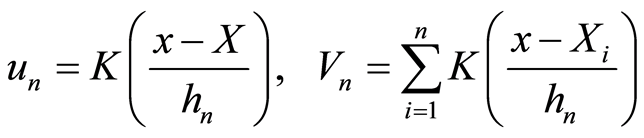 . (3.6)
. (3.6)
则当n充分大时有
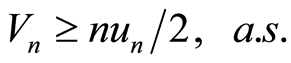 (3.7)
(3.7)
证明:记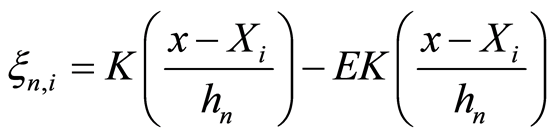 。显然
。显然
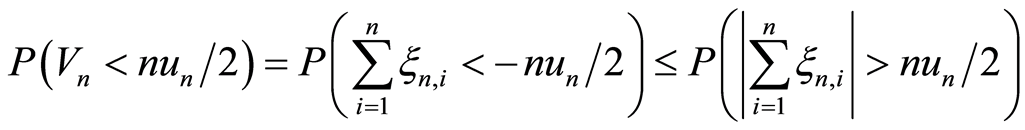 . (3.8)
. (3.8)
对任意实数![]() ,利用条件(A3),有
,利用条件(A3),有 。选择常数
。选择常数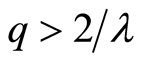 。由于
。由于![]() ,所以
,所以 。根据Markov不等式和引理3,有
。根据Markov不等式和引理3,有
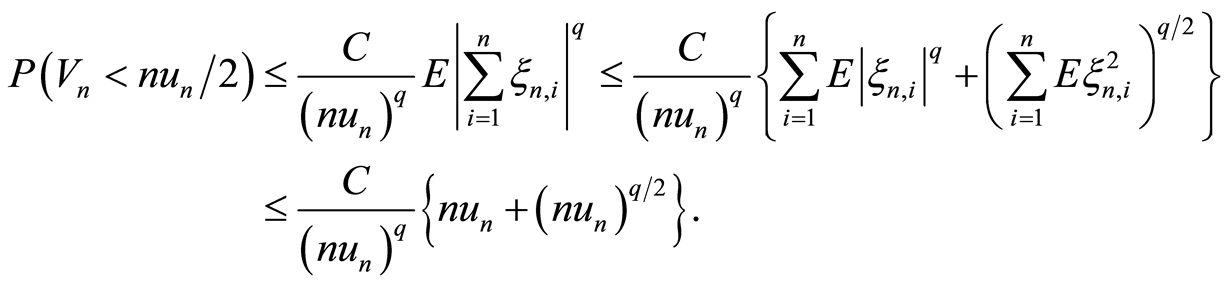 (3.9)
(3.9)
由条件(A3)和引理2知,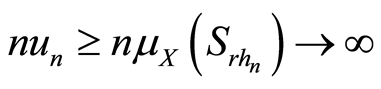 。所以当n充分大时,
。所以当n充分大时,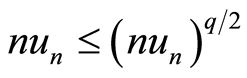 。从而上式变为
。从而上式变为
 . (3.10)
. (3.10)
由于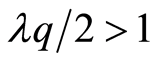 ,所以
,所以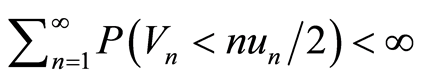 。由Borel-Cantelli引理知,
。由Borel-Cantelli引理知,
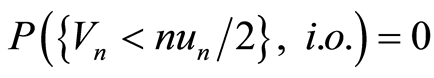 . (3.11)
. (3.11)
因此,存在![]() ,当
,当![]() 时,
时,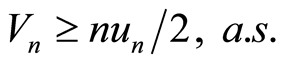 证毕。
证毕。
引理5:设条件(A1)-(A3)成立,且 ,如果
,如果![]() ,那么
,那么
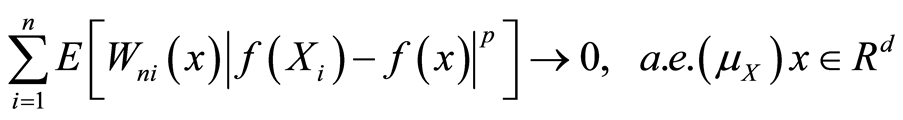 (3.12)
(3.12)
证明:由条件(A3)和引理4知,当n充分大时
 (3.13)
(3.13)
由条件(A3),有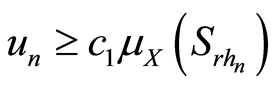 。于是
。于是
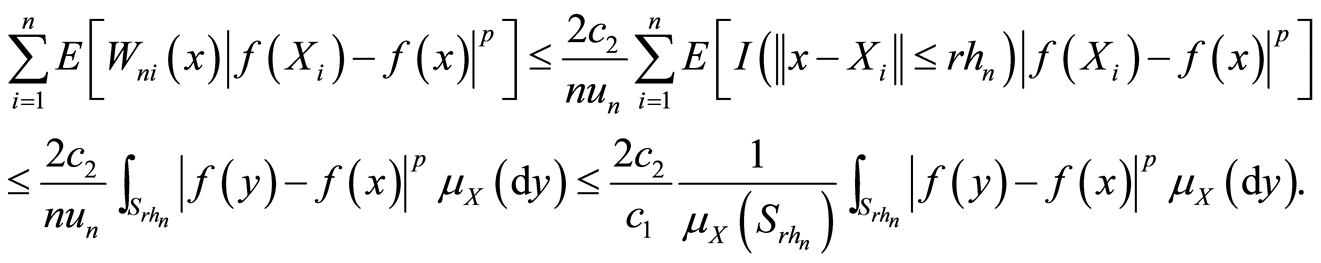 (3.14)
(3.14)
由引理1知,上式趋向于0。证毕。
定理1的证明:记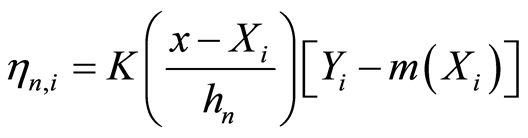 。显然,
。显然,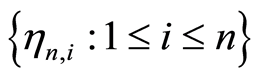 是
是 混合,
混合, 。令
。令
 . (3.15)
. (3.15)
我们有
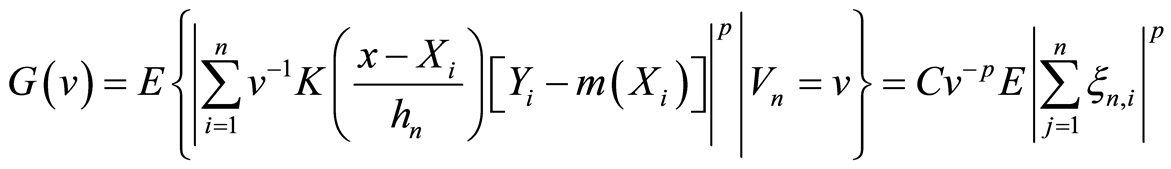 . (3.16)
. (3.16)
当p > 2时,由引理3
 . (3.17)
. (3.17)
令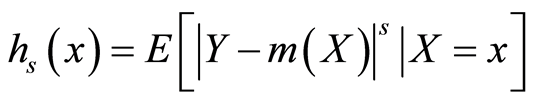 。对任意的常实数
。对任意的常实数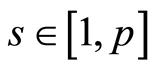 ,有
,有
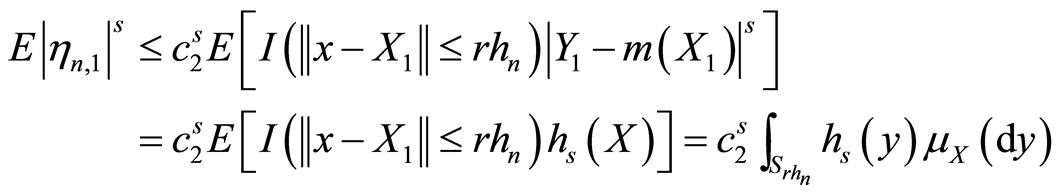 (3.18)
(3.18)
由于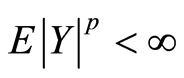 ,所以
,所以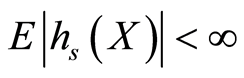 。利用引理1,得
。利用引理1,得 。从而
。从而
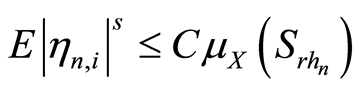 . (3.19)
. (3.19)
将此代入(3.17)式,且注意到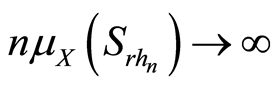 (引理2),得
(引理2),得
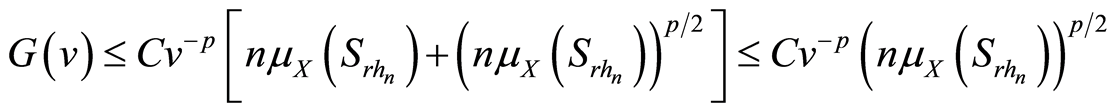 . (3.20)
. (3.20)
由此和引理4,得
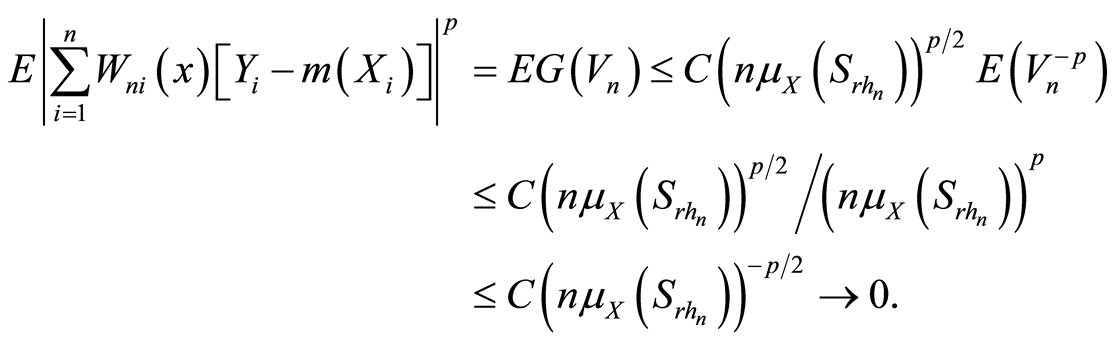 (3.21)
(3.21)
当 时,由(3.16)式和引理3
时,由(3.16)式和引理3
 . (3.22)
. (3.22)
因此
 (3.23)
(3.23)
联合(3.21)式和(3.23)式得结论。证毕。
定理2的证明:令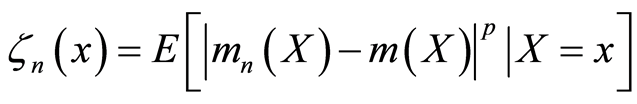 。由定理1知,对x关于概率测度
。由定理1知,对x关于概率测度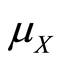 几乎处处有
几乎处处有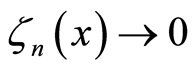 。也就是,
。也就是,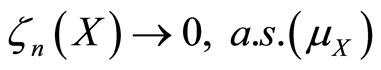 。如果存在可积函数
。如果存在可积函数![]() 满足
满足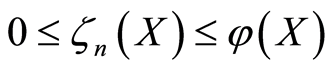 ,则由控制收敛定理得
,则由控制收敛定理得
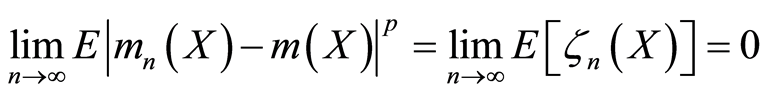 , (3.24)
, (3.24)
这就是定理的结论。所以余下我们只需证明存在这样的可积函数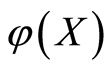 。
。
令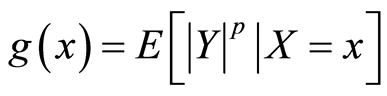 。显然,
。显然, ,且
,且
 (3.25)
(3.25)
利用Holder不等式
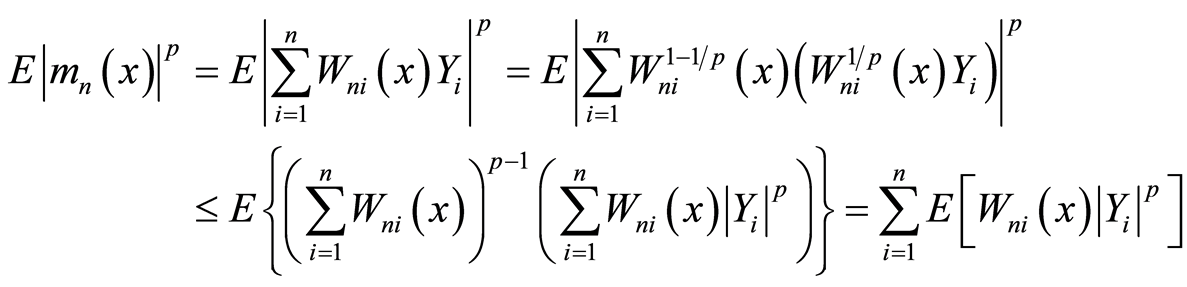 (3.26)
(3.26)
而由条件(A3)和引理4
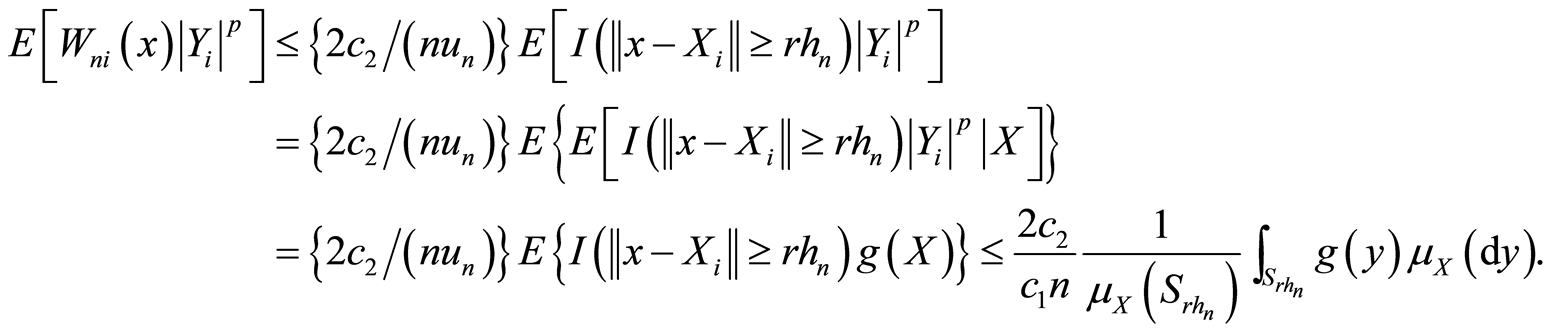 (3.27)
(3.27)
联合上面两式,且利用引理1,有
 . (3.28)
. (3.28)
从而存在正常数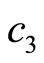 使得
使得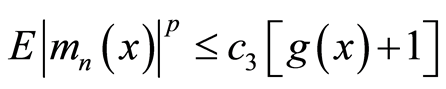 。因此
。因此
 . (3.29)
. (3.29)
令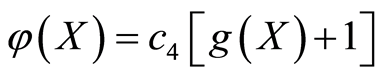 。由于
。由于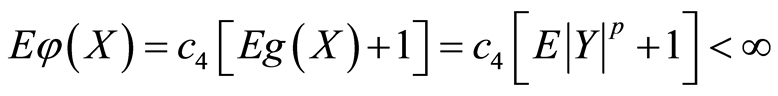 ,所以
,所以![]() 。因此,函数
。因此,函数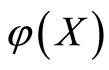 满足要求。证毕。
满足要求。证毕。
基金项目
国家自然科学基金项目(11461009),广西自然科学基金项目(2011GXNSFA018133)。
参考文献 (References)
- [1] Nadaraya, E.A. (1964) On estimating regression. Theory of Probability and Its Applications, 9, 141-142.
- [2] Nadaraya, E.A. (1965) On non-parametric estimates of density functions and regression curves. Theory of Probability and Its Applications, 10, 186-190.
- [3] Watson, G.S. (1964) Smooth regression analysis. Sankhya: The Indian Journal of Statistics, Series A, 26, 359-372.
- [4] Devroye, L. (1981) On the almost everywhere convergence of nonparametric regression function estimates. The Annals of Statistics, 9, 1310-1319.
- [5] Devroye, L.P. and Wagner, T.J. (1980) Distribution-free consistency results in nonparametric discrimination and regression function estimation. The Annals of Statistics, 8, 231-239.
- [6] Greblicki, W., Krzyzak, A. and Pawlak, M. (1984) Distribution-free pointwise consistency of kernel regression estimate. The Annals of Statistics, 12, 1570-1575.
- [7] Nze, P.A., Buhlmann, P. and Doukhan, P. (2002) Weak dependence beyond mixing and asymptotics for nonparametric regression. Annals of Statistics, 30, 397-430.
- [8] Bradley, R.C. (1990) Equivalent mixing conditions for random fields. Technical Report No. 336, Center for Stochastic Processes, University of North Carolina, Chapel Hill.
- [9] Bradley, R.C. (1992) On the spectral density and asymptotic normality of weakly dependent random fields. Journal of Theoretical Probability, 5, 355-374.
- [10] 杨善朝 (1998) 一类随机变量部分和的矩不等式及其应用. 科学通报, 17, 1823-1828.