Pure Mathematics
Vol.06 No.01(2016), Article ID:16790,9
pages
10.12677/PM.2016.61001
An Algorithm of Structural Equation Model with Convergence and Unique Solution
Qian Liu, Shengshuang Chen*, Hengqing Tong
Department of Mathematics, College of Science, Wuhan University of Technology, Wuhan Hubei

Received: Nov. 2nd, 2015; accepted: Jan. 14th, 2016; published: Jan. 20th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The algorithm of structural equation model, partial least squares (PLS), has been widely applied to solve indefinite equations. But the iterative algorithm may have the problem of non-convergent and non-unique. In this paper, we propose an optimized algorithm based on the unit modular length constraint of latent variables and the prescription constraint of path coefficients. Simultaneously, we prove the convergence of the algorithm and take a set of data to validate the uniqueness of the solution.
Keywords:Unit Modular Length Constraint, Prescription Constraint, Convergence, Uniqueness

一种收敛且解唯一的SEM算法
刘倩,陈盛双*,童恒庆
武汉理工大学理学院数学系,湖北 武汉

收稿日期:2015年11月2日;录用日期:2016年1月14日;发布日期:2016年1月20日

摘 要
结构方程模型的PLS算法已广泛应用于求解不定方程组,但这种迭代算法可能存在着不收敛或者解不唯一的问题。本文基于对潜变量进行单位模长约束和对路径系数进行配方约束改进原有算法,由此提出一种收敛且解唯一的优化算法,并证明该算法的收敛性以及利用一组算例对解的唯一性进行说明。
关键词 :单位模长约束,配方约束,收敛性,唯一性

1. 引言
结构方程模型(Structural Equation Modeling, SEM)早期又称做线性结构方程模型或称做工变数结构分析。SEM起源于二十世纪二十年代遗传学家Eswall Wright发明的路径分析,70年代开始应用于心理学、社会学等领域,现在SEM技术已广泛运用到众多学科中。而结构方程模型属于不定方程组,目前求解模型常采用的方法是偏最小二乘法(Partial Least Squares Method, PLS) [1] ,一种新型的多元统计数据分析方法,早在70年代Herman Wold就在经济学研究中引入偏最小二乘法进行路径分析,创建了非线性迭代偏最小二乘算法(Nonlinear Iterative Partial Least Squares Algorithm, NIPALS),至今仍然是PLS中最常用和核心的算法;用最简的方法求得一些绝对不可知的真值,而令误差平方和为最小。PLS方法在近年来快速发展,已有学者在改进和发展方面作出了一些努力,但是我们在计算中还是会遇到不收敛,结果不唯一的情况。本文的工作在于探索结构方程模型,即使本身是不定方程,但可以尝试提出基于潜变量的模长约束和路径系数的配方约束的优化算法,由此克服传统迭代算法的弊端。
本文结构如下:第2部分介绍结构方程模型及其PLS算法;第3部分在对潜变量的模长单位化的条件下,求出PLS的最优迭代初值;第4部分详细证明最优迭代初值下的PLS算法收敛;第5部分基于模长约束的条件下,进一步对模型中的路径系数进行配方约束,使得不定方程求得合理的唯一解。并利用一个算例进行验证。第6部分进行总结。
2. 结构方程模型及其PLS算法
结构方程模型包含两个变量:潜变量(不能直接测量)和观测变量(能直接测量);包含两个方程组:结构方程组(包含潜变量和观测变量)和观测方程组(只包含观测变量)。
图1中的古建筑火灾风险评估模型是一个典型的结构方程模型,有7个潜变量(一级指标),其中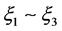 为外生潜变量(自变量),
为外生潜变量(自变量),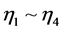 为内生潜变量(因变量);11条路径系数,其中
为内生潜变量(因变量);11条路径系数,其中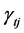 表示自变量到因变量之间的路径关系,见虚线箭头;
表示自变量到因变量之间的路径关系,见虚线箭头;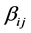 表示因变量之间的路径关系,见实线箭头;
表示因变量之间的路径关系,见实线箭头; (二级指标)为潜变量所带的观测变量。图1中的结构方程表示如下(
(二级指标)为潜变量所带的观测变量。图1中的结构方程表示如下( 是随机误差项):
是随机误差项):
 (1)
(1)
事实上,以上结构方程可以用向量和矩阵来进行一般表示。令 ,
, ,设
,设
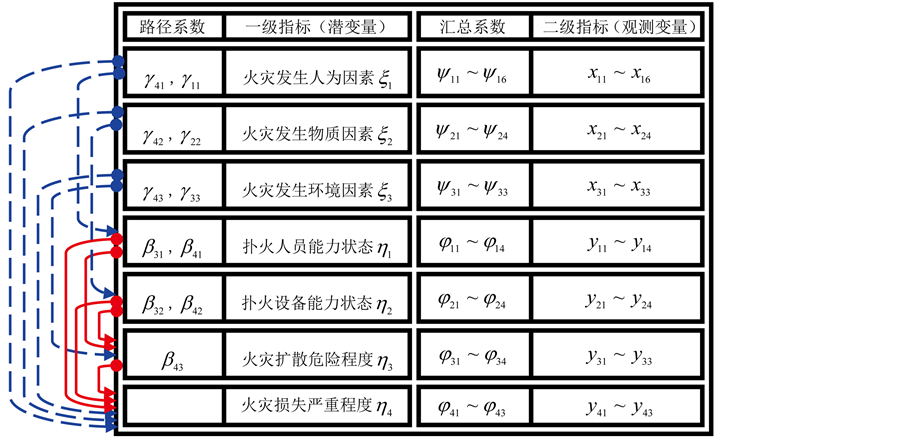
Figure 1. Ancient building fire risk assessment model
图1. 古建筑火灾风险评估模型
 的载荷矩阵为
的载荷矩阵为 ,
, 的载荷矩阵为
的载荷矩阵为 ,残差为
,残差为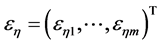 ,则(1)可写成:
,则(1)可写成:
 (2)
(2)
若 中有
中有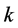 个自变量和
个自变量和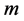 个因变量,
个因变量, 是与
是与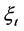 相关的观测变量,
相关的观测变量, ,
, 。
。 是与
是与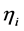 相关的观测变量,
相关的观测变量,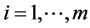 ,
,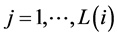 。图1中
。图1中 ,
, ,
, ,
, ,其中
,其中 、
、 表示潜变量所对应的观测变量个数。图1的观测方程可以表示为:
表示潜变量所对应的观测变量个数。图1的观测方程可以表示为:
 ,
, (3)
(3)
 ,
, (4)
(4)
其中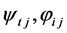 是汇总系数,
是汇总系数, 是随机误差项。
是随机误差项。
记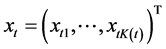 ,
, ,
,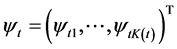 ,
, ,则(3) (4)可表示为:
,则(3) (4)可表示为:
 ,
, (5)
(5)
 ,
,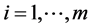 (6)
(6)
从逆向来考虑,观测方程组也可写成:
 ,
,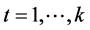 (7)
(7)
 ,
,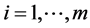 (8)
(8)
记 ,
, ,则观测方程组(7) (8)可表示为:
,则观测方程组(7) (8)可表示为:
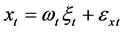 ,
, (9)
(9)
 ,
,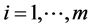 (10)
(10)
把(2) (5) (6) ((2) (9) (10)合称为结构方程模型。
对于求解结构方程模型,目前我们通常采用偏最小二乘法(PLS) [2] -[5] 。PLS迭代法是先对(3) (4)中 赋值,利用给定的
赋值,利用给定的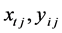 的值,代入(3) (4)得到
的值,代入(3) (4)得到 。这样
。这样 已知,接着求解(2)的最小二乘解,也就是
已知,接着求解(2)的最小二乘解,也就是 ,进一步得到
,进一步得到 。
。 与
与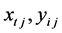 均给定,代入(3) (4),得到
均给定,代入(3) (4),得到 ,就不用再任意赋值。此时,利用所求的
,就不用再任意赋值。此时,利用所求的 ,又可以进行下一轮的迭代。这里迭代收敛是指上述过程中一切元素的差值在限定的误差范围内。上述迭代过程可以表示为:
,又可以进行下一轮的迭代。这里迭代收敛是指上述过程中一切元素的差值在限定的误差范围内。上述迭代过程可以表示为:

在这里,迭代初值是任意赋值,往往导致PLS算法收敛太慢,甚至不收敛,也就是无解。为了克服这个问题,我们需要找到一个合适的迭代初值以确保迭代算法有解。
3. 单位模长约束下的最优迭代初值
以往的PLS方法是对(3) (4)任意给出初值进行,而如果对(7) (8)(或者(9) (10))进行计算,在合理的约束条件下,得到不定方程组的最优代初值是完全可以的[6] [7] 。
下面推导SEM在单位模长约束下的最优迭代初值。对于(7)或(9),假设 与
与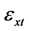 独立,
独立,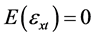 ,此时有
,此时有 ,对(9)右乘
,对(9)右乘 求期望得:
求期望得:
 (11)
(11)
取潜变量为单位向量,即 ,则有
,则有
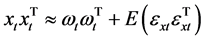 (12)
(12)
显然, 是对角矩阵,且
是对角矩阵,且
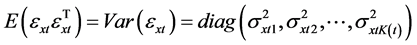 (13)
(13)
(12) (13)联立可得:
 (14)
(14)
取对角线的元素相等,即:
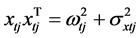 ,
,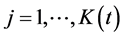 (15)
(15)
我们首先求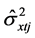 ,令协方差矩阵
,令协方差矩阵 ,则
,则 。进而得到
。进而得到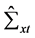 的对角线元素,记为
的对角线元素,记为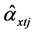 。根据因子分析,得到:
。根据因子分析,得到:
 ,
, (16)
(16)
将(16)代入(15)就有
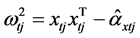 ,
, (17)
(17)
求出了 ,再来估计
,再来估计 。令
。令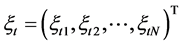 ,在(7)中
,在(7)中 的第
的第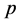 个分量上左乘
个分量上左乘 :
:
 (18)
(18)
令 ,而
,而 中已经包含了
中已经包含了 对
对 的影响,即(18)可写成
的影响,即(18)可写成
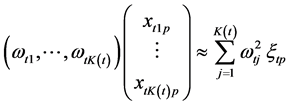 (19)
(19)
 ,
,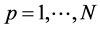 (20)
(20)
这里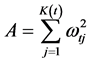 。类似地可以求出
。类似地可以求出 和
和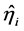 。这样就有了所有潜变量的估计值,它是在单位向量约束下的最小二乘解,也就是偏最小二乘迭代初值,它满足
。这样就有了所有潜变量的估计值,它是在单位向量约束下的最小二乘解,也就是偏最小二乘迭代初值,它满足
 (21)
(21)
上述迭代过程表示为:
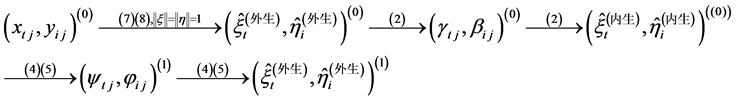
4. 最优迭代初值下的PLS收敛
下面来讨论优化的PLS的收敛性。对(2)变形得:
 (22)
(22)
在建筑火灾风险评估模型中,矩阵 为对角阵且对角线是0,这样
为对角阵且对角线是0,这样 也为对角阵,且
也为对角阵,且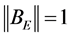 ,即
,即 存在。就有
存在。就有
 (23)
(23)
其中 ,
, 。所以如果
。所以如果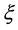 、
、 已知,就可以得到结构方程的最小二乘解。
已知,就可以得到结构方程的最小二乘解。
(23)将(2)的不定方程组转换成一般的回归分析,便于讨论PLS算法的收敛性。但是在这里不能直接利用(23),因为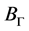 未必能符合路径系数(0元素)的条件。在这里还得根据(1) (2)来考虑PLS的收敛。
未必能符合路径系数(0元素)的条件。在这里还得根据(1) (2)来考虑PLS的收敛。
对于(8)或(10),最优迭代初值 和
和 是在
是在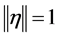 的条件下求出(10)的唯一解。若(23)的解
的条件下求出(10)的唯一解。若(23)的解 先经过单位化再进入(10)迭代,那么其迭代值不变,即迭代收敛。此时已不再是迭代算法,就是一步求出最小二乘解的普通回归分析。
先经过单位化再进入(10)迭代,那么其迭代值不变,即迭代收敛。此时已不再是迭代算法,就是一步求出最小二乘解的普通回归分析。
若(23)的解不经过单位化直接进入(10)迭代,有 。而(23)的第
。而(23)的第 个分量可展开成:
个分量可展开成:
 ,
, (24)
(24)
其最小二乘意义是
 ,
,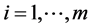 (25)
(25)
将(3) (4)在最小二乘意义下的扩展式代入,此时最小二乘意义是
 (26)
(26)
如果PLS算法不经过(8)而直接进入(4),则系数 无约束,由此我们得到
无约束,由此我们得到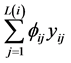 表示由向量
表示由向量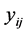 张成的子空间,
张成的子空间, 表示由向量
表示由向量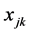 张成的子空间。求两个线性子空间的距离,0解是合理的。而
张成的子空间。求两个线性子空间的距离,0解是合理的。而
最小二乘的本质是向量到子空间的投影,(26)表示两个无约束的子空间的交互投影,此时会无限收敛于0解,因而对任何参数误差控制都能够在这一迭代过程中满足,所以改进的PLS收敛。
5. 配方约束下的优化算法的解唯一
若(7)的一组解为 和
和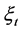 ,显然
,显然 和
和 (
(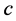 为非0常数)同样是(7)的一组解。说明改变变量的模长不影响方程的解,于是假定
为非0常数)同样是(7)的一组解。说明改变变量的模长不影响方程的解,于是假定 ,就得到单位模长约束的最小二乘解。考虑到不定方程的解不唯一,如果进一步加入合理的约束条件,就能得到方程的唯一解。
,就得到单位模长约束的最小二乘解。考虑到不定方程的解不唯一,如果进一步加入合理的约束条件,就能得到方程的唯一解。
事实上,在求出模长约束最小二乘解后,改变(3)中潜变量的模长,再进行配方约束[8] [9] ,也就是使观测变量到结构变量的汇总系数 非负且其和为1。即:
非负且其和为1。即:
 ,
, ,
, (27)
(27)
具体运算如下:由第3节可知
 ,
,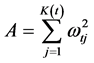 ,
,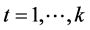 (28)
(28)
对照(3),此时汇总系数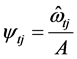 ,此时并不满足配方条件,由于(3)中的潜变量的模长可以任意改变,我们可以在(3)两边同除以
,此时并不满足配方条件,由于(3)中的潜变量的模长可以任意改变,我们可以在(3)两边同除以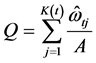 ,则新汇总系数
,则新汇总系数 ,即满足了配方条件。也就求出:
,即满足了配方条件。也就求出:
 ,
, ,
, ,
,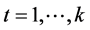 (29)
(29)
类似的,在(4)中求 和
和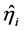 。将
。将 和
和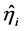 代入(2)就有矩阵
代入(2)就有矩阵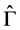 和
和 。以上就求解出
。以上就求解出 的唯一解。
的唯一解。
下面通过一个算例来验证改进算法的唯一性。第2节的建筑火灾风险评估模型,样本行数取为10; 6,4,3,4,4,3,3表示7个潜变量对应的观测变量个数,这样样本列数为27。模型中 是自变量,是基本变量,对其它变量都起作用;因变量为
是自变量,是基本变量,对其它变量都起作用;因变量为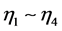 ,其中
,其中 是隐含的效标变量,在本模型中也是汇总的风险评估指标。原始数据如表1。
是隐含的效标变量,在本模型中也是汇总的风险评估指标。原始数据如表1。
从结构方程模型的分析结果不仅可以看到建筑火灾风险中各个隐含变量(潜变量)对应的汇总系数(见表2),而且可以看到各个隐含变量之间的相互影响系数(见表3);例如在古建筑火灾风险评估中,我们可以轻易的找到对各个隐含变量影响最大的观测变量:对火灾发生人为因素影响最大的是第6个问题(0.1743),对火灾发生物质因素影响最大的是第1个问题(0.2700),对火灾发生环境因素影响最大的是第2个问题(0.3445),对扑火人员能力状态影响最大的是第4个问题(0.2612),对扑火设备能力状态影响因素最大的是第3个问题(0.2637),对火灾扩散危险程度影响最大的是第2个问题(0.3480);在隐含变量之间,我们可以看到,扑火设备能力状况对火灾损失严重程度影响相当大(0.8992),其次是火灾发生物质因素(−0.4877)和火灾发生环境因素(0.3828)。同时,采用运用本文提出的优化算法,隐含变量的估计值(见表4)不会出现负值,否则也不符合实际情况。其实我们还可以得到更多更深入的分析成果,有利于我们发现问题,改进工作。
Table 1. Original data
表1. 原始数据
Table 2. Prescription constraint of summary coefficients
表2. 配方约束下的汇总系数
Table 3. Path coefficient of latent variables
表3. 潜变量的路径系数
Table 4. Estimates of latent variables
表4. 潜变量的估计值
6. 总结
本文主要提出了一种收敛且解唯一的算法。首先,在潜变量为单位模长的条件下,求出 的模长约束最小二乘解,也是PLS的最优迭代初值,由此使PLS算法收敛。另外,在模长约束最小二乘解的基础上进一步改变其模长,使观测方程组的汇总系数满足配方约束(所有汇总系数非负且其和为1),进而对结构方程组直接求解,从而得到
的模长约束最小二乘解,也是PLS的最优迭代初值,由此使PLS算法收敛。另外,在模长约束最小二乘解的基础上进一步改变其模长,使观测方程组的汇总系数满足配方约束(所有汇总系数非负且其和为1),进而对结构方程组直接求解,从而得到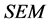 的唯一解。本文的优化算法,优点在于回避了传统迭代算法不收敛和不唯一的问题,大大提高计算的收敛速度,同时确保计算的唯一性。
的唯一解。本文的优化算法,优点在于回避了传统迭代算法不收敛和不唯一的问题,大大提高计算的收敛速度,同时确保计算的唯一性。
基金项目
国家“863”高技术研究发展计划基金资助项目(20121g0139)。
文章引用
刘 倩,陈盛双,童恒庆. 一种收敛且解唯一的SEM算法
An Algorithm of Structural Equation Model with Convergence and Unique Solution[J]. 理论数学, 2016, 06(01): 1-9. http://dx.doi.org/10.12677/PM.2016.61001
参考文献 (References)
- 1. Fornell, C. and Bookstein, F.L. (1982) Two Structural Equation Models: LISREL and PLS Applied to Consumer Ex-it-Voice Theory. Journal of Marketing Research, 19, 440-452. http://dx.doi.org/10.2307/3151718
- 2. 王惠文. 偏最小二乘回归方法及其应用[M]. 北京: 国防工业出版社, 1999.
- 3. 王惠文, 刘强. 偏最小二乘回归模型内涵分析方法研究[J]. 北京航空航天大学学报, 2000, 26(4): 473-476.
- 4. 罗批, 郭继昌, 李锵, 滕建辅. 基于偏最小二乘回归建模的探讨[J]. 天津大学学报, 2002, 35(6): 783-786.
- 5. Tong, H.Q. (1993) Evaluation Model and Its It-erative Algorithm by Alternating Protecting. Mathematical and Computer Modelling, 18, 55-60. http://dx.doi.org/10.1016/0895-7177(93)90162-R
- 6. Tong, Q.L., Zou, X.C., Wang, C.M. and Tong, H.Q. (2010) A Definite Linear Algorithm for Structural Equation Model. Mathematical and Computer Modelling, 52, 744-751. http://dx.doi.org/10.1016/j.mcm.2010.05.002
- 7. Wang, C.M. and Tong, H.Q. (2007) Best Iterative Initial Values for PLS in a CSI Model. Mathematical and Computer Modelling, 46, 439-444. http://dx.doi.org/10.1016/j.mcm.2006.10.009
- 8. 董汉忠, 张小薇. 配方回归[J]. 计算机应用通讯, 1983(4): 36-42.
- 9. 方开泰, 王东谦, 吴国富. 一类带约束的回归——配方回归[J]. 计算数学, 1982(1): 57-69.
*通讯作者。
