Pure Mathematics
Vol.06 No.03(2016), Article ID:17354,7
pages
10.12677/PM.2016.63019
Unboundedness of Solutions of Duffing Equations with Damping Term
Tiantian Chen, Peiwen Zhang, Chunrui Han
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong
Received: Apr. 1st, 2016; accepted: Apr. 11th, 2016; published: Apr. 14th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this article, we prove the unboundedness of solutions for the Duffing equations with damping term  and
and 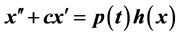 under some easier testing conditions.
under some easier testing conditions.
Keywords:Unbounded Solutions, Duffing Equations, Damping Term

带阻尼项的Duffing方程解的无界性
陈甜甜,张沛文,韩春瑞
中国海洋大学数学科学学院,山东 青岛
收稿日期:2016年4月1日;录用日期:2016年4月11日;发布日期:2016年4月14日

摘 要
在比较容易验证的条件下,本文证明了带有阻尼项的Duffing方程 和
和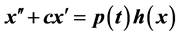 的所有解都是无界的。
的所有解都是无界的。
关键词 :无界解,Duffing方程,阻尼项

1. 引言
1996年,Alonso和Ortega [1] 研究了共振点处Duffing方程 的无界解的存在性问题。在
的无界解的存在性问题。在 和
和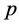 满足
满足 的条件下,证明了该方程的所有解都是无界的。这里的无界性指的是满足
的条件下,证明了该方程的所有解都是无界的。这里的无界性指的是满足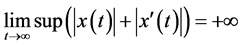 。我们知道共振常常导致有无界解 [2] [3] 。带有阻尼的常
。我们知道共振常常导致有无界解 [2] [3] 。带有阻尼的常
系数线性方程由于能量的耗散,在周期强迫力的作用下所有解是有界的 [3] 。很自然的问题是,带有阻尼项的非线性方程是否有无界解。本文的目的就是在比较容易验证的条件下证明带有阻尼的Duffing方程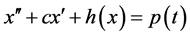 和
和 的所有解都是无界的。
的所有解都是无界的。
2. 关于差分方程的一个抽象结果
设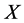 是一个Banach空间。在
是一个Banach空间。在 中考虑差分方程:
中考虑差分方程:
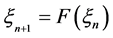 , (1)
, (1)
其中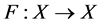 是一个算子。定义
是一个算子。定义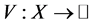 ,
, 是实数集,并且满足:
是实数集,并且满足:
 。 (2)
。 (2)
Alonso和Ortega [1] 证明了如下引理:
引理2.1 设存在函数 满足(2)式,并且存在正常数
满足(2)式,并且存在正常数 和
和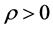 满足:
满足:
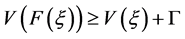 ,当
,当 。 (3)
。 (3)
设 并且满足
并且满足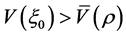 ,则差分方程(1)满足初始条件为
,则差分方程(1)满足初始条件为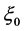 的解满足:
的解满足:
 。
。
推论2.2 设 是有限维的且
是有限维的且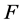 是连续的。如果存在一个连续的函数
是连续的。如果存在一个连续的函数 满足:
满足:
 (4)
(4)
则差分方程(1)的所有解都满足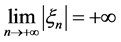 。
。
3. 解的无界性
我们主要讨论以下两种方程:
 (5)
(5)
和
 (6)
(6)
的无界解的存在性问题。其中,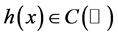 ,
, ,
,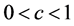 。
。
引理3.1 存在常数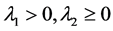 ,使得方程(5)、(6)的解均满足:
,使得方程(5)、(6)的解均满足:
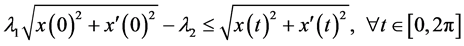 。
。
证明:我们只对方程(5)给出证明,对方程(6)同理可证。考虑辅助方程
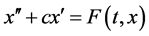 , (7)
, (7)
其中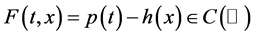 。令
。令 ,则
,则 。于是
。于是
 (8)
(8)
其对应的齐次方程组为
 。 (9)
。 (9)
由

可得,方程(9)系数矩阵的特征根为: 。
。
求得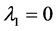 对应的特征向量为
对应的特征向量为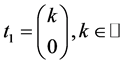 ,
,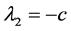 对应的特征向量为
对应的特征向量为 。于是方程(9)的通解为:
。于是方程(9)的通解为:
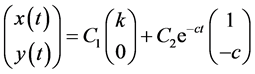 。
。
所以,方程(9)的基解矩阵为:
 。
。
容易计算
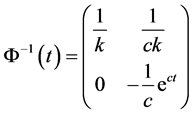 。
。
根据 [4] 中的结果可知,若方程组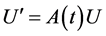 的一个基解矩阵为
的一个基解矩阵为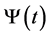 ,则初值问题
,则初值问题

与积分方程组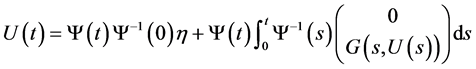 等价。所以方程组(8)的
等价。所以方程组(8)的
解可以表示为:
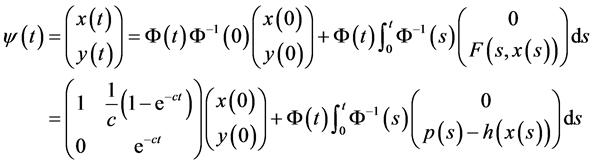 。
。
记
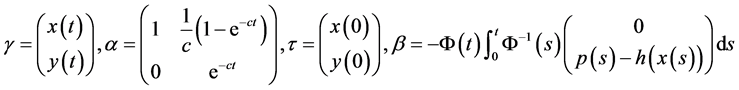 ,
,
则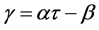 。
。
由三角不等式可得, 。其中,
。其中,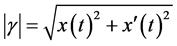 ,而
,而
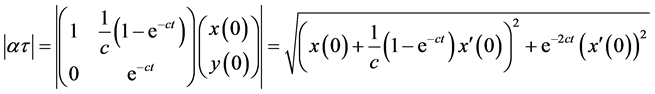 。
。
记
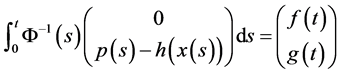 ,
,
则
 。
。
1) 当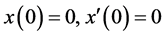 时,
时,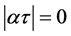 ,令
,令 ,则对
,则对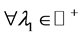 ,有
,有
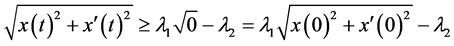 ,所以结论成立。
,所以结论成立。
2) 当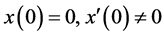 时,
时,
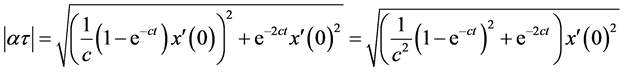 。
。
令 ,
, ,则有
,则有
 ,所以结论成立。
,所以结论成立。
3) 当 但
但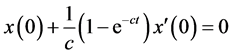 时,即
时,即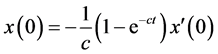 。
。
此时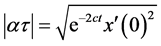 ,所以总会存在
,所以总会存在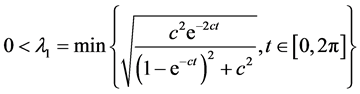 ,使得
,使得
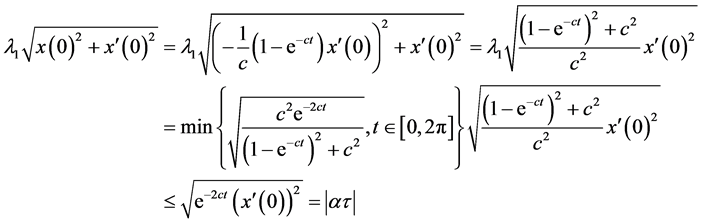 。
。
令 ,则有,
,则有,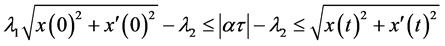 ,
,
所以结论成立。
4) 当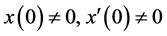 且
且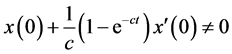 时,对
时,对 ,有
,有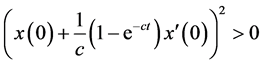 ,所以一定存在
,所以一定存在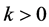 ,使得
,使得
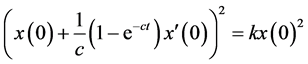 。
。
令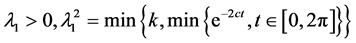 ,
,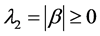 则
则
 。
。
由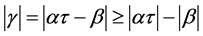 得,
得,
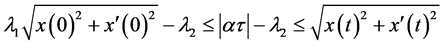 ,
,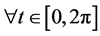 。
。
综上所述,存在常数 ,使得方程(5)的解满足:
,使得方程(5)的解满足:
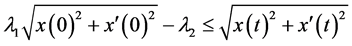 ,
,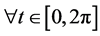 。
。
定理3.2 设 有上界、非常数,且
有上界、非常数,且 ,则方程(5)的所有
,则方程(5)的所有
解都是无界的,即满足:
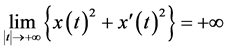 。 (10)
。 (10)
证明:给定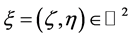 ,用
,用 表示方程(5)的解,并设初始条件为:
表示方程(5)的解,并设初始条件为: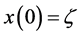 ,
,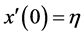 。
。
我们用抽象的形式定义: 。根据引理3.1,为了证明(10)式,我们只需要证明由差分方程
。根据引理3.1,为了证明(10)式,我们只需要证明由差分方程 ,
,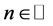 给出的序列
给出的序列 及任意给定的初值
及任意给定的初值 满足
满足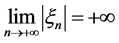 即可。我们仅考虑
即可。我们仅考虑 的情形,
的情形, 可由代换
可由代换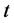 为
为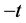 得到。
得到。
定义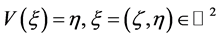 。由分部积分公式可得
。由分部积分公式可得
 。
。
所以,
 。
。
因此由推论2.2得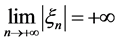 ,进而可得方程(5)解的无界性,即方程(5)的解满足:
,进而可得方程(5)解的无界性,即方程(5)的解满足: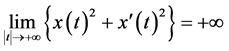 。
。
举例1 考虑摆型方程
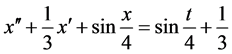 。 (11)
。 (11)
因为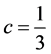 ,
,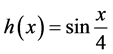 ,
,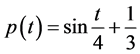 ,因此
,因此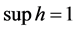 。而
。而
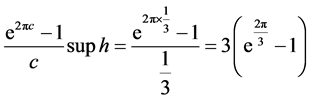 ,
,
 。
。
满足定理3.2的条件,因此方程(11)的所有解无界。另一方面,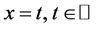 显然是方程的一个无界解。
显然是方程的一个无界解。
定理3.3 设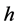 有下界、非常数,且
有下界、非常数,且 ,则方程(6)的所有解都是无界解,即满足:
,则方程(6)的所有解都是无界解,即满足: 。
。
证明:由定理3.2的证明可知,
 。
。
所以,由推论2.2得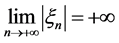 ,进而可得方程(6)解的无界性,即方程(6)的解满足:
,进而可得方程(6)解的无界性,即方程(6)的解满足:
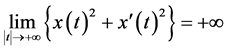 。
。
举例2 考虑方程
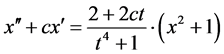 。 (12)
。 (12)
由于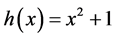 ,所以
,所以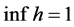 。而
。而 有
有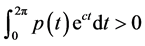 ,所以
,所以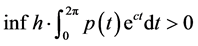 。满足定理3.3的条件,因此方程(12)的所有解无界。另一方面,
。满足定理3.3的条件,因此方程(12)的所有解无界。另一方面,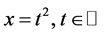 显然是方程的一个无界解。
显然是方程的一个无界解。
致谢
本文作者对朴大雄教授的指导表示感谢。
基金项目
本文得到国家级大学生创新创业训练计划项目(201510423116)和山东省自然科学基金(ZR2013AM026)的资助。
文章引用
陈甜甜,张沛文,韩春瑞. 带阻尼项的Duffing方程解的无界性
Unboundedness of Solutions of Duffing Equations with Damping Term[J]. 理论数学, 2016, 06(03): 127-133. http://dx.doi.org/10.12677/PM.2016.63019
参考文献 (References)
- 1. Alonso, J. and Ortega, R. (1996) Unbounded Solutions of Semilinear Equations at Resonance. Nonlinearity, 9, 1099- 1111. http://dx.doi.org/10.1088/0951-7715/9/5/003
- 2. 张芷芬, 等. 微分方程定性理论[M]. 北京: 科学出版社, 1997: 435-436.
- 3. Ding, T. (1982) Nonlinear Oscillations at a Point of Resonance. Scientia Sinica, 25, 918-931.
- 4. 王高雄, 等. 常微分方程[M]. 第3版. 北京: 高等教育出版社, 2006: 219.