Pure Mathematics
Vol.07 No.03(2017), Article ID:20482,4
pages
10.12677/PM.2017.73016
Periodicity of a Class of Functional Equations
Xiaoli Zhou1, Tiejun Zhou1,2
1College of Science, Hunan Agricultural University, Changsha Hunan
2College of Orient Science and Technology, Hunan Agricultural University, Changsha Hunan

Received: Apr. 22nd, 2017; accepted: May 6th, 2017; published: May 10th, 2017

ABSTRACT
The sufficient conditions are obtained that the 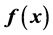 is a periodic function with period 2T, 3T or 4T for the functional equation
is a periodic function with period 2T, 3T or 4T for the functional equation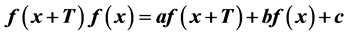 . The results generalize the existing conclusions.
. The results generalize the existing conclusions.
Keywords:Functional Equation, Period

一类函数方程的周期性
周小利1,周铁军1,2
1湖南农业大学理学院,湖南 长沙
2湖南农业大学东方科技学院,湖南 长沙

收稿日期:2017年4月22日;录用日期:2017年5月6日;发布日期:2017年5月10日

摘 要
本文针对函数方程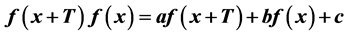 分别获得
分别获得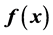 是周期为2T、3T、4T函数的充分条件,推广了已有结论。
是周期为2T、3T、4T函数的充分条件,推广了已有结论。
关键词 :函数方程,周期

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对于函数方程的解,我们经常要讨论它的周期性,并确定它的周期 [1] [2] [3] [4] [5] 。文献 [1] 中讨论了8种特殊形式的函数方程并给出了它们的周期。本文将该文相关结果推广到如下一般形式的函数方程:
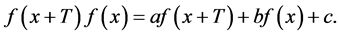 (1)
(1)
显然,当 时,方程(1)存在平凡周期解:
时,方程(1)存在平凡周期解:
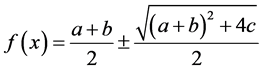
不难验证,当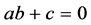 时,方程(1)有常数解
时,方程(1)有常数解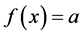 或
或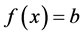 ,这是平凡周期解。那么对于
,这是平凡周期解。那么对于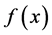 不为常数的情形,方程(1)是否存在周期解?如果存在周期解,它的周期是多少?这是本文要解决的问题。
不为常数的情形,方程(1)是否存在周期解?如果存在周期解,它的周期是多少?这是本文要解决的问题。
2. 主要定理
对于方程(1)是否存在非常数周期解的问题,我们有如下结论:
定理 设f(x)不为常数,
(i) 如果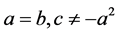 ,那么
,那么 是周期为2T的函数。
是周期为2T的函数。
(ii) 如果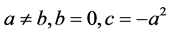 ,那么
,那么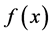 是周期为3T的函数。
是周期为3T的函数。
(iii) 如果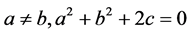 ,那么
,那么 是周期为4T的函数。
是周期为4T的函数。
证明:由于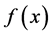 不为常数,则由(1)式可得:
不为常数,则由(1)式可得:
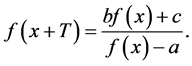 (2)
(2)
于是有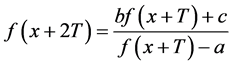 。将(2)式代入并整理得:
。将(2)式代入并整理得:
 (3)
(3)
(i) 如果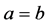 ,则由(3)式可得
,则由(3)式可得 ,即
,即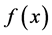 是周期为2T的函数。
是周期为2T的函数。
(ii) 由(2)式得
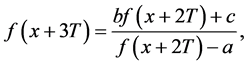
将(3)式代入上式并整理得
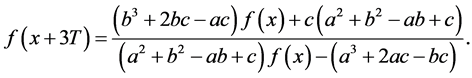 (4)
(4)
如果 ,那么有
,那么有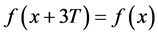 ,即
,即 是周期为3T的函数。
是周期为3T的函数。
(iii) 由(3)式得
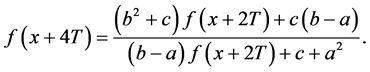
再将(3)式代入上式并整理得
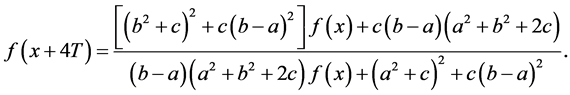
当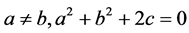 时,有
时,有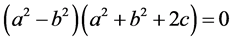 ,于是得
,于是得
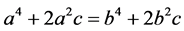
从而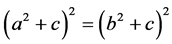 ,故有
,故有
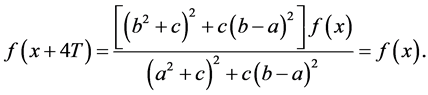
所以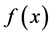 是周期为4T的函数。
是周期为4T的函数。
3. 几个实例
下面举例说明上述定理的应用。
例1. 若函数 满足
满足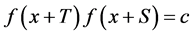 ,其中
,其中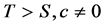 ,则
,则 是周期为
是周期为 的函数(文献 [3] 定理3)。
的函数(文献 [3] 定理3)。
证明:令 ,则有
,则有 ,对应方程(1)中,
,对应方程(1)中,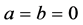 ,
,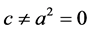 ,故由定理中(i)知,
,故由定理中(i)知,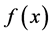 是周期为
是周期为 的函数。
的函数。
注:文献 [1] 中第7点结论是本例在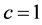 时的特殊情形,文献 [2] 中定理1的两个方程是本例在
时的特殊情形,文献 [2] 中定理1的两个方程是本例在 时的情形。
时的情形。
例2. 若函数 满足
满足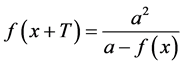 ,则
,则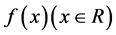 是以3T为周期的函数。
是以3T为周期的函数。
证明:由条件可得
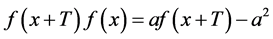 ,
,
因此在方程(1)中,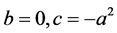 ,由定理中(ii)知道,
,由定理中(ii)知道,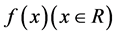 是以3T为周期的函数。
是以3T为周期的函数。
注:若a = 1,则得到文献 [1] 中第8点结论。
例3. 若函数 满足
满足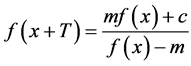 ,则
,则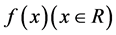 是以2T为周期的函数。
是以2T为周期的函数。
证明:由条件可得
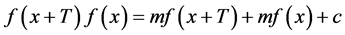
因此在方程(1)中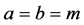 ,由定理1中(i)知道,
,由定理1中(i)知道,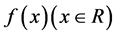 是以2T为周期的函数。
是以2T为周期的函数。
注:若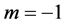 ,
, ,则得到文献 [1] 中第9点结论及文献 [2] 定理2的推论;若
,则得到文献 [1] 中第9点结论及文献 [2] 定理2的推论;若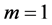 ,
,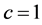 ,则得到文献 [1] 中第11点结论及文献 [2] 中的定理2。
,则得到文献 [1] 中第11点结论及文献 [2] 中的定理2。
例4. 若函数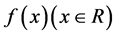 满足
满足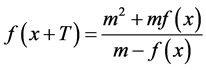 ,则
,则 是以4T为周期的函数。
是以4T为周期的函数。
证明:由条件可得
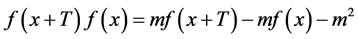 ,
,
因此在方程(1)中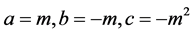 ,显然
,显然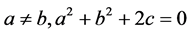 ,故由定理1中(iii)知道,
,故由定理1中(iii)知道,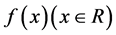 是以4T 为周期的函数。
是以4T 为周期的函数。
注:如果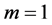 ,就得到文献 [1] 中第10点结论及文献 [2] 中定理3的推论;如果
,就得到文献 [1] 中第10点结论及文献 [2] 中定理3的推论;如果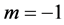 ,就得到文献 [2] 中定理3的结论。
,就得到文献 [2] 中定理3的结论。
4. 结论
我们的研究表明,抽象函数方程(1)除了在系数满足条件 或
或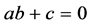 时存在常数形式的平凡周期解外,还可能在不同条件下分别存在周期为2T、3T和4T的非常数的周期解。
时存在常数形式的平凡周期解外,还可能在不同条件下分别存在周期为2T、3T和4T的非常数的周期解。
文章引用
周小利,周铁军. 一类函数方程的周期性
Periodicity of a Class of Functional Equations[J]. 理论数学, 2017, 07(03): 137-140. http://dx.doi.org/10.12677/PM.2017.73016
参考文献 (References)
- 1. 陈维华, 强海萍. 抽象函数的周期性研究[J]. 中学数学杂志, 2011(5): 41.
- 2. 周继军. 由一类函数方程确定的周期函数[J]. 数学教学通讯, 1991(5): 19-20.
- 3. 王良成. 也谈由函数方程确定的周期函数[J]. 数学教学通讯. 1992(5): 14-15.
- 4. 宋泽熙, 周铁军. 一类函数方程周期解周期的确定[J]. 大学数学, 2016(6): 87-90.
- 5. Mickens, R.E. (2016) Periodic Solutions of the Functional Equation . Journal of Difference Equations and Applications, 22, 67-74. https://doi.org/10.1080/10236198.2015.1075520