Pure Mathematics
Vol.07 No.04(2017), Article ID:21066,12
pages
10.12677/PM.2017.74027
The Existence of Solutions for a Class of Boundary Value Problem of Fractional Differential Equations on an Infinite Interval
Jiaxin Yao, Wenxia Wang, Jianmei Jia
Department of Mathematics, Taiyuan Normal University, Jinzhong Shanxi
Received: Jun. 3rd, 2017; accepted: Jun. 19th, 2017; published: Jun. 22nd, 2017

ABSTRACT
By using the Leray-Schauder nonlinear alternative theorem and the Leggett-Williams fixed point theorem, a class of boundary value problem for fractional differential equations with integral conditions on an infinite interval is investigated. Some sufficient conditions on the existence of at least one unbounded solution and three positive solutions are established. At last, two examples are given to illustrate the results.
Keywords:Fractional Differential Equations, Integral Boundary Conditions, Infinite Interval, Positive Solutions
一类无穷区间上的分数阶微分方程边值问题解的存在性
姚佳欣,王文霞,贾建梅
太原师范学院数学系,山西省 晋中
收稿日期:2017年6月3日;录用日期:2017年6月19日;发布日期:2017年6月22日

摘 要
利用Leray-Schauder非线性抉择定理以及Leggett-Williams不动点定理研究了一类无穷区间上的分数阶微分方程积分边值问题,获得了该边值问题至少存在一个无界解和三个正解的充分条件。最后给出了两个例子作为所获结果的应用。
关键词 :分数阶微分方程,积分边值问题,无穷区间,正解

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,由于分数阶微分方程在诸如物理、化学、生物科学和经济学等众多学科领域中的重要应用,其解的存在性问题也受到了众多学者的广泛关注。目前,有限区间上的分数阶微分方程边值问题已获得广泛而深入的研究,并取得了丰富而深刻的结论,参见文献 [1] [2] [3] [4] 。但是,和有限区间相比,无穷区间上的非线性分数阶微分方程的研究还很薄弱。事实上,在研究椭圆方程径向对称解,火箭推进固体燃料静电测量问题,不稳定气流流速等问题时都会产生无穷区间上的边值问题。因此,无穷区间上的分数阶微分方程边值问题的研究具有十分重要的理论与实际意义。最近,一些作者研究了这类问题,获得了一些很有价值的结果,参见文献 [5] - [11] 。其中,在文献 [5] 中,作者研究了如下无穷区间上的非线性分数阶微分方程边值问题:
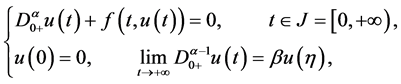 (1.1)
(1.1)
其中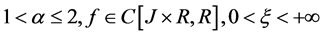 ,
, 是标准的Riemann-Liouville分数阶微分,作者运用Leray- Schauder非线性抉择定理获得了上述方程存在无界解的充分条件。
是标准的Riemann-Liouville分数阶微分,作者运用Leray- Schauder非线性抉择定理获得了上述方程存在无界解的充分条件。
文献 [6] 研究了下列分数阶微分方程在无穷区间上正解的存在唯一性:
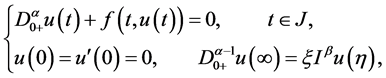 (1.2)
(1.2)
其中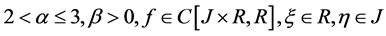 ,
,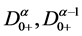 是标准的Riemann-Liouville分数阶微分,
是标准的Riemann-Liouville分数阶微分, 是标准的Riemann-Liouville分数阶积分。作者运用迭代技术获得了上述了边值问题存在唯一解的充分条件。但是文献 [6] 并未讨论方程(1.2)多重正解的存在性。受上述文献启发,本文讨论如下无穷区间上分数阶微分方程边值问题:
是标准的Riemann-Liouville分数阶积分。作者运用迭代技术获得了上述了边值问题存在唯一解的充分条件。但是文献 [6] 并未讨论方程(1.2)多重正解的存在性。受上述文献启发,本文讨论如下无穷区间上分数阶微分方程边值问题:
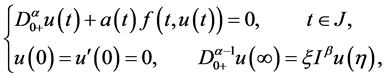 (1.3)
(1.3)
其中 ,
, 是标准的Riemann-Liouville分数阶微分,
是标准的Riemann-Liouville分数阶微分, 是标准的Riemann-Liouville分数阶积分。可以看到,边值问题(1.2)是本文所讨论的边值问题(1.3)的特例。此外,不同于文献 [6] ,本文将使用Leray-Schauder非线性抉择定理以及Leggett-Williams不动点定理,研究边值问题(1.3)的无界解及三重正解存在的充分条件。据我们所知,现有文献尚未对该问题进行研究,因此本文所获结论是新的。
是标准的Riemann-Liouville分数阶积分。可以看到,边值问题(1.2)是本文所讨论的边值问题(1.3)的特例。此外,不同于文献 [6] ,本文将使用Leray-Schauder非线性抉择定理以及Leggett-Williams不动点定理,研究边值问题(1.3)的无界解及三重正解存在的充分条件。据我们所知,现有文献尚未对该问题进行研究,因此本文所获结论是新的。
2. 相关定义和引理
为了方便读者,我们首先给出分数阶微积分的一些基本的定义和引理。
定义2.1 [1] 连续函数 的
的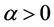 阶Riemann-Liouville分数积分定义为
阶Riemann-Liouville分数积分定义为

其中,等式的右端在 有定义。
有定义。
定义2.2 [1] 连续函数 的
的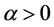 阶Riemann-Liouville分数导数定义为
阶Riemann-Liouville分数导数定义为

其中,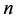 是大于等于
是大于等于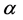 的最小整数,等式的右端在
的最小整数,等式的右端在 有定义。
有定义。
引理2.1 [1] 设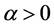 ,如果
,如果 ,则分数阶微分方程
,则分数阶微分方程
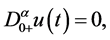
有唯一解:
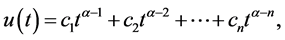
其中 。
。
引理2.2 [1] 如果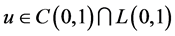 有
有 阶导数属于
阶导数属于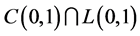 ,则
,则

其中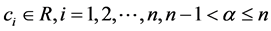 。
。
定理2.1 [1] (Leray-Schauder非线性抉择定理)假设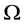 是线性赋范空间
是线性赋范空间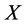 中包含原点的有界开集,
中包含原点的有界开集, 全连续,并且满足边界条件,即当
全连续,并且满足边界条件,即当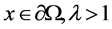 时,
时, ,则
,则 在
在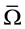 上至少有一个不动点。
上至少有一个不动点。
设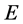 为Banach空间,
为Banach空间, 为
为 中的锥,称映射
中的锥,称映射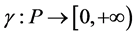 为锥
为锥 上的一个连续凹泛函,如果
上的一个连续凹泛函,如果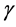 是连续的且对于任意的
是连续的且对于任意的 ,
,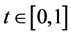 ,
,

对于 和锥
和锥 上的连续凹泛函
上的连续凹泛函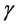 ,定义凸集
,定义凸集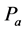 和
和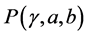 如下:
如下:
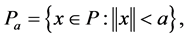

定理2.2 [1] (Leggett-Williams不动点定理)设 是全连续算子,
是全连续算子,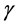 为
为 上的非负连续凹泛函且对于任意的
上的非负连续凹泛函且对于任意的 ,
,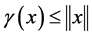 。假定存在
。假定存在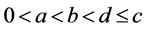 使得
使得
(C1)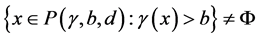 且对于任意的
且对于任意的 ,
,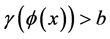 ;
;
(C2) 对任意的 ,有
,有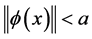 ;
;
(C3) 对任意的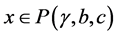 且
且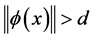 ,有
,有 。
。
则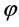 在
在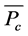 中至少存在三个不动点
中至少存在三个不动点 且满足
且满足

3. 无界解的存在性
考虑下面的齐次边值问题:
 (3.1)
(3.1)
引理3.1 [6] 对于任意的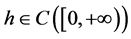 ,
,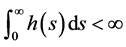 ,如果
,如果 ,则边值问题(3.1)有唯一解
,则边值问题(3.1)有唯一解 ,并且
,并且
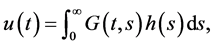
其中Green函数:
 (3.2)
(3.2)
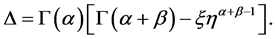
由文献 [6] 我们可以知道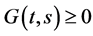 ,
,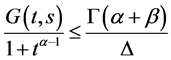 。下面我们给出
。下面我们给出 一些其它的性质:
一些其它的性质:
引理3.2由(3.2)式表示的Green函数 有如下性质:
有如下性质:
1) 对任意的 ,
, 关于
关于 是严格递增的;
是严格递增的;
2) 设实数 ,存在正实数
,存在正实数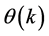 ,使得对
,使得对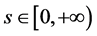

证明:通过对Green函数求导易证得性质1),下面我们主要来证性质2)。令

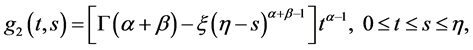
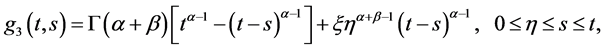

则
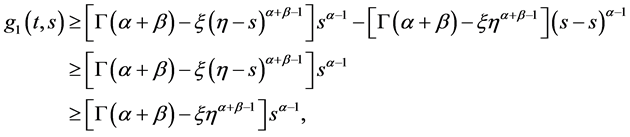


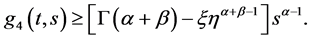
综上
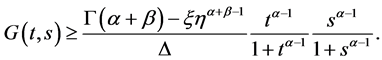
又

即

所以
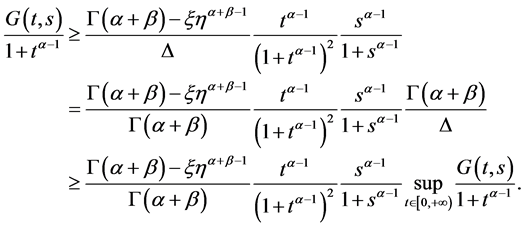
且
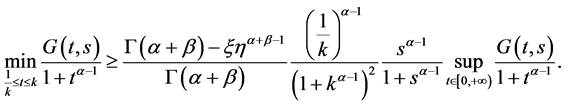
令

则

证毕。
定义空间 为
为
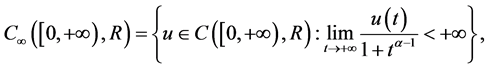
赋予范数

定义锥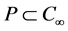 为
为
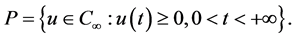
引理3.3 [7] 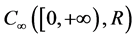 是一个Banach空间。
是一个Banach空间。
本文使用如下条件:
(H1)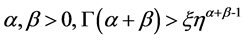 ;
;
(H2) 是连续函数,
是连续函数, ;
;
(H3) 存在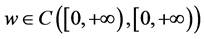 非减,
非减, 使得
使得

定义算子 为:
为:
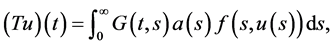 ,
,
易知这样定义的算子是有意义的。根据引理2.1,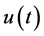 是方程(1.3)的解当且仅当
是方程(1.3)的解当且仅当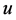 是算子
是算子 的不动点。
的不动点。
引理3.4 [7] 设 为有界集,
为有界集, ,则
,则 是
是 的相对紧集,如果以下
的相对紧集,如果以下
条件成立:
1) 在
在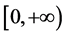 上局部等度连续;
上局部等度连续;
2) 在
在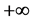 处等度收敛,即对任意的
处等度收敛,即对任意的 ,存在
,存在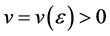 使得对任意的
使得对任意的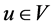 ,
,
成立
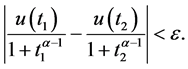
引理3.5如果(H1)~(H3)成立,则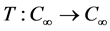 全连续。
全连续。
证明:首先,证明 是连续的。
是连续的。
在空间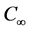 中任取一收敛序列
中任取一收敛序列 。则存在常数
。则存在常数 使得
使得
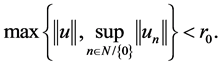
于是

又因为
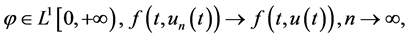
且
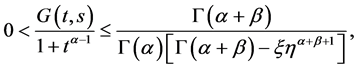
因此,由勒贝格控制收敛定理,结合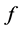 的连续性可得
的连续性可得

所以,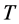 是连续的。
是连续的。
再来证明算子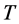 把
把 中的有界集映成列紧集。
中的有界集映成列紧集。
设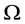 为
为 的有界子集,下证
的有界子集,下证 是一个列紧集。由
是一个列紧集。由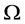 有界知,存在
有界知,存在 使得
使得
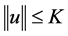 。从而对于任意的
。从而对于任意的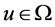 有
有
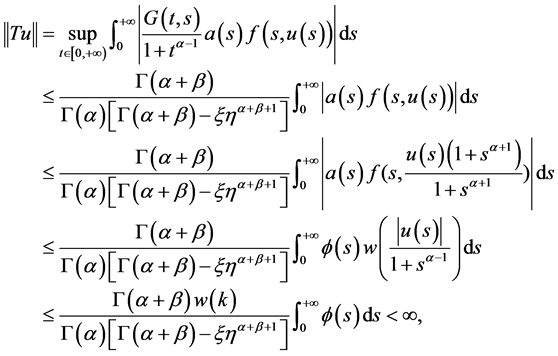
即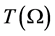 一致有界,下证
一致有界,下证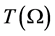 在
在 的任意紧区间上是等度连续的。
的任意紧区间上是等度连续的。
任给 ,不妨设
,不妨设 ,则对于
,则对于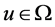 ,有
,有
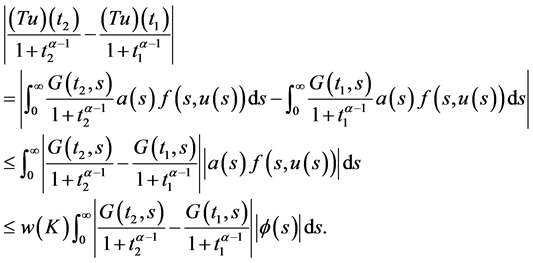
因此,对 ,存在
,存在 使得
使得 时,有
时,有

由于 是任意的,因此
是任意的,因此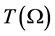 在
在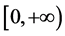 上局部等度连续。
上局部等度连续。
最后来证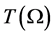 在
在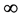 处等度收敛。任给
处等度收敛。任给 ,
,

所以
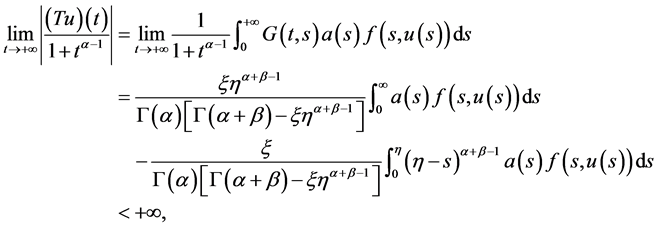
因此,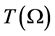 在
在 处等度收敛。
处等度收敛。
所以由引理3.4得 全连续。
全连续。
定理3.1设(H1)~(H3)成立。若(H3)中的函数 满足如下条件:
满足如下条件:
(H4)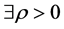 使得
使得
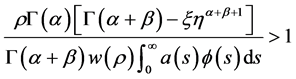 (3.3)
(3.3)
则边值问题(1.3)存在无界解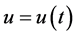 且满足
且满足
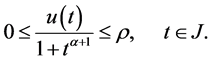
证明:考虑边值问题
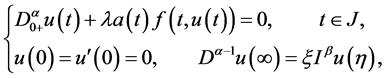 (3.4)
(3.4)
其中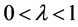 。显然,
。显然,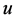 为方程(3.4)的解当且仅当
为方程(3.4)的解当且仅当 为算子方程
为算子方程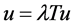 的解。
的解。
令

我们断言当 ,
, 时,
时,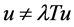 。如若不然,存在
。如若不然,存在 ,
,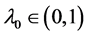 使得
使得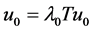 ,则
,则
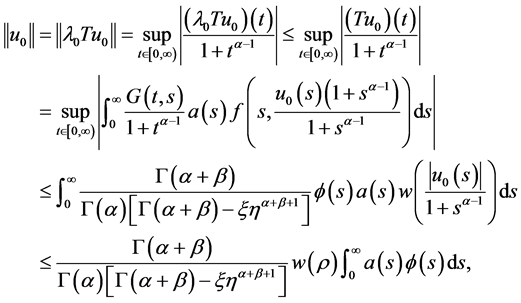
所以
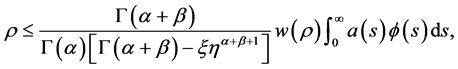
即
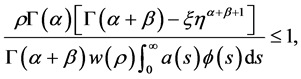
与式(3.3)矛盾。由定理2.1,边值问题(1.3)有无界解 使得
使得

证毕。
4. 多解的存在性
下面我们利用Leggett-Williams不动点定理讨论边值问题(1.3)多解的存在性。为了方便读者,我们使用以下记号:
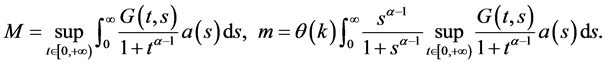
定理4.2假设条件(H1)-(H2)成立,并且假设存在常数 ,使得
,使得
(H5) ,
, ;
;
(H6) ,
,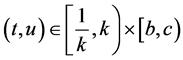 ;
;
(H7)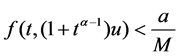 ,
, ;
;
则边值问题(1.3)至少有三个正解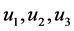 且满足
且满足

证明:定义泛函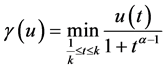 ,则
,则 为非负连续凹泛函。下证
为非负连续凹泛函。下证 全连续,连续已证,
全连续,连续已证,
现在只需要证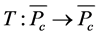 。令
。令 ,那么
,那么 ,则有
,则有

且由引理3.5知 是全连续的。同理可得
是全连续的。同理可得 时,
时, 。因此定理2.2中的条件(C2)成立。
。因此定理2.2中的条件(C2)成立。
为了验证条件(C1)成立,取 。易知
。易知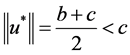 并且
并且 ,故
,故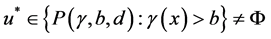 。
。
若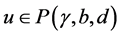 ,我们有
,我们有

因此

即 ,说明定理2.2中的条件(C2)成立。
,说明定理2.2中的条件(C2)成立。
最后,验证条件(C3)成立,假设 ,满足
,满足 ,则
,则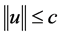 ,且有
,且有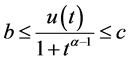 ,由
,由
(H6)我们可以得到 ,由此知定理2.2中的条件(C3)成立。故
,由此知定理2.2中的条件(C3)成立。故 至少存在三个不动点,即边值问题(1.3)至少存在三个正解
至少存在三个不动点,即边值问题(1.3)至少存在三个正解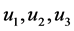 使得
使得
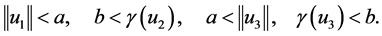
证毕。
5. 例子
例5.1令 ,则方程(1.3)变为
,则方程(1.3)变为
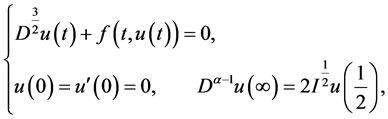 (5.1)
(5.1)
设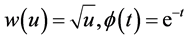 ,有
,有 ,
, ;
;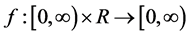 连续;
连续;
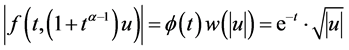 ;令
;令 ,有
,有
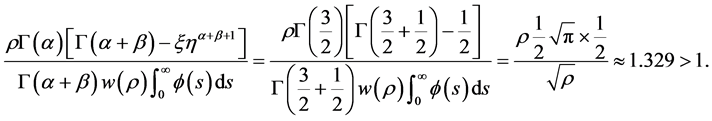
满足定理4.1,所以边值问题(5.1)存在无界解 且
且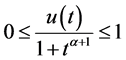 。
。
例5.2令 ,则方程(1.3)变为:
,则方程(1.3)变为:
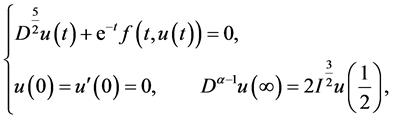 (5.2)
(5.2)
其中
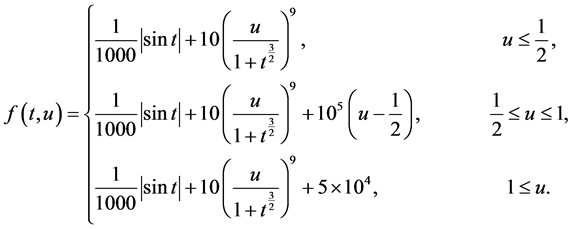
令 ,通过计算可得
,通过计算可得
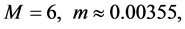
所以

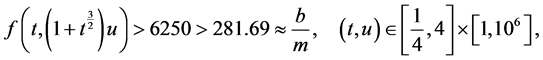

满足定理4.2,所以边值问题(5.2)至少有三个正解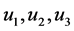 且
且


基金项目
国家自然科学基金(11361047)。
文章引用
姚佳欣,王文霞,贾建梅. 一类无穷区间上的分数阶微分方程边值问题解的存在性
The Existence of Solutions for a Class of Boundary Value Problem of Fractional Differential Equations on an Infinite Interval[J]. 理论数学, 2017, 07(04): 213-224. http://dx.doi.org/10.12677/PM.2017.74027
参考文献 (References)
- 1. 白占兵. 分数阶微分方程边值问题理论及应用[M]. 北京: 中国科学技术出版社, 2013.
- 2. Ji, Y.-D., Guo, Y.-P., et al. (2015) Existence of Positive Solutions of the Boundary Value Problem for Nonlinear Fractional Differential Equations. Journal of Advances in Difference Equations, 2015, 13. https://doi.org/10.1186/s13662-014-0335-0
- 3. Bai, Z.-B. (2000) The Method of Lower and Upper Solutions for a Bending of an Elastic Beam Equation. Journal of Mathematical Analysis and Applications, 248, 195-202.
- 4. Zhang, S.-Q. (2009) Monotone Iterative Method for Initial Value Problem Involving Riemann-Liouville Fractional Derivatives. Journal of Nonlinear Analysis, 71, 2087-2093.
- 5. Zhao, X.-K. and Ge, W.-G. (2010) Unbounded Solutions for a Fractional Boundary Value Problems on Infinite Interval. Acta Applicandae Mathematicae, 109, 495-505. https://doi.org/10.1007/s10440-008-9329-9
- 6. Wang, G.-T. (2015) Explicit Iteration and Unbounded Solutions for Fractional Integral Boundary Value Problem on an Infinite Interval. Journal of Applied Mathematics Letters, 47, 1-7.
- 7. Liu, Y.S. (2003) Boundary Value Problem for Second Order Differential Equations on Unbounded Domain. Applied Mathematics and Computation, 135, 569-583.
- 8. Liang, S.-H. and Zhang, J.-H. (2011) Existence of Three Positive Solutions of M-Point Boundary Value Problems for Some Nonlinear Fractional Differential Equations on an Infinite Interval. Journal of Computers and Mathematics with Applications, 61, 3343-3354.
- 9. Liang, S.-H. and Zhang, J.-H. (2011) Existence of Multiple Positive Solutions for M-Point Fractional Boundary Value Problems on an Infinite Interval. Journal of Mathematical and Computer Modelling, 54, 1334-1346.
- 10. Kou, C.-H., Zhou, H.-C. and Ye, Y. (2011) Existence of Solutions of Initial Value Problems for Nonlinear Fractional Differential Equations on the Half-Axis. Nonlinear Analysis, 74, 5975-5986.
- 11. Su, X.-W. and Zhang, S.-Q. (2011) Unbounded Solutions to a Boundary Value Problem of Fractional Order on the Half-Line. Computers and Mathematics with Applications, 61, 1079-1087.