ABSTRACT

In this paper, based on the GARCH(1,1)-model, we use the Pair Copula dimension reduction method to explore the correlation between the stock markets with nonlinear structure. We construct the GARCH(1,1)-models basing on four different forms of residual error distributions. We check the significance test of GARCH(1,1) with these four kinds of residual error distributions, and find out only when the residual error follows the generalized error distribution, the model passes the significance test. Therefore, we get a better choice for the edge distribution for financial asset series. With the help of Pair Copula reduction method and AIC/BIC criterion (Akaike Information Criterion/Bayesian Information Criterion), we find out that D-Vine structure is more suitable than C-Vine structure to describe the correlation between the stock markets. Finally we construct the correlation function between the stock markets basing on the D-Vine structure Pair Copula function.

Keywords:Pair Copula, GARCH(1,1), Residual Error, Stock Market

基于Pair Copula和GARCH(1,1)模型的股市 研究

张 雯，何 坤

东华大学数学系，上海

收稿日期：2019年1月8日；录用日期：2019年1月22日；发布日期：2019年1月29日

摘 要

本文在GARCH(1,1)模型的基础上，运用Pair Copula降维法探究非线性结构的股票市场间相关性。我们基于4种不同的残差分布来构建GARCH(1,1)模型，对比发现只有残差服从广义误差分布时，模型通过显著性检验，从而找到相对好的金融资产序列的边缘分布拟合模型。我们使用Pair Copula降维方法，依据AIC/BIC准则(赤池信息准则/贝叶斯信息准则)，发现D-Vine结构比C-Vine结构更适合描述股票市场间相关关系，于是最终选用D-vine结构来构建市场间相关结构的Pair Copula函数。

关键词 :Pair Copula，GARCH(1,1)，残差，股票市场

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

经济全球化的发展致使各国之间愈加紧密的经济联动，如果某一国家的金融领域发生危机，危机将在各国金融市场间快速传播。为了降低金融危机的负面影响，人们愈加重视金融市场间关联性的研究。在准确把握市场关联性的基础上进行金融对冲，投资获利的同时有效降低商业风险。

在非线性金融市场相关关系研究方面，Copula函数有着显著的优势，由Embrechts等 [1] 开创了将其应用于金融领域的先河。Copula函数的概念经由Sklar [2] 提出，文献 [3] [4] [5] [6] 对其进行进一步研究。后来为了降低高维相关性研究的难度，解决单一Copula函数的约束性，Bedford等 [7] 首次于研究中应用了藤Copula结构，Aas等 [8] 提出了藤Copula降维方法即Pair Copula降维法。

研究金融资产相关性最重要的前提条件是确定资产收益率序列的拟合模型，即边缘拟合模型。Engle Robert [9] 发明了ARCH模型(自回归条件异方差模型)，但当模型残差序列的异方差函数具有长期自相关性时，ARCH模型的拟合精度会受到影响。为此Bollerslev [10] 以ARCH模型为基础，提出了GARCH模型(广义自回归条件异方差模型)，该模型很好地描述出市场波动的异方差性和波动集群性。

在动态研究金融变量间的相依关系领域，韦艳华等 [11] 利用Copula-GARCH模型建立金融市场间的非线性相关关系，优点是边缘拟合GARCH模型残差择优服从t分布或GED分布，缺点是高维相关结构整体为Gaussian Copula函数。黄恩喜等 [12] 基于Pair Copula-GARCH-t模型研究了三只股票的相关关系，缺点是GARCH模型残差只考虑服从t分布，优点是运用藤Copula结构将高维相依分离为多个二维相依Copula，但二维Copula结构统一为t-Copula函数。宋志坚 [13] 运用Copula-GARCH模型研究国际原油价格与三种可再生能源股价的相关性，缺点是边缘拟合只考虑残差服从t分布，优点是二维相关性研究采用四种Copula函数中较适合模型。

由于，GARCH模型的残差分布影响边缘拟合的效果，在拟合边缘分布时需要多比较几种残差分布，根据模型的实际拟合效果选取较好的模型。运用C-Vine结构或D-Vine结构的Pair-Copula降维法将高维相关研究转化为多个二维相关时，两种Pair-Copula降维结构在三维时一样但其余高维存在优劣，而且转化成的二维相关性可能有各自的特点且适合不同的Copula函数。因此，本文在GARCH模型中比较了残差服从四种不同分布的情况，选出较优的边缘分布拟合模型，并在此基础上，参考李嘉琪等 [14] 研究中较全面的二维Copula函数族，使用Pair Copula降维法来研究四维股票市场联动风险特征。

2. 理论基础

2.1. Copula函数

Copula理论即可以将一个联合分布函数分解成多个边缘分布函数和一个Copula函数，适合描述多维随机变量相关关系的复杂性。

定理 [2] ：令 $F$ 为一个 $n$ 维随机向量的联合分布函数，其中各变量的边缘分布函数记为 $F_i$ ，那么一定存在一个Copula函数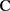，使得 $$ ，其中 $F_i\left(x_i\right)\in \left(0,1\right),i=1,\cdots ,n$ 。若边缘分布函数 $F_i$ 是连续的一元函数，则Copula函数 $C$ 的形式是唯一确定的。

Copula理论发展出了各种形式的家族函数，经常使用的类型主要分为两类：一类是椭球Copula，常用的包括Gaussian Copula和t-Copula；另外一类是由生成函数 $\phi \left(t\right)$ ( $t$ 为边缘分布)生成的阿基米德Copula，包括Clayton Copula、Gumbel Copula和Frank Copula。其中以边缘分布函数( $u,v$ )为自变量的二元Gaussian Copula、t-Copula、Clayton Copula、Gumbel Copula、Frank Copula [14] 分布函数具体的表达式分别如式(1)~(5)所示。

$C_1\left(u,v;\rho \right)={\displaystyle {\int }_{-\infty }^{{\Phi }^{-1}\left(u\right)}{\displaystyle {\int }_{-\infty }^{{\Phi }^{-1}\left(v\right)}\frac{1}{2\text{π}\sqrt{1-{\rho }^2}}\exp \left(\frac{-\left(s^2+r^2-2\rho sr\right)}{2\left(1-{\rho }^2\right)}\right)}}dsdr$ (1)

式中： ${\Phi }^{-1}(•)$ 为标准正态分布函数 $\Phi (•)$ 的逆函数；相关系数 $\rho \in \left(-1,1\right)$ ； $s,r$ 分别为 $$ 的自变量。

$C_2\left(u,v;\rho ,m\right)={\displaystyle {\int }_{-\infty }^{T_m^{-1}\left(u\right)}{{\displaystyle {\int }_{-\infty }^{T_m^{-1}\left(v\right)}\frac{1}{2\text{π}\sqrt{1-{\rho }^2}}\exp \left[1+\frac{-\left(s^2+r^2-2\rho sr\right)}{m\left(1-{\rho }^2\right)}\right]}}^{-\frac{m+2}{2}}dsdr}$ (2)

式中： $T_m^{-1}(•)$ 为自由度是 $$ 的一元t分布函数 $T_m(•)$ 的逆函数；相关系数 $$ ； $$ 分别为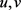的自变量。

$C_3\left(u,v;\theta \right)={\left(u^{-\theta }+v^{-\theta }-1\right)}^{-\frac{1}{\theta }}$ (3)

式中：生成函数 $\phi \left(t\right)=\frac{t^{-\theta }-1}{\theta },\theta \in \left(-1,\infty \right)\backslash \{0\}$ 。

$C_4\left(u,v;\theta \right)=\exp \left(-{\left[{\left(-\ln u\right)}^{\frac{1}{\theta }}+{\left(-\ln v\right)}^{\frac{1}{\theta }}\right]}^{\theta }\right)$ (4)

式中：生成函数 $$ 。

$C_5\left(u,v;\theta \right)=-\frac{1}{\theta }\ln \left(1+\frac{\left(e^{-\theta u}-1\right)\left(e^{-\theta v}-1\right)}{e^{-\theta }-1}\right)$ (5)

式中：生成函数 $\phi \left(t\right)=-\ln \frac{e^{-\theta t}-1}{e^{-\theta }-1},\theta \ne 0$ 。

2.2. 藤式Copula

为了降低Copula函数研究多维变量相关性的复杂程度，Aas等 [8] 提出了对Copula降维的Pair Copula分解法，即令 $X=\left[x_1,x_2,\cdots ,x_n\right]$ 为 $n$ 维随机变量，其联合分布概率密度函数可分解为式(6)。

$f\left(x_1,x_2,\cdots ,x_n\right)=f_n\left(x_n\right)\cdot f\left(x_{n-1}|x_n\right)\cdot f\left(x_{n-2}|x_{n-1},x_n\right)\cdots f\left(x_1|x_2,\cdots ,x_n\right)$ (6)

以四维随机变量为例，有星型结构的C-Vine (表达式如式(7)所示)和平行结构的D-Vine (表达式如式(8)所示)两种藤结构对其四维Copula函数进行降维。

$\begin{array}{c}f\left(x_1,\cdots ,x_4\right)=f_1\left(x_1\right)f_2\left(x_2\right)f_3\left(x_3\right)f_4\left(x_4\right)c_{12}\left(F_1\left(x_1\right),F_2\left(x_2\right)\right)\times c_{13}\left(F_1\left(x_1\right),F_3\left(x_3\right)\right)\\ \times c_{14}\left(F_1\left(x_1\right),F_4\left(x_4\right)\right)\times c_{23|1}\left(F\left(x_2|x_1\right),F\left(x_3|x_1\right)\right)\times c_{24|1}\left(F\left(x_2|x_1\right),F\left(x_4|x_1\right)\right)\\ \times c_{34|12}\left(F\left(x_3|x_1,x_2\right),F\left(x_4|x_1,x_2\right)\right)\end{array}$ (7)

$\begin{array}{c}f\left(x_1,\cdots ,x_4\right)=f_1\left(x_1\right)f_2\left(x_2\right)f_3\left(x_3\right)f_4\left(x_4\right)c_{12}\left(F_1\left(x_1\right),F_2\left(x_2\right)\right)\times c_{23}\left(F_2\left(x_2\right),F_3\left(x_3\right)\right)\\ \times c_{34}\left(F_3\left(x_3\right),F_4\left(x_3\right)\right)\times c_{13|2}\left(F\left(x_1|x_2\right),F\left(x_3|x_2\right)\right)\times c_{24|3}\left(F\left(x_2|x_3\right),F\left(x_4|x_3\right)\right)\\ \times c_{14|23}\left(F\left(x_1|x_2,x_3\right),F\left(x_4|x_2,x_3\right)\right)\end{array}$ (8)

式中： $F(\cdot )$ 为边缘分布函数； $f(\cdot )$ 为边缘密度函数； $c(\cdot )$ 是二维Pair Copula密度函数。

2.3. 边缘分布模型

采用GARCH $\left(p,q\right)$ 模型能够很好的描述收益率序列的尖峰、厚尾、非对称、波动聚集等特征，模型构建如式(9)所示。

$\{\begin{array}{l}{R}_{nt}={\mu }_n+{\epsilon }_{nt},\\ {\epsilon }_{nt}={\sigma }_{nt}{z}_{nt},\\ {\sigma }_{nt}^2={\varpi }_n+{\alpha }_{n1}{\epsilon }_{n,t-1}^2+\cdots +{\alpha }_{nq}{\epsilon }_{n,t-q}^2+{\beta }_{n1}{\sigma }_{n,t-1}^2+\cdots +{\beta }_{np}{\sigma }_{n,t-p}^2,\end{array}$ (9)

式中： ${\mu }_n$ 是第 $n$ 项收益率序列 $R_{nt}$ 的均值；误差 ${\epsilon }_{nt}$ 的条件方差是 ${\sigma }_{nt}^2$ ；残差 $z_{nt}$ 与 $$ 相互独立；常数 ${\varpi }_n>0$ ；常数 ${\alpha }_{ni}\ge 0,{\beta }_{nj}\ge 0$ 且 ${\displaystyle \sum _{i=1}^q{\alpha }_{ni}}+{\displaystyle \sum _{j=1}^p{\beta }_{nj}}<1,p>0,q>0$ ，其中 $q$ 是ARCH项的阶数、 $p$ 是GARCH项的阶数。

确保模型稳定性，将阶数设为1，则本文数据边缘拟合GARCH(1,1)模型如(10)所示。

$\{\begin{array}{l}{R}_{nt}={\mu }_n+{\epsilon }_{nt},\\ {\epsilon }_{nt}={\sigma }_{nt}{z}_{nt},\\ {\sigma }_{nt}^2={\varpi }_n+{\alpha }_{n1}{\epsilon }_{n,t-1}^2+{\beta }_{n1}{\sigma }_{n,t-1}^2,\end{array}$ (10)

式中： $$ 、 ${\varpi }_n$ 、 ${\alpha }_{n1}$ 和 ${\beta }_{n1}$ 为待估参数。

本文基于GARCH(1,1)模型拟合边缘分布，考虑了残差服从四种分布的情况，在四种残差结构中选取较优的拟合模型。如果残差 $z_{nt}$ 有 $z_{nt}\sim N\left(0,1\right)$ ，误差 ${\epsilon }_{nt}$ 有 $$ ，则构建的边缘分布函数是GARCH(1,1)-N模型；如果残差 $z_{nt}$ 有 $z_{nt}\sim t\left(m_n\right)$ ，即残差 $z_{nt}$ 符合自由度为 $m_n$ 、均值为0以及方差为1的t分布函数，则构建的边缘分布函数是GARCH(1,1)-t模型；如果残差 $z_{nt}$ 的概率密度函数如式(11)所示，则构建的边缘分布函数是GARCH(1,1)-GED；如果残差的概率密度函数如式(12)所示，则构建的边缘分布函数是GARCH(1,1)-SGED。

$f\left(x;\upsilon \right)=\frac{\upsilon \Gamma {\left(3/\upsilon \right)}^{1/2}}{2\Gamma {\left(1/\upsilon \right)}^{3/2}}\exp \left[-{\left|x\right|}^{\upsilon }{\left[\frac{\Gamma \left(3/\upsilon \right)}{\Gamma \left(1/\upsilon \right)}\right]}^{\upsilon /2}\right]$ (11)

式中： $\Gamma (\cdot )$ 为伽玛函数；形状参数 $\upsilon \in \left(-\infty ,+\infty \right)$ 为待估参数。

(12)

式中： $\text{A=}\frac{\upsilon }{\text{2B}}\text{Γ}{\left(\text{1}/\upsilon \right)}^{\text{-1}}$ ； $B=\Gamma {\left(1/\upsilon \right)}^{1/2}\Gamma {\left(3/\upsilon \right)}^{-1/2}S{\left(\lambda \right)}^{-1}$ ； $G=2\lambda \cdot D\cdot S{\left(\lambda \right)}^{-1}$ ； $S\left(\lambda \right)={\left(1+3{\lambda }^2-4D^2{\lambda }^2\right)}^{1/2}$ ； $D=\Gamma \left(2/\upsilon \right)\Gamma {\left(1/\upsilon \right)}^{-1/2}\Gamma {\left(3/\upsilon \right)}^{-1/2}$ ； $\text{sign}(\cdot )$ 为符号函数；形状参数 $\upsilon >0$ ；偏度参数 $\lambda \in \left(-1,1\right)$ 。

3. 实证研究

3.1. 数据选取及基本分析

本文选取基于A股产生的沪深300指数、新综指、中型综指和新指数的每日收盘价数据作为研究对象，选取的样本时间从2013年4月1日至2018年3月30日。数据来自锐思金融数据库(http://www.resset.cn/)，数据的研究与处理主要依靠Excel和R语言来完成。

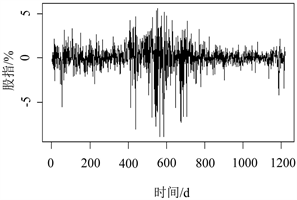
算术收益率是当期资产的价格与上一期资产的价格的差再比上上一期的资产价格的比值，对数收益率是当期资产的价格比上上一期资产的价格后再对其取对数。因为对数收益率具有时间可加性而且方便建模，所以本文采用对数收益率代表股指，表达式如式(13)所示。四种指数的对数收益率随时间的波动如图1所示。

$R_t=100\times \ln \left(P_t/P_{t-1}\right)$ (13)

式中： $t$ 是任意一个交易日； $P_t$ 定义为股指的日收盘价。

图1. 股市的四种指数的股指随时间的波动图

图1为四种指数的股指随时间的波动图。从图1可看出沪深300指数、新综指、中型综指和新指数的股指都有波动聚集的现象，即大波动紧跟着大波动、小波动紧随着小波动。

表1为股市的四种指数的对数日收益率序列的描述性统计结果。这四个指数的对数日收益率的偏度都小于0，说明这四个指数都出现了左偏的现象。而且四个指数的峰度均远大于3，表明存在“尖峰”的特征，与标准正态分布相比存在“尖峰厚尾”的现象。但是“尖峰”的特征会影响偏度的检验，故仅依据偏度和峰度的值来判断对数日收益率序列是否服从正态分布是不准确的，因此本文还进行J-B检验(Jarque-Bera test)。由J-B统计量均不服从自由度为2的卡方分布，进一步证明了收益率序列都不满足原假设，即不服从正态分布。

表1. 股市四种指数的对数日收益率描述性统计

3.2. 数据拟合

为了确保对数日收益率序列间相关关系的准确性，还要对样本数据进行检验，防止对对数日收益率序列构建边缘分布模型时出现伪回归的现象，即需通过ADF检验(augmented Dickey-Fuller test)来判断时间序列的平稳性，平稳性检验结果见表2。其中P值是t统计量对应的概率值，在1%显著性水平(犯错误概率)下，p值小于给定的显著性水平，而且t统计量小于1%显著性水平下的ADF临界值−3.43，所以时间序列不存在单位根，呈现平稳的趋势，即对数日收益率序列是平稳的时间序列。

表2. 股市四种指数的平稳性检验

考虑到对数日收益率序列的波动聚集、偏斜等的异常情况，四种指数可以通过GARCH(1,1)模型进行描述，模型残差考虑服从正态分布、学生t分布、广义误差分布和带偏广义误差分布这四种假设，四种假设下的各指数的对数日收益率序列的p值差别很大，在5%显著性水平下，正态分布和带偏广义误差分布假设下存在多个参数对应的p值大于0.05，学生t分布假设下存在一个参数p值大于0.05，广义误差分布假设下不存在，因此只有残差服从广义误差分布时才通过显著性检验。。

通过显著性检验，GARCH(1,1)-GED模型下的各指数拟合的待估参数的结果如表3。其中形状参数 $\upsilon$ 均小于2，说明股指拟合模型的残差密度函数峰度、尾部比正态分布更尖、更厚。模型拟合之后的ARCH L-M检验结果的p值大于显著性水平5%，证明了序列不存在条件异方差，说明了模型建立正确。因此本文采用GARCH(1,1)-GED模型拟合收益率序列的边缘分布。

3.3. 相关性分析

由于相关性函数Copula的性质要求，对收益率序列的拟合模型提取标准化残差，并对其进行概率积分变化，使数据落在Copula函数的自变量定义域的范围内，之后才可对变换后的新序列进行Pair Copula建模。

表3. GARCH(1,1)-GED模型的参数估计

表4为四个指数的Kendall秩相关系数的结果，可知4个指数间都存在着显著的正相关性，即其中一个指数出现大幅度的涨或跌，其他三个指数都会做出相同的反应。其中中型综指和新指数间的相关系数为0.8431，是所有相关系数中的最大值，说明了中型综指和新指数间的相互关系最强。

表4. 四个指数的Kendall秩相关系数

表5为利用AIC/BIC准则对两种不同类型Pair Copula模型拟合的结果，其中Copula函数的选择为Gaussian Copula，t-Copula，Clayton Copula，Gumbel Copula和Frank Copula [14] 。表中参数1和参数2分别为C-Vine Copula ((7)式)和D-Vine Copula ((8)式)中所选择Copula函数相对应参数的结果。根据表中AIC/BIC准则的检验结果，可以看出D-Vine模型的拟合效果优于C-Vine模型，因而通过D-Vine模型可得较优的四个指数间的联合分布的概率密度函数。

表5. C-Vine和D-Vine结构下的Copula 函数参数

4. 结语

基于Pair Copula-GARCH(1,1)模型，本文引入四种不同残差分布和GARCH(1,1)模型共同建立资产序列的边缘分布，选出较优的边缘分布拟合模型，同时Pair Copula降维产生的多个二维相关根据其相关特点选取合适的Copula函数，从而可以更准确地对股票市场进行研究。

本文的研究结果表明：1) 通过对模型参数的比较分析，发现GARCH(1,1)-GED可以很好地拟合对数收益率，形成高拟合度的边缘分布函数；2) 沪深300指数、新综指、中型综指和新指数的对数收益率曲线均符合金融市场非正态、“尖峰厚尾”的特点，且相互存在较强的正相关性；3) C-Vine和D-Vine两种模型对四维对数收益率序列Copula函数降维时，根据AIC/BIC准则，可知D-Vine更适用于拟合四个指数间的相关关系；4) 根据D-Vine结构拟合出的四个指数间的概率密度函数，可以得到联合概率分布，对四个指数间的相互变化关系有大致的预判，从而当市场发生变化时，有助于作出适合自身的决策。

文章引用

张 雯,何 坤. 基于Pair Copula和GARCH(1,1)模型的股市研究
Research of Stock Market Based on Pair Copula and GARCH(1,1) Model[J]. 理论数学, 2019, 09(02): 129-136. https://doi.org/10.12677/PM.2019.92016

参考文献