Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30066
,
11
pages
10.12677/PM.2019.93031
Classical Solutions to the Compressible Non-Newtonian Fluids with Power-Law Viscous
Xiaojuan Huang
Department of Mathematics, Shanghai University, Shanghai

Received: Apr. 9th, 2019; accepted: Apr. 20th, 2019; published: May 5th, 2019

ABSTRACT
In this paper, a one-dimensional compressible non-Newtonian fluid model on a bounded interval is studied. If the initial density has a positive lower bound, the local existence of the classical solutions for the initial boundary value problem of a non-Newtonian fluid model with Power-Law viscous is proved by constructing approximate solutions and applying energy estimation.
Keywords:Compressible Non-Newtonian Fluids, Power-Law Viscous, Classical Solution
带有Power-Law型粘性项的 可压缩非牛顿流的光滑解
黄晓娟
上海大学理学院数学系,上海

收稿日期:2019年4月9日;录用日期:2019年4月20日;发布日期:2019年5月5日

摘 要
本文研究一维有界区间上的可压非牛顿流体模型。在初始密度有正下界的情况下,通过构造逼近解,应用能量估计,得到了带有Power-Law结构粘性项的非牛顿流模型初边值问题光滑解的局部存在性。
关键词 :可压缩非牛顿流,Power-Law 型粘性项,光滑解

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在这篇文章中,我们研究如下可压非牛顿流模型,
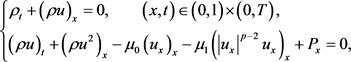 (1.1)
(1.1)
初边值条件:
 (1.2)
(1.2)
其中
和
表示的是未知的密度、速度和压力,
是常数。为了简化计算,我们可假设
。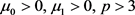 为给定常数。
为给定常数。
非牛顿流体的研究涉及到很多重要的领域,例如化学、生物、冰川、地质等,因此得到了许多专家的关注,上世纪七十年代Ladyzhenskaya [1] 和Lions [2] 证明了不可压缩非牛顿流模型的Dirichlet弱解存在性,这是此类问题最早的结果。
对于可压缩非牛顿流模型,文献 [3] [4] [5] 中研究了当空间维数
时测度值弱解的存在性。Feireisl,Liao和Málek在文献 [6] 中提出了相关初边值问题弱解的全局存在性。另外,Mamontov在文献 [7] 中研究了一维和二维空间中全局解的存在性。近些年来,关于一维空间下的可压缩非牛顿流问题强解的适定性研究取得了一些进展。在一维空间且允许真空出现时,Yuan和Xu证明了局部强解的存在唯一性(见 [8] [9] )。而在
的条件下,局部光滑解的存在性问题已经被Fang和Li证明(见 [10] )。更多相关结论,可以参考文献 [11] [12] [13] 。
本文将研究具有Power-Law型粘性项的一维可压缩非牛顿流光滑解的存在唯一性。在这里我们考虑初始密度具有正下界的情况。
我们的主要结论如下:
定理 1:假设
,初值
满足
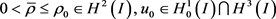 (1.3)
(1.3)
其中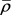 为常数,那么存在一个时间
为常数,那么存在一个时间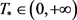 ,对于初边值问题(1.1)~(1.2)存在局部光滑解
,对于初边值问题(1.1)~(1.2)存在局部光滑解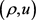 且满足:
且满足:
(1.4)
本文共有三部分,在第二部分,我们将通过迭代的方法构造逼近方程,并得到逼近解的先验估计。定理1的证明将在第三部分完成。
2. 先验估计
为了得到光滑解的存在性,需要先进行解的正则性估计。在这一部分,我们构造了方程组(2.1)~(2.2)的一个近似解,并得到了近似解的正则性估计,最后证明了近似解的收敛性。
2.1. 构造近似解
首先,我们通过迭代法构造近似解。假设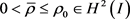 ,
,
· 定义
。
· 对
,给定
,则由 [9] ,我们得到下列模型的光滑解
:
(2.1)
(2.2)
初边值条件如下
(2.3)
接下来,我们将证明近似解的一致能量估计。
2.2. 近似解的一致估计
为了简化计算,我们首先定义
为:
应用 [12] 中类似的方法,我们可以得到逼近解
如下能量估计。
引理1:若
是(2.1)~(2.2)的光滑解,那么存在
,使得
(2.4)
其中
仅与
有关。
为了得到问题的光滑解,我们需要证明逼近解
的高阶能量估计。
引理2:若
是(2.1)~(2.2)的光滑解,则存在仅与
有关的
,使得
(2.5)
证明:应用
乘以方程(2.1)两端,我们得到
(2.6)
接下来对(2.6)式关于x求导得
(2.7)
由(2.4)式,(2.7)式和Sobolev不等式,可以推出
(2.8)
进一步地,我们对(2.7)式关于x求导,有
(2.9)
方程(2.9)两边同乘以
,并在(0, 1)上关于x积分有
(2.10)
另一方面,由(2.2)式,
(2.11)
这蕴含
(2.12)
进一步,我们有
应用Sobolev嵌入定理和Hölder不等式,我们得到
因此,我们有
(2.13)
联立(2.4)式,(2.10)式,和(2.13)式,可以得到
应用Gronwall’s不等式,我们可以证明存在
,使得
(2.14)
由(2.8)式,可以推得
应用同样的方法,我们可以得到
的估计
(2.15)
其中
。
引理得证。
引理3:假定
是方程(2.1)~(2.2)的光滑解,则
(2.16)
对任意的
都成立。
证明:首先,为了证明的需要,我们定义如下函数
这里,
是某一个足够大的正整数。
对(2.1)式关于t求导,得到
(2.17)
应用引理1和2,可以证明
类似地,我们还可以得到P的估计
(2.18)
由(2.13)式,我们得到,
接下来,我们对(2.2)式关于t求导,
(2.19)
由上式可以得到如下估计,
接下来,我们估计
。用
乘以方程(2.19)两端,并在(0, 1)上关于x积分,可得
(2.20)
应用Young不等式和Sobolev不等式,我们得到
这里我们还用到了引理1和2的结论。将上述估计代入(2.20)式得到
(2.21)
另一方面,由于
,结合引理1,我们得到如下结论
我们定义一个函数
:
由引理1和2得
应用引理1,对(2.21)式关于t在(0, t)上积分,得到
(2.22)
所以
(2.23)
容易证明存在
,使得
(2.24)
收集所有的估计,我们可以得到
(2.25)
引理得证。
最后,总结引理1~3,我们有如下结论:对
,下式成立,
(2.26)
2.3. 逼近解的收敛性
在这一部分,将证明我们所构造的逼近解的收敛性。
令
那么
满足下列方程:
(2.27)
(2.28)
其初边值条件为
(2.29)
方程(2.27)两边同乘以
并关于x在(0, 1)上积分,结合估计(2.26)可得
(2.30)
对任意的
和
都成立。
另外将方程(2.28)两边同乘以
并关于x在(0, 1)上积分得
(2.31)
联立(2.30)式和(2.31)式,我们有
我们对上式关于
求和,在
上关于t积分,选取足够小的
并应用Gronwall’s不等式有
(2.32)
联立上式和(2.26)式,应用Gagliardo-Nirenberg不等式可以得出,当
时,序列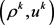 收敛于
,其中
为序列
的极限。易证明
是方程(2.1)~(2.2)的解,且满足以下正则性估计:
收敛于
,其中
为序列
的极限。易证明
是方程(2.1)~(2.2)的解,且满足以下正则性估计:
(2.33)
3. 定理1的证明
这一部分,我们将证明定理1。首先因为
,应用特征线方法可以从(2.1)中推出
.
由(2.34)式,我们可以得到(1.1)~(1.2)的解
满足
(3.1)
然后,由
的连续性,又因为
和
,我们有
。由(1.1)式和(3.1)式,可以得到
(3.2)
由(3.2)式和(1.1)式,结合
的正则性估计,可得
(3.3)
联合(1.1)式、(3.2)式和(3.3)式,我们有
(3.4)
对(1.1)式进行求导,有
,所以
(3.5)
进一步地,由
的正则性估计,我们可以得到
(3.6)
则定理1中局部光滑解的存在性得证。关于解的唯一性可参考文献 [9] ,我们这里不再赘述。定理1得证。
文章引用
黄晓娟. 带有Power-Law型粘性项的可压缩非牛顿流的光滑解
Classical Solutions to the Compressible Non-Newtonian Fluids with Power-Law Viscous[J]. 理论数学, 2019, 09(03): 243-253. https://doi.org/10.12677/PM.2019.93031
参考文献
- 1. Ladyzhenskaya, O.A. (1970) New Equations for the Description of the Motions of Viscous Incompressible Fluids and Global Solva-bility for Their Boundary Value Problems. Trudy Matematicheskogo Instituta imeni V. A. Steklova, 102, 85-104.
- 2. Lions, P.L. (1998) Mathematical Topics in Fluid Mechanics: Compressible Models. Clarendon Press, Oxford.
- 3. Necas, J. (1990) Theory of Multipolar Viscous Fluids. The Mathematics of Finite Elements and Applications, 7, 233-244.
- 4. Necas, J. and Novotny, A. (1994) Measure-Valued Solution for Non-Newtonian Compressible Isothermal Monopolar Fluid. Acta Applicandae Mathematica, 37, 109-128.
https://doi.org/10.1007/BF00995134
- 5. Neckcasova, S. and Lukacova, M. (1994) Bipolar Barotropic Non-Newtonian Fluid. Commentationes Mathematicae Universitatis Carolinae, 35, 467-483.
- 6. Feireisl, E., Liao, X. and Malek, J. (2015) Global Weak Solutions to a Class of Non-Newtonian Compressible Fluids. Mathematical Methods in the Applied Sciences, 38, 3482-3494.
https://doi.org/10.1002/mma.3432
- 7. Mamontov, A.E. (1999) Global Solvability of Multidimensional Navier-Stokes Equations of Compressible Nonlinearly Viscous Fluid. I. Siberian Mathematical Journal, 40, 351-362.
https://doi.org/10.1007/BF02679762
http://apps.webofknowledge.com/full_record.do?product=UA&search_mode=GeneralSearch&qid=4&SID=6Cb5e1i8fXVsPmEc3eL&page=1&doc=1
- 8. Yuan, H.J. and Xu, X.J. (2008) Existence and Uniqueness of Solutions for a Class of Non-Newtonian Fluids with Singularity and Vacuum. Journal of Differential Equations, 245, 2871-2916. https://doi.org/10.1016/j.jde.2008.04.013>http://www.elsevier.com/locate/jde
https://doi.org/10.1016/j.jde.2008.04.013
- 9. Yuan, H.J. and Li, H.P. (2012) Existence and Uniqueness of Solution for a Class of Non-Newtonian Fluids with Vacuum and Damping. Journal of Mathematical Analysis and Applications, 391, 223-239.
>https://www.sciencedirect.com/science/article/pii/S0022247X12001084?via%3Dihub
https://doi.org/10.1016/j.jmaa.2012.02.015
- 10. Fang, L. and Li, Z.L. (2015) On the Existence of Local Classical Solution for a Class of One-Dimensional Compressible Non-Newtonian Fluids. Acta Mathematica Scientia (English Series), 35, 157-181.
https://doi.org/10.1016/S0252-9602(14)60148-X
- 11. Fang, L., Guo, Z.H. and Wang, Y.X. (2016) Local Strong Solutions to a Compressible Non-Newtonian Fluid with Density-Dependent Viscosity. Mathematical Methods in the Applied Sciences, 39, 2583-2601.
>https://onlinelibrary.wiley.com/doi/pdf/10.1002/mma.3714
https://doi.org/10.1002/mma.3714
- 12. 杨迪, 佟丽宁. 真空下一维可压的非牛顿Ellis模型解的存在唯一性[J]. 应用数学与计算数学学报, 2017, 31(1): 128-142. http://qikan.cqvip.com/article/detail.aspx?id=671559827
- 13. Yin, L., Xu, X.J. and Yuan, H.J. (2008) Global Existence and Uniqueness of Solution of the Initial Boundary Value Problem for a Class of Non-Newtianian Fluids with Vacuum. Zeitschrift fur Angewandte Mathematik und Physik, 59, 457-474.
https://doi.org/10.1007/s00033-006-5078-7







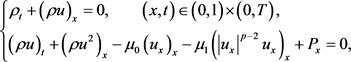 (1.1)
(1.1) (1.2)
(1.2)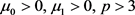 为给定常数。
为给定常数。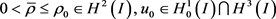 (1.3)
(1.3)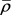 为常数,那么存在一个时间
为常数,那么存在一个时间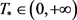 ,对于初边值问题(1.1)~(1.2)存在局部光滑解
,对于初边值问题(1.1)~(1.2)存在局部光滑解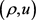 且满足:
且满足: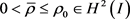 ,
,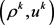 收敛于
,其中
为序列
的极限。易证明
是方程(2.1)~(2.2)的解,且满足以下正则性估计:
收敛于
,其中
为序列
的极限。易证明
是方程(2.1)~(2.2)的解,且满足以下正则性估计: