Pure Mathematics
Vol.
09
No.
05
(
2019
), Article ID:
31194
,
6
pages
10.12677/PM.2019.95074
Congruences on Normal Cryptic rpp Semigroups
Wenjuan Guo1, Xiaojiang Guo2
1School of Education, Jiangxi Normal University, Nanchang Jiangxi
2College of Mathematics and Information Science, Jiangxi Normal University, Nanchang Jiangxi

Received: Jun. 13th, 2019; accepted: Jul. 2nd, 2019; published: Jul. 9th, 2019

ABSTRACT
The aim of this note is to study congruences on cryptic rpp semigroups. Some properties of traces of L*-unary congruences on this class of semigroups are obtained. Also, some special cases are considered.
Keywords:rpp Semigroup, Cryptic rpp Semigroup, Unary Congruence, Trace
密码rpp半群上的同余
郭文娟1,郭小江2
1江西师范大学教育学院,江西 南昌
2江西师范大学数学与信息科学学院,江西 南昌

收稿日期:2019年6月13日;录用日期:2019年7月2日;发布日期:2019年7月9日

摘 要
本文的主要目的是研究密码rpp半群的同余,得到了这类半群上的L*-酉同余迹的一些性质。另外,也考虑了一些特殊L*-酉同余。
关键词 :rpp半群,密码rpp半群,酉同余,迹

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言和准备
称半群S为右主投射半群(简称rpp半群),如果对于任意的 ,作为S1-系,aS1总是投射的。对偶地,定义左主投射半群(lpp半群)。作为完全正则半群(completely regular semigroup)的推广,郭聿琦,岑嘉评,朱聘瑜 [1] 定义了强rpp半群(strongly rpp semigroup)。之后,有一系列论文从事这一课题的研究(参见, [2] - [22] )。类似于密码群(cryptogroup),郭小江,杨艳萍 [12] [20] 定义了密码rpp半群(cryptic rpp semigroup),并且给出了这类半群的结构。同余理论是半群理论的重要组成部分,同余性质可以很好地表达半群的结构信息,因此研究半群上的同余是有意义的。本文将考虑密码rpp半群的同余问题。事实上,对密码rpp半群的同余理论,已经做了些探索(见 [8] )。
作为通常Green-关系的推广,我们有
众所周知,
为右同余,
为左同余。一般地,
,。但当a,b都是正则元时, 当且仅当
。等价地,半群S为rpp半群当且仅当对于任意的
,都存在幂等元e使得
当且仅当
。等价地,半群S为rpp半群当且仅当对于任意的
,都存在幂等元e使得 。易知,正则半群是rpp半群。
。易知,正则半群是rpp半群。
定义1.1:一个rpp半群S称为强rpp半群(strongly rpp semigroup),如果对于任意的 ,都存在惟一幂等元 ,使得 且 。
对偶地,定义强lpp半群(strongly lpp semigroup)。为更好地研究强rpp半群,郭小江,郭聿琦,岑嘉评 [5] [6] 定义了如下关系。令S为强rpp半群, ,定义
郭小江,郭聿琦,岑嘉评证明了:
1) ;
2) ;
3) 对于任意的正则元 ,。
一般地, 不是S上的左同余。如果 为S上的左同余,则称S为超rpp半群(super rpp semigroup) (见 [6] )。事实上,一个强rpp半群为超rpp半群的充分必要条件是它上的 关系为半格同余。
定义1.2:强rpp半群S称为密码rpp半群(cryptic rpp semigroup),如果 为S上的同余。finition
郭小江,杨艳萍 [12] 指出:密码rpp半群都是超rpp半群,并且密码群恰为正则的密码rpp半群。关于密码群,参见 [23] )。叶火平,郭俊颖,郭小江 [21] 证明了:一个超rpp半群的所有正则元构成一个完全正则半群。这表明,一个密码rpp半群的所有正则元构成一个密码群。
定义1.3:半群S上的同余 称为 -同余( -congruence),如果对于任意的 , 蕴含着 。
定义1.4:强半群S上的同余 称为酉同余(unary congruence),如果对于任意的 , 蕴含着 。
引理1.5 ( [8] ,引理7):令S为强rpp半群。若
为S上的
-酉同余,则
为强rpp半群,且
, 。
。
本文将采用教科书 [24] 的概念和术语,未给出定义的可参见文献 [6] 。
2. 迹
本节将研究密码rpp半群上同余的性质。首先,回忆同余迹的定义。
定义2.1:令S为半群, 为S上的同余。称E(S)(S的幂等元集)上的等价关系 为同余 的迹。
为得到密码rpp半群同余迹的一般性质,引进如下概念。
定义2.2:E(S)上等价关系 称为正规的(nomral),如果
(T)
进一步,E(S)上的正规等价关系 称为真的(proper),如果 既不为恒等关系 ,也不是泛关系 。
明显,E(S)上的恒等关系 和泛关系 都是正规的。记JN(S)为E(S)上所有正规等价关系所组成的集合,并赋予集合的包含关系。
据定义,不难验证,有如下推论:
推论2.3:E(S)上的正规等价关系的交还是正规的。
基于推论2.3,可以证得下面引理。
引理2.4:关于如下运算:对于
是完备格。
证明:据推论2.3, 与 均为E(S)上的正规等价关系。因此
和
都是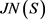 上代数运算。据此,易知:
为一个完备格。
上代数运算。据此,易知:
为一个完备格。
下面是本节的主要结果。
定理2.5:令S为密码rpp半群。对于E(S)上的等价关系 ,以下各款等价:
(i) 为正规的;
(ii) ,其中 为含于 的最大同余;
(iii) 存在S上的 -酉同余 ,使得 ;
(iv) ,其中 为包含 的最小 -酉同余。
而且,如果条件(i)~(iv)满足,那么S上以 为迹的 -酉同余均包含在区间 。
证明:(i)⇒(ii)显然, 为自反的,对称的。令 且 ,则存在 使得 。而 ,进而 ,因此 ,故 。
这样, 为传递的。
记 。令 ,则对于任意的 ,,进而 ,从而 ,显然 ,反之,若 ,则 ,进而存在 使得 ,从而 。但一个H-类最多含有一个幂等元,从而 ,故 ,这样 。现在证明了: 。
(ii)⇒(iii)。用(i)⇒(ii)证明中的符号,仅需证明: 为 -酉同余。
令 ,由 ,知 。对于任意的 ,
1) 若 ,即 ,则对于任意的 ,,从而存在 使得 。但 为S上的同余,于是
。
因此 。
2) 若 ,则 ,再根据(1),有
综合(1),(2),已经证明了:对于任意的 ,
从而 ,故 为 -同余。
设 ,那么 使得 ,进而 ,于是 ,从而 ,,因此 。故 为酉同余。
(iii)⇒(iv)。明显,
,进而
。若
,则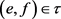 ,从而
,这样
,故
。
,从而
,这样
,故
。
(iv) ⇒(i)。因为
对于任意
(由于 为酉同余)
所以 为正规等价关系。
现在假设条件(i)~(iv)成立。令 为S上的 -同余,且 ,则 。对于任意的 ,且 ,由 ,从而 ,因此 ,进而 。反之,若 ,则由条件(ii),(iv),
故 。
3. 几类L*-酉同余
本节考虑密码rpp半群上的几类重要同余。
半群S上的同余 称为幂等元分离(idempotent-separating),如果对于任意 , 蕴含着 。等价地说, 为幂等元分离同余的充分必要条件是 (E(S)上的恒等关系)。
命题3.1:令S为密码rpp半群, 为S上的 -酉同余,则 为幂等元分离同余的充分必要条件是 。
证明:(充分性)设 。对于任意的 ,若 ,进而 ,从而 ,故 为幂等元分离同余。
(必要性)设 为幂等元分离同余,那么 ,据定理2.5, 。
半群S上的同余 称为左消幺半群同余(left cancellative monoid congruence),如果 为左消幺半群。不难验证,对于rpp半群,任一左消幺半群同余都是 -酉同余。
命题3.2:令S为密码rpp半群, 为S上的 -酉同余,则 为左消幺半群同余的充分必要条件是 。
证明:设 为左消幺半群同余,则 有且仅有一个幂等元。易知,对于任意的 , 是 的幂等元,因此 ,故 ,于是 。
反之,若
,则根据引理1.5,
有且仅有一个幂等元。因此
为幺半群。但
为强rpp半群,所以
为左消幺半群,故 为S上的左消幺半群同余。
为S上的左消幺半群同余。
下面是命题3.2的直接推论。
推论3.3:令S为密码rpp半群,则 是S上的最小左消幺半群 -酉同余。
Rpp半群S称为C-rpp半群,如果E(S)在S的中心内。等价地,一个半群为C-rpp半群的充分必要条件是它为一些左消去幺半群的强半格。值得指出,一个C-rpp半群的所有正则元构成一个子半群,并且为Clifford半群(即,所有幂等元都在其中心的正则半群)。关于Clifford半群,参见( [24] , p. 93)。
半群S上的同余 称为S上的C-rpp半群同余,如果 为C-rpp半群。
引理3.4:令S为密码rpp半群, 为S上的 -酉同余。对于任意的 ,若 ,则 。
证明:由定义,知 ,于是 。据引理1.5, ,。因此 ,从而 。
命题3.5:令S为密码rpp半群, 为S上的 -酉同余,则 为C-rpp半群同余的充分必要条件是 。
证明:(必要性)设 为C-rpp半群同余,若 ,于是存在 使得 ,从而 。但 的所有正则元组合Clifford子半群,所以 ,因此 。反之,记RegS为S的所有正则元组合的集合。由S为密码rpp半群,知S为超rpp半群,于是RegS为完全正则子半群,易知, 为RegS上的Clifford半群同余,再据( [23] , p. 257, Exercises VI.2.13(i)), 。若有 ,显然, ,于是 ,从而 。故 。
(充分性)假设 。注意到,RegS为密码群,再根据引理1.5,要证 为C-rpp半群,仅需证: 为Clifford半群。又 蕴含着 ,再由( [23] , p. 257, Exercises VI.2.13(i)), 为Clifford半群。从而 为C-rpp半群,即 为C-rpp半群同余。
基金项目
国家自然科学基金项目(11761034, 11361027, 11661042)和江西省自然科学基金项目(20161BAB201018)资助。
文章引用
郭文娟,郭小江. 密码rpp半群上的同余
Congruences on Normal Cryptic rpp Semigroups[J]. 理论数学, 2019, 09(05): 557-562. https://doi.org/10.12677/PM.2019.95074
参考文献
- 1. Guo, Y.Q., Shum, K.P. and Zhu, P.Y. (1995) The Structure of Left C-rpp Semigroups. Semigroup Forum, 50, 9-23.
https://doi.org/10.1007/BF02573502 - 2. Guo, J.Y., Guo, X.J. and Ding, J.Y. (2015) Completely J(ℓ)-Simple Semigroups. Advances in Mathematics (China), 44, 710-718.
- 3. Guo, J.Y., Guo, X.J. and Ding, J.Y. (2015) Free Completely J(ℓ)-Simple Semi-groups. Acta Mathematica Sinica, English Series, 31, 1086-1096.
https://doi.org/10.1007/s10114-015-4117-8 - 4. Guo, X.J. (2000) The Structure of NBe-rpp Semigroups. Northeastern Mathematical Journal, 4, 398-404.
- 5. Guo, X.J., Guo, Y.Q. and Shum, K.P. (2008) Rees Matrix Theorem for D(ℓ)-Simple Strongly Rpp Semigroups. Asian-European Journal of Mathematics, 1, 215-223.
https://doi.org/10.1142/S1793557108000205 - 6. Guo, X.J., Guo, Y.Q. and Shum, K.P. (2010) Super Rpp Semigroups. Indian Journal of Pure and Applied Mathematics, 41, 505-533.
https://doi.org/10.1007/s13226-010-0030-0 - 7. 郭小江. 满足置换恒等式的强rpp半群的结构[J]. 科学通报, 1996, 41(18): 1647-1650.
- 8. 郭俊颖, 郭小江, 叶火平. 正规密码rpp半群上的同余[J]. 江西师范大学学报: 自然科学版, 2017, 41(4): 360-366.
- 9. Guo, X.J., Jun, Y.P. and Zhao, M. (2010) Pseudo-C-Rpp Semi-groups. Acta Mathematica Sinica, 26, 629-646.
https://doi.org/10.1007/s10114-010-8030-x - 10. Guo, X.J., Shum, K.P. and Guo, Y.Q. (2001) Perfect Rpp Semigroups. Com-munications in Algebra, 29, 2447-2459.
https://doi.org/10.1081/AGB-100002400 - 11. 郭小江, 吴爱军. 关于左C-Rpp半群的一点注记[J]. 江西师范大学学报: 自然科学版, 2005, 29(4): 283-286.
- 12. Guo, X.J. and Yang, Y.P. (2013) Cryptic Rpp Semigroups. Advances in Mathematics (China), 42, 465-474.
- 13. Guo, X.J., Zhao, M. and Shum, K.P. (2008) Wreath Product Structure of Left C-Rpp Semigroups. Algebra Collo-quium, 15, 101-108.
https://doi.org/10.1142/S1005386708000102 - 14. 郭聿琦, 岑嘉评, 朱聘瑜. 左C-rpp半群的结构[J]. 科学通报, 1992(4): 292-294.
- 15. 郭聿琦. 左C-rpp半群的右对偶[J]. 科学通报, 1997(19): 1599-1603.
- 16. He, Y., Guo, Y.Q. and Shum, K.P. (2004) The Construction of Orthodox Super Rpp Semigroups. Science in China, 17, 552-565.
https://doi.org/10.1360/02ys0365 - 17. Shum, K.P., Guo, X.J. and Ren, X.M. (2000) ${(\ell)}$-Green’s Relations and Perfect Rpp Semigroups. In: Sunada, T., Polly, W.S. and Yang, L., Eds., Proceedings of the 3th Asian Mathematical Conference, 604-613.
- 18. Shum, K.P. and Ren, X.M. (2004) The Structure of Right C-Rpp Semigroups. Semigroup Forum, 68, 280-292.
https://doi.org/10.1007/s00233-003-0012-1 - 19. Wang, J.Q., Guo, X.J. and Qiu, X.W. (2014) Regular OS-Rpp Semigroups. Bulletin of the Malaysian Mathematical Sciences Society, 37, 597-610.
- 20. Yang, Y.P. and Guo, X.J. (2009) Orthocryptic Rpp Semigroups. International Mathematical Forum, 42, 2065-2074.
- 21. 叶火平, 郭俊颖, 郭小江. 超rpp半群的核心[J]. 理论数学, 2016(6): 172-176.
- 22. 王莹, 郭俊颖, 吴灏驰, 郭小江. 密码rpp半群的若干特征[J]. 江西师范大学学报: 自然科学版, 2019, 43(1): 22-27.
- 23. Petrich, M. and Reilly, N.R. (1999) Completely Regular Semigroups. John Wiley & Sons, New York.
- 24. Howie, J.M. (1976) An Introduction to Semigroup Theory. Academic Press, London.