Pure Mathematics
Vol.
09
No.
06
(
2019
), Article ID:
31572
,
6
pages
10.12677/PM.2019.96089
Optimization of Solution Methods for Straight Lines and Conic Curves Passing Focus
Wenli Hu, Dexiang Sun
College of Mathematics and Computer Science, Aba Normal University, Wenchuan Sichuan

Received: Jul. 8th, 2019; accepted: Jul. 18th, 2019; published: Aug. 2nd, 2019

ABSTRACT
The combination of straight line and conic is often used as the content of college entrance examination. The types of questions are varied and the calculation process is complicated. It is often a kind of questions difficult for students to master. Based on this, this paper introduces a simple calculation of the correlation between straight line and conic through focus.
Keywords:Straight Line, Conical Curve, Problem Solving Method, Optimization
过焦点的直线与圆锥曲线的解题方法的 优化
胡文利,孙德祥
阿坝师范学院数学与计算机科学学院,四川 汶川

收稿日期:2019年7月8日;录用日期:2019年7月18日;发布日期:2019年8月2日

摘 要
直线与圆锥曲线相结合的题常作为高考内容,问题出题类型变化多,运算过程复杂,往往是学生较难掌握的一类题型。基于此,本文介绍了一种经过焦点的直线与圆锥曲线的相关计算的简便运算。
关键词 :直线,圆锥曲线,解题方法,优化

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在直线与圆锥曲线的问题中,传统的基本思维都是在观察直线与圆锥曲线性质之后,运用联立方程组、合理设元、点差法、化繁为简数形结合法在其性质的基础之上求解 [1] ,求解过程复杂且没有针对性。在本文中,我们首先推出了关于直线与圆锥曲线相交的三条定理,接着,介绍了三条定理的运用。这些定理简便了圆锥曲线的运算过程,且针对直线与圆锥曲线相交的问题做了系统的解说与证明,使得学生在解题时能够更加轻松地解出正确的答案。
其中的三个定理为:
定理1 设椭圆 ,其中( )的离心率为e,且斜率为k的直线过该椭圆的焦点F,与椭圆相交于A、B,若 ,则 。
定理2 设双曲线 的离心率为e,斜率为k的直线过该双曲线的焦点F,与双曲线交于A、B两点,若 ,则 。
定理3 已知抛物线 ( ), ,斜率为k的直线过抛物线的焦点F,与抛物线相交
于A、B,若 ,则 ( )。
2. 主要结论的证明
定理1的证明
设A、F、B的坐标分别为 , , ,
所以 , 。又 。 ,
则 ,
把上式代入方程中有: , , ,则 。
所以, , ,又 ,
则: ,
,
, 。
则 。
又 ,
,化简得: ,
移项得:
解得:
定理2的证明
证明方法同定理1。
定理3的证明
1) 设A,B,F的坐标分别为: , , ,
有 , 。
则 ,
, , ,
则 ,
又 , ,
化简得 , , ,
则 ,解得: 。
2) 设 , , ,
有向量 , 。
则 。
又 , , ,则
又 , ,
代入方程
解得:
3. 定理的应用
例1 已知椭圆 ,其中 ,离心率为 ,斜率为k (k > 0)圆的右焦点F与椭圆
相交于A、B,且 求斜率k的值。
传统方法 [2] :设方程的一般形式,再利用韦达定理求解,非常麻烦,且运算量也特别大。
优化方法:由公式代入 , 可得, ,则
,故 。
又 , 。
例2 双曲线右焦点为F,F斜率为 的直线交双曲线于A、B,求双曲线离心率。
传统方法:如图1,过点A、B、F分别做垂线交准线与P、Q、R
直线AB斜率为 ,即 ,
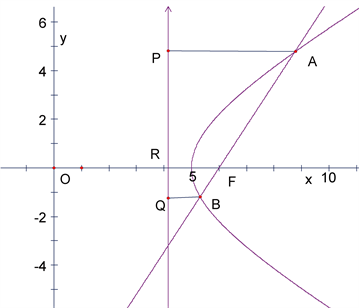
Figure 1. The relation diagram of straight line and directrix passing through hyper-bolic focal point
图1. 过双曲线焦点的直线与准线关系图
直线倾角 。由离心率定义有: 。
设 , ,已知 ,由图中几何关系可知,有:
, ,
,即 ,化简,解得 。
双曲线的离心率为 。
优化方法:由公式代入 , ,则 ,于是, ,因此 。
例3抛物线y² = 2px的焦点为F,见图2。直线交抛物线于F,且 ,则该直线的倾斜角为多少?
传统方法:当点A在第一象限、点B第四象限时,过A、B分别作准线的垂线,垂足分别为M、N,作BC⊥AM,垂足为C,设 , ,则由抛物线得 , 。
, 。
,于是直线l的倾斜角为60˚,斜率 ,故该直线的倾斜角为 。
当点A第四象限、点B第一象限时,同理可以求得直线的斜率 ,该直线的倾斜角为 。故答案为 或 。
优化方法:由公式代入 , ,则 ,于是 ,
则该直线的倾斜角为 或 。

Figure 2. The relation diagram between the straight line passing through the focus of parabola and the directrix
图2. 过抛物线焦点的直线与准线的关系图
4. 结语
圆锥曲线问题的求解方法远远不止这些,上述结论中只优化了圆锥曲线中过焦点直线这类问题,简便了运算,节省了运算时间。
致谢
作者衷心感谢阿坝师范学院数学与计算机科学学院杨仕椿教授的悉心指导!
基金项目
阿坝师范学院教学改革研究项目(20170203, 20171510, 20171515)。
文章引用
胡文利,孙德祥. 过焦点的直线与圆锥曲线的解题方法的优化
Optimization of Solution Methods for Straight Lines and Conic Curves Passing Focus[J]. 理论数学, 2019, 09(06): 673-678. https://doi.org/10.12677/PM.2019.96089
参考文献
- 1. 林丽平. 常用直线与圆锥曲线解题方法简介[J]. 教育教学论坛, 2014(47): 258-259.
- 2. 张家辉. 圆锥曲线在高考试题中的总结与解题策略[J]. 科技经济导刊, 2018, 26(27): 131-132.