Pure Mathematics
Vol.
09
No.
09
(
2019
), Article ID:
32842
,
9
pages
10.12677/PM.2019.99125
A Classification on a Class of Vertex Quasiprimitive and Bi-Quasiprimitive Cubic Symmetric Graphs
Junjie Huang
School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan

Received: Oct. 9th, 2019; accepted: Oct. 30th, 2019; published: Nov. 6th, 2019

ABSTRACT
Let be a graph and . Then is called a G-basic graph, if G is quasiprimitive or bi-quasiprimitive on vertex set . In this paper, we classify cubic symmetric G-basic graphs of order , where are primes, and .
Keywords:Symmetric Graph, Quasiprimitive Group, Bi-Quasiprimitive Group, Almost Simple Group

某类顶点拟本原和二部拟本原的3度对称图的分类
黄俊杰
云南财经大学统计与数学学院,云南 昆明

收稿日期:2019年10月9日;录用日期:2019年10月30日;发布日期:2019年11月6日

摘 要
设 是一个图, ,则称 是一个G-基图,如果G在顶点集 上是拟本原的或者二部拟本原的。在这篇文章中,我们将分类阶为 的3度对称G-基图,其中 为素数, 。
关键词 :对称图,拟本原群,二部拟本原群,几乎单群

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对于一个图 ,我们设 , 和 分别表示 的顶点集,边集和弧集, 表示 的全自同构群; 称为图 的阶。如果群 作用在 , 或 上传递,则分别称 为G-点传递图,G-边传递图或G-弧传递图。特别地,弧传递图也称为对称图。对任意的 ,定义 为点u的邻域,称 为点u的度数,记为 。如果对任意的 ,u和v的度数相等,则称 为正则图, 为图 的度数,记作 。给定一个正整数s和 上的 个点 ,称 是一条s-弧,如果 ,且 和 是邻接的。若 在 的s-弧集上传递,则称 为 -弧传递图;如果 是 -弧传递图但不是 -弧传递图,则称 为 -传递图。特别地,一个 -传递图可简单的称为s-传递图。
在代数图论中,阶数特定的对称图受到了国内外学者的广泛关注。例如:文献( [1] )给出了不大于768个点的三度图的分类。设 为素数,在文献( [2] [3] [4] )中,作者分别分类了p,2p,3p阶的对称图;之后,Praeger等在( [5] )和( [6] )中分别将其推广到pq阶的对称图。1947年,Tutte在文献( [7] )中确定了3度图的点稳定子群的结构,在此之后的几十年里,3度对称图引起了大量学者的研究,他们给出了3度对称图的各种构造方法及其分类。例如,Du和Wang在文献( [8] )中考虑了单群 上的3度Cayley图,其中r为一个素数的方幂;Feng等在( [9] )中分类了阶为8p和8p2的3度对称图;Zhou和Feng在( [10] )中对2pq阶的3度对称图进行了分类。
设 是一个传递置换群,则称X是拟本原的,如果X的每个极小正规子群都在 上传递;称X是二部拟本原的,如果X的每个极小正规子群在 上至多有两个轨道并且存在一个极小正规子群作用在 上恰有两个轨道。给定一个图 ,,称 是一个G-基图,如果G在顶点集 上是拟本原的或者二部拟本原的。研究对称图的一般分为以下两步:
第一步,研究对称图的基图;
第二步,刻画对称图的基图的正规覆盖。
基图的分类是研究对称图的基础,它不仅可以为学习对称图提供一些图例,而且对于后续研究基图的覆盖有着重要的参考作用。设 是一个阶为 的3度对称图,本文将分类 的G-基图,其中 为素数, ,,所得主要结论如下:
定理1.1:设 为素数, 是一个阶为 的3度G-基对称图,其中 ,,则 满足表1。
2. 预备知识
本文所考虑的所有图均为有限的、非空的、无向的、连通的、以及没有圈和重边的正则图。关于本文所使用的群论和图论的符号和基本概念都是标准的,可以参看学者们的著作( [11] [12] [13] [14] )等。例如:
Table 1. 3 degree G-based symmetry diagram of order 2 p m q n
表1. 阶为 的3度G-基对称图
我们用 表示n阶循环群, 和 分别表示交错群和对称群。
本节的主要内容是给出一些重要的结论和例子。首先我们给出由Tutte于1947年确定的3度对称图的点稳定子群的结构,它为我们研究3度对称图奠定了基础。
引理2.1 ( [7] ):设 是一个连通的3度 -弧传递图。则 ,并且 满足表2,其中α∈VΓ。
Table 2. Point-stabilized subgroups of 3-degree symmetry maps
表2. 3度对称图的点稳定子群
设G是一个有限群,H是G的子群。令D为H在G中的若干个形如 的双陪集之并。定义群G上关于H和D的陪集(有向)图 如下:顶点集 ,即H在G中的所有右陪集之并,边集 。陪集图有如下的性质。
引理2.2 ( [14] ):设 是群G关于H和D的陪集有向图,则
1) 是点传递图,并且 ;
2) 是连通图当且仅当 ;
3) 是无向图当且仅当 ;
4) 是G-弧传递的当且仅当 是一个单个的双陪集。
陪集图通常用于构造一些图例,下面的4个例子是根据3度图的点稳定子群的结构以及陪集图的性质构造而成,可参看文献( [1] )和( [10] )。
例2.3:1) 设 ,则G有一个子群 ,且存在一个对合x使得 ,。于是由引理2.2知陪集图 是一个阶为182的3度对称图,记为 ,且 。
2) 设
,则G有一个子群
,且存在一个对合x使得
,。于是由引理2.2知陪集图
是一个阶为182的3度对称图,记为
,且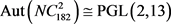 。
。
例2.4:1) 设 ,则G有一个子群 ,且存在和一个对合x使得 ,。于是由引理2.2知陪集图 是一个阶为506的3度对称图,记为 ,且 。
2) 设 ,则G有一个子群 ,且存在和一个对合x使得 且 。于是由引理2.2知陪集图 是一个阶为506的3度对称图,记为 ,且 。
例2.5:设 ,则G有一个子群 和一个对合x使得 且 。于是由引理2.2知陪集图 是一个阶为2162的3度对称图,记为 ,且其全自同构群为 。
例2.6:1) Levi图 是唯一的一个阶为30的3度对称图,它是5-正则的二部图且 。
2) Smith-Biggs图 是唯一的一个阶为102的3度对称图,且 。
3) Coxter-Frucht图 是唯一的一个阶为110的3度对称图,且 。
对于给定的较小群G,利用Magma ( [15] )软件计算包可以确定所有同构意义下的G-弧传递图。通过Magma ( [15] )直接计算,我们可得以下的5个例子。值得注意的是,在例子中所出现图,它们在同构意义下都是唯一的。
例2.7:1) 设 ,则G有一个子群 ,由Magma ( [15] )可知,存在一个阶为20的3度对称图,记为 ,且 。
2) 设
,则G有一个子群 ,于是通过Magma ( [15] )计算,存在一个阶为20的3度对称图,记为
,且
。
,于是通过Magma ( [15] )计算,存在一个阶为20的3度对称图,记为
,且
。
例2.8:设 ,则G有一个子群 或 ,于是存在两个3度对称图,分别记为 和 ,它们的阶分别为28和56,且 ,。
例2.9:设 ,则G有一个子群 或 。通过Magma ( [15] )计算可得:
1) 如果 ,则存在一个阶为28的3度对称图,记为 ,且 。
2) 如果 ,则存在两个阶为56的3度对称图,分别记为 和 ,且 ,。
例2.10:1) 设 ,则G有一个子群 ,通过Magma ( [15] )计算,存在一个阶为650的3度对称图,记为 ,且 。
2) 设 ,则G有一个子群 ,由Magma ( [15] )可知,存在一个阶为650的3度对称图,记为 ,且 。
例2.11:1) 设 ,则G有一个子群 ,存在一个阶为234的3度对称图,记为 ,且 。
2) 设 ,则G有一个子群 ,故由Magma ( [15] )计算,存在一个阶为234的3度对称图,记为 ,且 。
下面的引理是( [16],引理2.5])的一个特例,它略微改进了Praeger的结论( [17],定理4.1])。
引理2.12 ( [16] ):设
是一个连通的奇素数度的G-弧传递图,
有一个非传递的正规子群N在 上至少有两个轨道。则下面的陈述成立:
上至少有两个轨道。则下面的陈述成立:
1) N在 上半正则, , 是G/N-弧传递的,并且 是 的正规N-覆盖。
2) 是 -弧传递的当且仅当 是 -弧传递的,其中 或 。
3) ,其中 ,。
3. 定理1.1的证明
为了完整的证明定理1.1,我们先证明以下两个引理,第一个引理分类了一类单群。
引理3.1:设T是一个非交换单群且满足 ,且 ,其中 为素数, 。则下列之一成立,其中 表示 的所有素因子的个数。
1) 如果 ,则 满足表3。
Table 3. Single group T with 3 prime factors
表3. 含有3个素因子的单群T
2) 如果 ,则 满足表4。
Table 4. Single group T with 4 prime factors
表4. 含有4个素因子的单群T
证明:因为 ,所以 ,因此T满足( [18],定理I)。
如果 ,则 或3, ,因此T是一个 -群。如果 ,则 ,于是 ,故由( [18],表1)可知: 或 ,此时, 或 。如果 ,则 ,故 。再由( [18],表1)可得: ,,,,, 或 。
如果 ,由 可知 ,因此T是一个 -群,于是由( [18],定理I)可知:T满足( [18],表2)或者T同构于单群 ,其中 为一个素数的方幂。如果T满足( [18],表2),则通过检查它们的阶可得: ,此时 。如果 ,则由( [18],定理3.2和引理3.4(2),3.5(2))可知:要么 ,要么 是一个素数。
假设
,其中
是一个素数,则
。注意到, ,因此,
,因此,
即
因为 ,所以 或 ,即 或 。由此可得: ,13,17,23,31,47或97。通过检查它们对应单群 的阶可知:满足条件的q为11,13,23,31,47,97。□
假设
为素数,
是一个连通的阶为
的3度G-弧传递图,其中
,。设N是 的一个极小正规子群,则
,其中T是一个单群且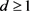 。令
。
。令
。
引理3.2:应用上面的符号说明。如果N是非交换的,则 。
证明:反证法。假设 ,则由 可知: 。如果N在 上至少有3个轨道,则由引理2.12可知,N在 上半正则,于是 ,注意到 ,矛盾。故N在 上至多有2个轨道。令 ,其中 。
假设N在 上传递。由 且 是连通图可得: 。因此, 是传递的且 是N-弧传递的。如果 在 上传递,则由( [12],定理4.2A)可知:中心化子 在 上半正则,从而 在 上半正则,这与 不能整除 相矛盾。如果 在 上至少有3个轨道,则由引理2.12可知: 在 上半正则,矛盾。因此, 在 上恰好有2个轨道,记为U和W。因为 ,故U和W构成 上的一个N-不变块系,于是 在N中的指数为2。但是, 没有指数为2的子群,矛盾。
假设N在
上恰有两个轨道,记为
。此时,
是一个二部图,其二部分别为
和
。令
。如果
作用在
上是非忠实的,则由( [19],引理5.2)可知: 是一个完全二部图,于是
,因此,
,矛盾。如果
作用在
上是忠实的,则
可以看作
上的一个传递置换群。如果
在
上传递,则由( [12],定理4.2A)可知:
在
上半正则,故
,矛盾。因此,
在
上至少有2个轨道,故由( [20],引理3.2)可知:
在
上半正则,矛盾。□
是一个完全二部图,于是
,因此,
,矛盾。如果
作用在
上是忠实的,则
可以看作
上的一个传递置换群。如果
在
上传递,则由( [12],定理4.2A)可知:
在
上半正则,故
,矛盾。因此,
在
上至少有2个轨道,故由( [20],引理3.2)可知:
在
上半正则,矛盾。□
下面给出定理1.1的完整证明。
定理1.1的证明:设 是一个连通的阶为 的3度对称G-基图,则G在 上是拟本原的或者二部拟本原的,其中 为素数, ,。设N是G的一个极小正规子群,则 ,其中T是一个单群且 。令 ,下面我们分两种情形来完成定理1.1的证明。
情形1:假设G在 上是拟本原的。
此时N在 上是传递的。如果N是一个交换群,则N在 上正则,从而 ,矛盾。因此N是非交换的,于是由引理3.2可知: ,从而 。进一步,由于 ,则 是T-弧传递的,因此 满足引理2.1,于是 。由T的传递性可得: 整除 。另一方面,由于 是T-弧传递的,则 ,于是 。故T满足引理3.1。
假设 ,则T和 满足下表5。
Table 5. Single group T with three prime factors and its corresponding ( p m , q n )
表5. 含有3个素因子的单群T及其对应的
如果 ,则 ,从而 ,故由例2.7可知 。如果 , 或 ,则 ,从而由( [10] )可知:只有当 时才存在满足条件的图 ,此时T有一个子群 。由例2.6可知 。如果 ,且 或 ,则 或3,从而由引理2.1可得, 或 。由例2.8可知 或 。如果 ,则 ,但是, 没有子群同构于 ,这与引理2.1相矛盾。如果 ,则 且 。由例2.11可知: 。
假设 ,则T和 满足下表6。
Table 6. Single group T with four prime factors and their corresponding ( p m , q n )
表6. 含有4个素因子的单群T及其对应的
如果
,其中 ,则
,由( [10] )可知,只有当
,23或47时才存在满足条件的图
,进一步,由例2.3,2.4和2.5可得,
, 或
。如果
或
,则
。但是,
和
都没有子群同构于
,这与引理2.1相矛盾。如果
或
,则
或
,此时
或
,由Magma ( [15] )计算可知,此时不存在满足条件的图
。
,则
,由( [10] )可知,只有当
,23或47时才存在满足条件的图
,进一步,由例2.3,2.4和2.5可得,
, 或
。如果
或
,则
。但是,
和
都没有子群同构于
,这与引理2.1相矛盾。如果
或
,则
或
,此时
或
,由Magma ( [15] )计算可知,此时不存在满足条件的图
。
情形2:假设G在 上是二部拟本原的。
此时,G有一个极小正规子群 在 上恰有两个轨道,分别记为 和 。于是, 是一个二部图,并且其二部分别为 和 。令 ,则 ,,。如果N是交换的,则N在 上正则,从而 ,矛盾。因此N是非交换的。由引理3.2可知: 是一个非交换单群。如果 作用在 或 上是非忠实的,则由( [19],引理5.2)可知: 是一个完全二部图,于是 。故, ,矛盾。假设 作用在 和 上是忠实的,则由( [21],定理1.5)可知下列之一成立:
(a) 在 上是拟本原的;
(b) 有两个正规子群 , 满足 且它们在 半正则。进一步,群 在 上正则。
对于情形(b),有:
,矛盾。下面考虑情形(a)。假设
在
上是拟本原的,则
有一个极小正规子群T且T是一个单群,于是由O’Nan-Scott-Praeger定理( [17] )可知:
或
。如果
,则
是全形单型,且T在
上正则。因此 ,矛盾。故
。进一步,如果T不是G的唯一极小正规子群,则由
可知
,于是G的正规子群
,矛盾。故
。进一步,如果T不是G的唯一极小正规子群,则由
可知
,于是G的正规子群 在
上有
个轨道,这与G在
上是二部拟本原的相矛盾。故,T是G的唯一极小正规子群,即G是几乎单的且其基柱
。令
,
在
上有
个轨道,这与G在
上是二部拟本原的相矛盾。故,T是G的唯一极小正规子群,即G是几乎单的且其基柱
。令
, ,其中
且
。由于
,于是由引理2.1可知
,其中
且
。由于
,于是由引理2.1可知 ,因此
整除
。另一方面,由于
,则
,。故T满足引理3.1。
,因此
整除
。另一方面,由于
,则
,。故T满足引理3.1。
假设
。此时T和
满足表5。如果
,则由Altas ( [22] )可知
。因此
,,且 ,于是由引理2.1可知,
。故由例2.7可知
。如果
,则
,于是
或
。若
,则
,于是
,由Magma ( [15] )计算可知:此时不存在满足条件的图
。若
,则
,于是
,由例2.6可知
。如果
,则
,且
或
。于是
,并且G有两个子群分别同构于
和
。故由例2.9可知:
,,或
。如果
,则由Altas ( [6] )可知
,此时与
且
相矛盾。如果
,则
,于是
,此时
,这与引理2.1相矛盾。如果
,则
,从而
,此时
,由例2.11可知
。如果
,则
,故
,此时
,但是,
不存在48阶的子群,矛盾。
,于是由引理2.1可知,
。故由例2.7可知
。如果
,则
,于是
或
。若
,则
,于是
,由Magma ( [15] )计算可知:此时不存在满足条件的图
。若
,则
,于是
,由例2.6可知
。如果
,则
,且
或
。于是
,并且G有两个子群分别同构于
和
。故由例2.9可知:
,,或
。如果
,则由Altas ( [6] )可知
,此时与
且
相矛盾。如果
,则
,于是
,此时
,这与引理2.1相矛盾。如果
,则
,从而
,此时
,由例2.11可知
。如果
,则
,故
,此时
,但是,
不存在48阶的子群,矛盾。
假设 。此时T和 满足表6。如果 , 或 ,则 ,于是 , 或 。此时, ,这与引理2.1相矛盾。如果 ,则 ,此时与 且 相矛盾。如果 或 ,则 ,于是 或 。若 ,则 ,但是,G没有子群同构于 ,这与引理2.1相矛盾。若 ,则 ,这与引理2.1相矛盾。如果 ,则 ,于是 ,,然而,G没有子群同构于 ,矛盾。如果 , 或 ,则 ,故 , 或 ,进一步可得, 或 。故由例2.3,2.4和2.6可知: , 或 。如果 ,则 ,于是 或 。因此, 或 。由例2.10可知 或 。□
基金项目
国家自然科学基金资助项目(80031010061)资助。
文章引用
黄俊杰. 某类顶点拟本原和二部拟本原的3度对称图的分类
A Classification on a Class of Vertex Quasiprimitive and Bi-Quasiprimitive Cubic Symmetric Graphs[J]. 理论数学, 2019, 09(09): 989-997. https://doi.org/10.12677/PM.2019.99125
参考文献
- 1. Conder, M.D.E. and Dobcsanyi, P. (2002) Trivalent Symmetric Graphs on up to 768 Vertices. Journal of Combinatorial Mathematics and Combinatorial Computing, 40, 41-63.
- 2. Chao, C.Y. (1971) On the Classification of Symmetric Graphs with a Prime Number of Vertices. Transactions of the American Mathematical Society, 158, 247-256. https://doi.org/10.2307/1995785
- 3. Cheng, Y. and Oxley, J. (1987) On Weakly Symmetric Graphs of Order Twice a Prime. Journal of Combinatorial Theory, Series B, 42, 196-211. https://doi.org/10.1016/0095-8956(87)90040-2
- 4. Wang, R.J. and Xu, M.Y. (1993) A Classification of Sym-metric Graphs of Order 3p. Journal of Combinatorial Theory, Series B, 58, 197-216. https://doi.org/10.1006/jctb.1993.1037
- 5. Praeger, C.E., Wang, R.J. and Xu, M.Y. (1993) Symmetric Graphs of Order a Product of Two Distinct Primes. Journal of Combinatorial Theory, Series B, 58, 299-318. https://doi.org/10.1006/jctb.1993.1046
- 6. Praeger, C.E. and Xu, M.Y. (1993) Vertex-Primitive Graphs of Order a Product of Two Distinct Primes. Journal of Combinatorial Theory, Series B, 59, 245-266. https://doi.org/10.1006/jctb.1993.1068
- 7. Tutte, W.T. (1947) A Family of Cubical Graphs. Mathematical Pro-ceedings of the Cambridge Philosophical Society, 43, 459-474. https://doi.org/10.1017/S0305004100023720
- 8. Du, S.F. and Wang, F.R. (2005) Arc-Transitive Cubic Cayley Graphs on PSL(2,p). Science in China, 48, 1927-1308.
- 9. Feng, Y.Q., Kwak, J.H. and Wang, K.S. (2005) Classifying Cubic Symmetric Graphs of Order 8p or 8p2. European Journal of Combinatorics, 26, 1033-1052. https://doi.org/10.1016/j.ejc.2004.06.015
- 10. Zhou, J.X. and Feng, Y.Q. (2010) Cubic Vertex-Transitive Graphs of Order 2pq. Journal of Graph Theory, 65, 285-302. https://doi.org/10.1002/jgt.20481
- 11. Biggs, N. (2004) Algebraic Graph Theory. Cambridge University Press, Cambridge.
- 12. Dixon, J.D. and Mortimer, B. (1997) Permu-tation Groups. Spring-Verlag, New York. https://doi.org/10.1007/978-1-4612-0731-3
- 13. 徐明曜. 有限群导引(上)[M]. 北京: 科学出版社, 1999.
- 14. 徐明曜. 有限群导引(下)[M]. 北京: 科学出版社, 1999.
- 15. Bosma, W., Cannon, J. and Playoust, C. (1997) The MAGMA Algebra System I: The User Language. Journal of Symbolic Com-putation, 24, 235-265. https://doi.org/10.1006/jsco.1996.0125
- 16. Li, C.H. and Pan, J.M. (2008) Finite 2-Arc-Transitive Abelian Cayley Graphs. European Journal of Combinatorics, 29, 148-158. https://doi.org/10.1016/j.ejc.2006.12.001
- 17. Praeger, C.E. (1992) An O’Nan-Scott Theorem for Finite Qua-siprimitive Permutation Groups and an Application to 2-Arc-Transitive Graphs. Journal of the London Mathematical Society, 47, 227-239. https://doi.org/10.1112/jlms/s2-47.2.227
- 18. Huppert, B. and Lempken, W. (2000) Simple Groups of Order Divisible by at Most Four Primes. Izvestiya Gomel’skogo Gosudarstvennogo Universiteta Im. F. Skoriny, 16, 64-75.
- 19. Giudici, M., Li, C.H. and Praeger, C.E. (2003) Analyzing Finite Locally s-Arc-Transitive Graphs. The Transactions of the American Mathematical Society, 356, 291-317. https://doi.org/10.1090/S0002-9947-03-03361-0
- 20. Lu, Z.P., Wang, C.Q. and Xu, M.Y. (2004) On Semisym-metric Cubic Graphs of Order 6p2. Science in China Series A, 47, 1-17.
- 21. Li, C.H., Praeger, C.E., Venkatesh, A. and Zhou, S.M. (2014) Finite Locally-Quasiprimitive Graphs. Algebra Colloquium, 21, 627-634. https://doi.org/10.1142/S1005386714000571
- 22. Conway, J.H., Curtis, R.T., Norton, S.P., Parker, R.A. and Wilson, R.A. (1985) Atlas of Finite Groups. Oxford University Press, London/New York.
