ABSTRACT

By constructing the general solution of differential equations or complementing function value. We obtain the singular solutions of a class of differential equations and correct the errors in solving the singular equations of these differential equations in other books and literatures.

Keywords:Envelope, Singular Solutions, C-Discriminant, C-Discriminant Curve, Constructing the General Solution

一类微分方程奇解的另一种求法

孔志宏

太原师范学院数学系，山西 晋中

收稿日期：2020年2月1日；录用日期：2020年2月20日；发布日期：2020年2月27日

摘 要

通过构造微分方程通解的方法，求得一类微分方程的奇解，纠正了其它书籍、文献在求这些微分方程奇解过程中的错误( [1] 除外)。

关键词 :包络，奇解，C-判别式，C-判别曲线，构造通解

Copyright © 2020 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

根据解的存在唯一性定理 [2]，如果微分方程

中右端函数在某区域G上连续，在G上有界或连续，则在G内初值问题的解是存在且唯一的，

从而在G内肯定不存在奇解。如果存在唯一性定理的条件不在整个的定义域内成立，则奇解(如

果存在的话)只有到那些破坏了存在唯一性定理条件的点集中去找，也就是到使得无界的点集中去找。

对于某些微分方程，如，等，它们的奇解(包络)是存在的。但是用c-判别曲线法求通解曲线族的包络时，由于通解是在的取值有一定限制的条件下求得的，所以根据c-判别式求得的c-判别曲线与通解是矛盾的，到目前为止，凡是涉及到求诸如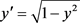，之类的微分方程的包络(奇解)问题的书籍、文献(如 [3]、 [4]、 [5] )等，都是在这样的矛盾情形下，逻辑不自洽地“指导出”微分方程的奇解(包络)。结论是正确的，但求解过程是逻辑矛盾的。

本文通过构造通解法解决了这个矛盾。此前笔者曾通过补充定义法解决了这个矛盾(见 [1] )。

2. 构造通解法

例1判断微分方程

(1)

是否存在奇解，如果存在就求出来。

解右端函数，它在带形区域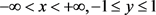：上定义、连续。

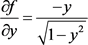
当时无界，所以方程(1)如果有奇解，只能是，显然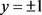是(1)的两个特解。下面求方程(1)的通解。

当时(注意这个限制条件)，(1)可改写为

,

积分得

,

于是

(2)

其中c为任意常数。由于也是(1)的解，故也可把(1)的通解表示为

或

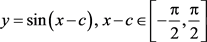(3)

其中C为任意常数。

现在求通解曲线族(3)的包络。这里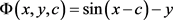，，c-判别式为

c-判别曲线为

, 与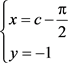

这两条c-判别曲线均为有，，满足非蜕化条件，故两条c-判别曲线都是通解曲线族(3)的包络，从而都是方程(1)的奇解。

例2 [6] 判断微分方程

(4)

是否存在奇解，如果存在就求出来。

解右端函数在其定义域内是连续的。

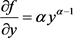
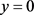当时无界，所以方程(4)如果有奇解，只能是，显然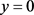是(4)的一个特解。下面求(4)的通解。

当时(注意这个限制条件)，(4)可改写为

,

积分得

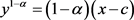,或,

或

,或 (5)

其中c为任意常数。由于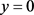也是(4)的解，故也可把(4)的通解表示为

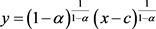, (6)

易得c-判别曲线为

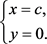
同样易知为通解曲线族(6)的包络，从而是(4)的奇解。

文章引用

孔志宏. 一类微分方程奇解的另一种求法
Another Solution Method of Singular Solutions of a Class of Differential Equations[J]. 理论数学, 2020, 10(03): 139-142. https://doi.org/10.12677/PM.2020.103020

参考文献