ABSTRACT

The process of deriving the particle’s equations of motion in the space-time with torsion can be formulated as the following four steps: first, writing the Lagrangian of matter field and gravitational field for the physical system; second, calculating the energy-momentum tensor density of matter field; third, writing the particle’s momentum, and using the Dirac delta function, the relations between energy-momentum tensor density of the matter field and its particle’s momentum can be found; fourth, considering the Lagrangian symmetry and conservation law of the physical system the relations among energy-momentum tensor density and generalized spin density, and space-time curvature, and torsion can be found. From this relation, the equations of motion for the particle in the space-time with torsion can be derived. In order to clarify some people’s misunderstanding of the equations of motion for particles in space-time with torsion, we mainly explain the theoretical basis of the above four steps in this article. And this paper will also show that the particle’s equations of motion in general relativity are the special case of particle’s equations of motion in torsional gravity, and the particle’s equations of motion in the special relativity are the special case of particle’s equations of motion in general relativity.

Keywords:Lagrangian, Matter Field, Gravitational Field, Equations of Motion, Curvature, Torsion, Energy-Momentum Tensor Density, Generalized Spin Density

有挠时空理论中质点运动方程研究

陈方培

大连理工大学物理与光电技术学院，辽宁 大连

Email: chenfap@dlut.edu.cn

收稿日期：2015年6月20日；录用日期：2015年7月2日；发布日期：2015年7月9日

摘 要

在有挠时空中推导质点运动方程的过程可归结为下述四步骤：一、写出物理体系的物质场拉氏量和引力场拉氏量；二、计算物质场的能动张量密度；三、写出质点的4维动量，利用狄拉克δ函数的特性，可找到该物质体系物质场的能动张量密度与质点的4维动量的关系；四、考虑拉氏量的对称性和守恒律，以获得物质场的能动张量密度、广义自旋密度和时空曲率、挠率的关系。由此关系即可导出有挠时空中质点运动方程。为了澄清当前一些人对有挠时空中质点运动方程的一些误解，本文将着重讲解上述四步骤的理论基础。本文还将说明，广义相对论中的质点运动方程是有挠引力理论中的质点运动方程的特殊情况，狭义相对论中的质点运动方程是广义相对论中的质点运动方程的特殊情况。

关键词 :拉氏量，物质场，引力场，质点运动方程，曲率，挠率，能动张量密度，广义自旋密度

1. 引言

本文所要讨论的时空是4维时空，因之一个质点在时空的位置须由1个时间坐标和3个空间坐标，即由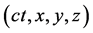或来确定。当质点在时空中运动时，它的时空位置连续发生变化，一般来说，该质点在时空中的轨迹为一条4维曲线。这条曲线常可用微分方程来表示，在物理学中称这个微分方程为质点运动方程。在物理学中常常要推导各种情况下的质点运动方程；必须强调，质点运动方程与质点所在时空有关。

大致来说，时空的不同可由曲率和挠率的不同来区分。狭义相对论的时空为曲率为0和挠率为0的时空，广义相对论的时空为曲率不为0但挠率为0的时空，有挠时空是曲率和挠率均不为0的时空[1] 。本文将说明，广义相对论中的质点运动方程是有挠引力理论中的质点运动方程的特殊情况，狭义相对论中的质点运动方程是广义相对论中的质点运动方程的特殊情况。

在物理学的各门理论中，质点运动方程均可由最小作用量原理[1]

(1)

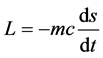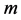导出。在狭义相对论和广义相对论的一些文献中，常把式(1)中质点的拉氏量取作，式中的为

运动质点的质量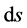，为运动质点所经过的元间隔，于是式(1)可化为

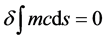(2)

在狭义相对论中，须满足

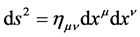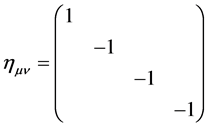， (3)

在广义相对论中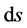，须满足

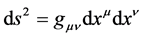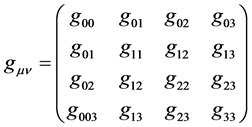， (4)

注意，最多只有10个独立变量。将式(3)或式(4)代入式(2)，就可分别导得狭义相对论和广义相对论中的质点运动方程[2] ：

(5)

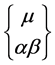对于狭义相对论，常可使化为零，而对于广义相对论，一般来说不为零。按照微分几何的看法[3] ，由式(2)所导出的4维曲线式(5)是极值线，常被称为短程线。

由于式(2)和式(5)在狭义相对论中和广义相对论中都成立，常使得一些初学引力理论的读者，甚至还有少数相对论教科书的作者误认为式(2)、式(5)对于质点在任意时空(包括有挠时空在内)之中的运动都能适用。本文要强调指出，这种看法是错误的。读者阅读本文后就可得知：式(2)和式(5)不适用于有挠时空，在有挠时空中质点运动方程不是短程线。

在引力理论中对质点运动方程的推导和讨论是个难点，对其理解容易出现错误，加以研究有挠时空及其引力理论要用到一些近代数学，使初学者常感到困难。为了解决这些困难，本文将从引力理论的基本概念和基本规律[1] [4] [5] 出发来推导有挠时空中的质点运动方程，并着重说明于一般情况下，在有挠时空引力理论中推导质点运动方程所依据的一些理论基础。这些说明概括了对有挠引力理论、广义相对论与狭义相对论中的质点运动方程的推导。

2. 有挠时空中质点运动方程的推导及其理论基础

在有挠时空中推导质点运动方程的过程可归结为下述四步骤：一、写出物理体系的拉氏量并把其分成物质场拉氏量和引力场拉氏量；二、选用合适的定义，求出物质场的能动张量密度；三、在一定条件下可把物质场视为质点，写出质点的4维动量，利用狄拉克δ函数[6] 的特性，可找到该物质体系物质场的能动张量密度与质点的4维动量的关系；四、考虑拉氏量的对称性和守恒律，可获得物质场的能动张量密度、广义自旋密度和时空曲率、挠率的关系；由此关系可求得有挠时空中质点运动方程和广义自旋运动方程[5] 。下面我们就按上述步骤来导出有挠时空中质点运动方程。我们将着重讲解推导的理论基础。

2.1. 物理体系的物质场拉氏量和引力场拉氏量

我们先从拉氏函数讲起。在物理理论中常用拉格伦日函数(简称拉氏量)来描述物理体系，拉氏量包含了它所描述之物理体系的许多信息，物理体系的场方程、各种守恒量和守恒定律都可由拉氏量及其对称性导出。存在万有引力现象之物理体系的总拉氏量，一般来说，可分成三部分[1] ：

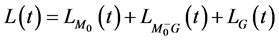(6)

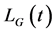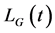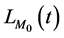是纯物质拉氏量，它包括物质之间无相互作用时对拉氏量的贡献以及物质与物质之间、除引力之外的其它基本相互作用(即电磁、强、弱相互作用)对拉氏量的贡献。是纯引力场拉氏量，是物质与引力场之间相互作用的拉氏量。这里要注意，不要把纯引力场的拉氏量包含在或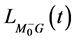之中。这是因为用来表达引力场场量的度规、联络既反映时空的特性，又表达了引力场的强弱；而纯物质场只通过质量、能量和动量来反映物质本身的特性但不反映时空的特性。这使得纯物质场与纯引力场是有区别的，不能混淆在一起。纯引力场同物质与引力之间的相互作用场也是有区别的，也不能混淆在一起。

在式(6)中若用表示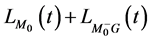，则式(6)将表示为

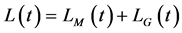(6’)

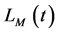被称为物质的综合拉氏量。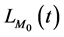只是物质场量的泛函(泛函是函数的函数)，而是物质场量和引力场量的泛函。本文认为引力理论在实质上是引力规范场理论，若采用Kibble对引力规范场理论的研究方法[7] ，可得到

(7)

(8)

上面两式中[1] ，表示物质场，表示标架场，表示标架联络场。标架场和标架联络场分别从不同角度反映了时空同引力场的特性，它们都是引力场场量。式(7)明显表明:物质的综合拉氏量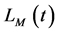是物质场场量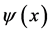和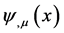、标架场场量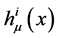以及标架联络场场量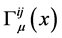的泛函；纯引力场拉氏量与物质场场量无关，只是标架场场量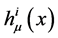和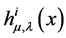、以及标架联络场场量和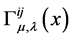的泛函。曲率和挠率是由标架场和标架联络场所决定的。

2.2. 物质场的能动张量密度

有了拉氏量就可以推导质点的运动方程[5] [7] 。质点的运动方程理应反映时空和质点运动的特性。在理论物理中，时空和质点运动的特性可由能动张量密度来反映。能动张量密度乃是力学中能量、动量概念的高度推广[6] 。本文将从能动张量密度着手推导在有挠时空中质点的运动方程。

为了解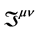，我们先把式(1)推广为4维形式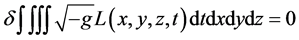[1] ：

(1’)

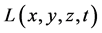为度规张量行列式的开方根。在式(1’)中的出现，是由于作用量是标量，而拉氏量为标量，又在坐标变换下，

，可以保证作用量是标量。令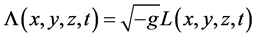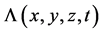，称为拉氏量密度[1] [6] [7] 。因与式(1)比较，式(1’)中的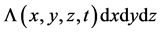相当于式(1)中的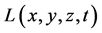，故被称为拉氏量密度。

在引力理论中，对物质场能动张量密度，存在两类定义：

其一，定义物质场能动张量密度为

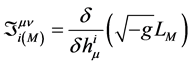
(或为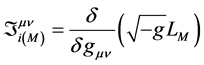)，式中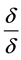是变分求导的符号。

其二，定义物质场能动张量密度为

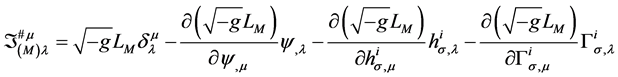
文献[1] 论证了并推导出这两类定义之间的关系。关于这两类定义的对比、分析、讨论及其应用我们将写另文讨论。

2.3. 利用狄拉克δ函数的特性，建立物质场的能动张量密度与其质点的4维动量的关系

物质的存在有两种形式，一种为以粒子(或质点)的形式存在，另一种为以场的形式存在。在牛顿力学中，常可把物质看成以质点的形式存在，任何大型物体都总可看成是由一群质点(或质点系)组成的。在场论中，原则上是把物质看成是物质场，但在讨论物质场受力运动时，或者研究物质场的量子化时，又常把物质看成以质点或一群粒子的形式存在。这时往往把同一物质既看成是场，也看成是质点或一群粒子。

本文将采用文献[6] 的观点，在文献[6] 中认为同一物质的物质场的能动张量密度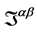与其所对应的质点动量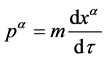可由下述关系相联系[6] ：

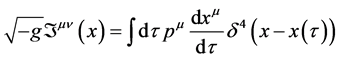(9)

在式(9)左边物质的能动张量密度，是按照物质以场的形式存在计算出来的，上式右边物质质点的动量是按照物质以质点的形式存在计算出来的。式(9)利用了狄拉克delta函数[6] 的特性。

当某物质体系既可视为场也可视为质点时，按照物质以场的形式存在计算的结果与按照物质以质点的形式存在计算的结果应当是一致的，这就是文献[6] 假定式(9)可以成立的根据。另一方面，文献[6] 认为质点的4维动量与其能动张量的分量密切相关，这如同认为电荷的电量是其4维电流的0分量。

在式(7)中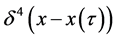是4维delta函数，它满足

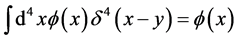(10)

(11)

因此，可按关系

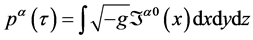(12)

来算出质点的4维动量。这是推导质点运动方程很关键的一步。为了避免讲解比较复杂的张量密度，文献[5] 中只引用了式(12)，而未说明其来源，文献[1] 更未介绍式(12)及质点运动方程；都易使读者对这些概念模糊不清，甚至出现错误的理解，故本文对此作了上述详细的说明。

2.4. 有挠时空中质点运动方程的导出

根据有挠时空的特点及认定物质场具有Poincare’群局部变换不变性(即在Poincare’群局部变换下，若物质场的综合拉氏量之作用量的变分恒为0，可求得物质场的能动张量密度满足下述关系[5] )：

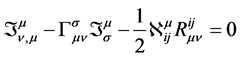(13)

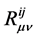式(13)中，为物质场的能动张量密度，为时空的曲率张量，

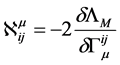为物质场的广义自旋张量密度。在文献[5] 中，对式(13)的来源有详细的说明，本文就不重复了。

利用式(12)即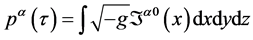及与其类似的关系[5]

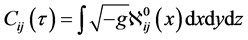
(式中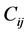表示质点或粒子的广义自旋)，再运用微分几何计算，可由式(13)导出

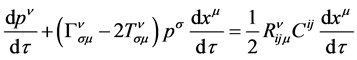(14)

这就是有挠时空中质点的运动方程。式中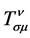为时空挠率，它的两个下标是反对称的。

3. 广义相对论是有挠引力理论的特殊情况；狭义相对论是广义相对论的特殊情况

关于广义相对论可视为有挠引力理论之特殊情况以及狭义相对论可视为广义相对论之特殊情况的看法，在文献[1] 和[8] 中已做过详细讨论，本文不再多讲；有问题的读者请参考这两篇文献。在此我们只是强调指出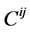，是质点或粒子的广义自旋角动量，按照定义，在广义相对论中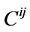恒等于0 [5] [8] 。又对于广义相对论，挠率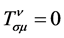，于是式(14)化为

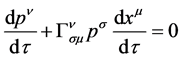(15)

这表明了广义相对论中的质点运动方程是有挠引力理论中的质点运动方程的特殊情况。对于狭义相对论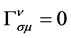， [1] ，于是式(15)化为

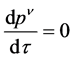(16)

这表明了狭义相对论的质点运动方程是广义相对论中的质点运动方程的特殊情况。

4. 结束语

为了澄清对有挠时空中质点运动方程的一些误解，本文着重介绍了在有挠时空中推导质点运动方程的四个步骤及其理论基础，并进一步说明了广义相对论中的质点运动方程是有挠时空引力理论中的质点运动方程的特殊情况，狭义相对论中的质点运动方程是广义相对论中的质点运动方程的特殊情况。对有挠时空中质点运动方程的一些误解往往是由于对狭义相对论、广义相对论和有挠时空引力理论之间的关系和区别缺乏理解而产生的。对这些关系和区别有了理解，误解就容易消去，这便是写作本文的主要目的。

文章引用

陈方培, (2015) 有挠时空理论中质点运动方程研究
The Study on Particle’s Equations of Motion in the Space-Time with Torsion. 现代物理,04,73-78. doi: 10.12677/MP.2015.54010

参考文献 (References)