Modern Physics
Vol.07 No.02(2017), Article ID:19890,7
pages
10.12677/MP.2017.72004
Theory of the Heat Generation in Giant Magnetoresistance Model
Xiaoxue Zhang
Beijing Technology and Business University, Beijing

Received: Feb. 24th, 2017; accepted: Mar. 12th, 2017; published: Mar. 15th, 2017

ABSTRACT
Spin caloritronics is a newly-explored research field concerning mainly the interaction of spin and heat, and has attracted extensive research interests recently. Heat generation in magnetic multilayers is a serious problem, because it has significant effects on the electric, thermal, and magnetic properties of nanoscale electronic devices. Here we study theoretically the heat generation due to spin transport in magnetic multilayers by using a macroscopic approach based on the Boltzmann equation. There exists extra heat generation due to spin accumulation besides the nominal Joule heat, when a current flows through the magnetic multilayers. On the basis of the giant magnetoresistance (GMR) model, we derived the expressions for the distribution of heat generation. We also compared the distribution and magnitude of the heat generation in antiparallel (AP) and parallel (P) alignments. Our analysis shows that the AP alignment leads to larger heat generation than the P alignment. Therefore, the heat generation in the structure changes dramatically with the relative alignment of the two ferromagnetic layers, which is similar to the GMR effect.
Keywords:Giant Magnetoresistance Model, Spin-Dependent Heat Generation, Antiparallel Configuration, Parallel Configuration
巨磁阻模型中热产生分布的理论研究
张小雪
北京工商大学,北京
收稿日期:2017年2月24日;录用日期:2017年3月12日;发布日期:2017年3月15日

摘 要
自旋热效应是最近出现的研究领域,内容围绕于自旋与热流的相互作用,引起了广泛的讨论。由于热效应对纳米尺度的电子器件的电学、热学和磁学性能的研究有重要的意义,磁性多层结构中存在的热产生是一个不容忽视的问题。我们用基于玻尔兹曼方程的宏观近似,在理论上研究了磁性多层结构中由于输运导致热产生。在磁性多层结构中通入电流后,除了会产生普通材料的焦耳热外,还存在来自于自旋积累的额外热产生。我们用巨磁阻模型计算了热产生分布的表达式,并比较了反平行结构和平行结构中自旋相关热产生分布和大小的差异。分析结果表明,在反平行结构中,自旋相关热产生比较多,对材料的影响比较大,而平行结构中自旋相关热产生比较少。所以,当两个铁磁层磁化方向变化时,装置中的热产生也发生明显的变化,是一种类巨磁阻效应。
关键词 :巨磁阻模型,自旋相关热产生,反平行结构,平行结构

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自旋电子学是将电子自旋和电荷输运相结合的学科,在凝聚态物理中扮演着重要角色。1988年,磁性多层结构中的巨磁阻效应被发现,为通过磁场对自旋作用有效控制电子运动提供了方法 [1] [2] 。巨磁阻效应实际应用于读取磁头信息,这为磁记录信息存储密度的飞速发展做出了很大的贡献,从此磁性多层结构在实验和理论研究中被广泛使用。最近,热电效应和自旋电子学的联系引发了研究人员的热烈讨论,所以出现了一个研究分支叫做自旋热效应 [3] 。当存在温度梯度时,磁性层中的自旋电子的分布会发生变化,产生电势差,这种效应叫做自旋相关塞贝克效应 [4] 。由于热电效应在磁性器件中扮演重要角色,磁性多层结构中的热产生也应受到重视。
近些年,一些实验结果也表明,在自旋电子器件中如果存在热产生,可能会对的基本特性造成影响 [5] [6] 。2010年,Bakker等人在实验上证明了热产生对横向自旋阀基本电阻的作用确实是存在的,引起了基本阻值的显著增加 [7] 。2012年,Erekhinsky等人研究了在横向自旋阀中器件自身产生的焦耳热对自旋注入的影响 [8] 。除了以上实验,还有一些实验结果证实了热产生对磁性多层的影响 [9] [10] [11] ,说明在磁性器件中的热产生是不可忽视的,热产生的研究对以自旋为基础的器件有重要意义。但是以上研究考虑的焦耳热均仅来自普通材料电阻,并未考虑自旋积累产生的额外热产生,由于热效应在器件中的重要性,对自旋积累部分导致的额外热产生的计算是需要被探讨的问题。
在理论方面,对磁性多层结构中的热产生研究也取得了一些进展 [12] [13] ,有理论计算表明,当没有电荷流,仅存在纯自旋流的情况,依然有能量损耗,即热产生 [14] [15] [16] 。基于上述的原因,我们应该意识到磁性多层结构中热产生的分布和大小,对准确研究器件中的各项特性有很重要的意义。本文的目的是通过理论计算得到巨磁阻结构中热产生分布的表达式,对分布情况进行研究,以及分析,这些工作对其他理论结果的精确性和实验数据的准确拟合都有帮助。
在本文中,我们将以产生巨磁阻效应的装置为模型,给出一个更简明的热产生分布表达式。并且运用该表达式计算了反平行结构和平行结构中的热产生分布,通过代入具体材料参数作图分析,我们发现在两种结构中,自旋相关热产生的分布有很大的差异。
2. 热产生分布表达式的简化
在这部分,我们将磁性多层结构中热产生分布的表达式进行变形,得到一个更简洁的表达形式。我们的计算是用巨磁阻模型为基础,巨磁阻模型在磁学领域中是常用的研究模型,最基本的巨磁阻模型是由两个铁磁层和一个非磁层组成的三明治结构,两个铁磁层被非磁层分隔开 [2] 。当两个铁磁层的磁化方向相反时,称为反平行结构,磁化方向相同时称为平行结构。这种磁性多层器件的电阻大小与两个铁磁层的磁化方向密切相关,反平行结构的电阻明显大于平行结构,这种现象叫做巨磁阻效应。
在下面的计算中,我们把非磁层的中心位置作为z轴,非磁层为有限厚度,左右铁磁层与非磁层的界面位置分别在 和
和 ,两个铁磁层的材料相同且为半无限层。在反平行结构(antiparallel configuration(中,对于左边的铁磁层(FM1)磁化方向是“向上”的,右边的铁磁层(FM2)是“向下”的。在平行结构(paraller configuration)中,两个铁磁层的磁化方向都是“向上”。在巨磁阻模型中 [2] ,电流密度
,两个铁磁层的材料相同且为半无限层。在反平行结构(antiparallel configuration(中,对于左边的铁磁层(FM1)磁化方向是“向上”的,右边的铁磁层(FM2)是“向下”的。在平行结构(paraller configuration)中,两个铁磁层的磁化方向都是“向上”。在巨磁阻模型中 [2] ,电流密度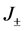 和电化学势
和电化学势 满足以下宏观输运方程
满足以下宏观输运方程
 (1)
(1)
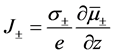 (2)
(2)
其中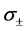 和
和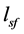 表示电导率和自旋扩散长度,等式(1)是和自旋积累相关的,等式(2)代表欧姆定律。我们将电流密度和电化学势分为常数项和指数项,分别代表体(bulk)部分和自旋相关(spin-dependent)部分
表示电导率和自旋扩散长度,等式(1)是和自旋积累相关的,等式(2)代表欧姆定律。我们将电流密度和电化学势分为常数项和指数项,分别代表体(bulk)部分和自旋相关(spin-dependent)部分
 (3)
(3)
 (4)
(4)
在巨磁阻模型的各层中,常数项和指数项满足下列关系 [2]
 (5)
(5)
 (6)
(6)
Tulapurkar等人用玻尔兹曼输运方程计算了自旋流产生的能量损耗 [14] ,给出了单位时间内热产生密度随位置变化的表达式。稳态时,单位时间内的热产生密度为
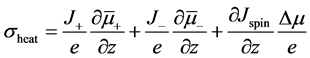 (7)
(7)
其中自旋流为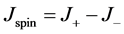 ,与自旋积累相关的项
,与自旋积累相关的项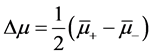 。将等式(2)、(5)和(6)代入上式,得到热产生分布更简洁的表达形式
。将等式(2)、(5)和(6)代入上式,得到热产生分布更简洁的表达形式
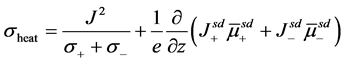 (8)
(8)
从等式(8)我们可以看出,磁性多层中的热产生来自于体材料和自旋相关两部分。我们将单位时间内热产生密度改写成这种更简洁的形式,方便接下来的计算。等式(8)中的第一项为普通材料的热产生,即焦耳热,在铁磁层中的值为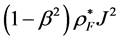 ,
,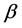 为体不对称参数,在非磁层中的值为
为体不对称参数,在非磁层中的值为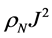 。等式(8)的第二项为由于自旋积累导致的热产生,我们将这部分记为
。等式(8)的第二项为由于自旋积累导致的热产生,我们将这部分记为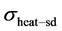 。
。
通过等式(8)可以看出,在磁性多层结构中,热产生普遍存在,那么由于热产生对器件造成的影响也是不可避免的。一方面,在磁性多层结构中热产生的分布如果随位置变化,则会出现温度梯度,那么由于自旋相关塞贝克效应等机制,将会出现自旋积累分布的变化进而形成电势差。另一方面,实验上已经证明,仅考虑器件中的普通焦耳热,就会引起器件基本参数的变化,所以自旋相关部分的额外热产生对器件的影响也是不容忽视的。
3. 两种结构中自旋相关热产生的比较
在这部分我们只对自旋积累部分的热产生进行讨论,在反平行结构和平行结构两种情况下,研究自旋相关热产生分布情况的表达式,并且通过运用真实材料的参数,进行作图分析。需要注意的是,为了计算简便以及图像清楚,我们并没有考虑界面电阻的存在。
将自旋相关部分自旋流和电化学势的表达式(参见 [2] )代入等式(8),我们得到自旋相关热产生的分布。我们定义几个电阻,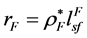 ,
,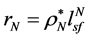 ,
,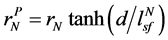 ,
,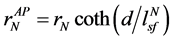 。在铁磁层中(
。在铁磁层中( 或
或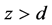 ),单位时间内的热产生密度随位置变化的表达式为
),单位时间内的热产生密度随位置变化的表达式为
 (9)
(9)
其中“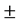 ”分别代表左右两侧的铁磁层,而系数的定义为
”分别代表左右两侧的铁磁层,而系数的定义为
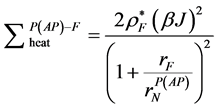 (10)
(10)
在非磁层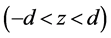 中,单位时间内的热产生密度随位置变化的表达式为
中,单位时间内的热产生密度随位置变化的表达式为
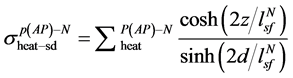 (11)
(11)
其中系数为
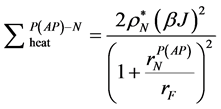 (12)
(12)
从铁磁层和非磁层的自旋相关热产生表达式(9)和(11)可以看出,自旋相关热产生的分布是随位置变化的,从界面处向两侧扩散,特征长度为自旋扩散长度的一半。同时,系数的表达式(10)和(12)表明,自旋相关热产生的大小不仅与自身材料的阻值相关,也与相邻层的材料各项参数有紧密的联系。所以,我们有必要通过图像量化地分析各层自旋相关热产生的分布,接下来将代入材料的具体参数进行模拟。
3.1. 反平行结构
在这个部分,我们用真实的材料参数来模拟反平行结构的自旋相关热产生分布情况。铁磁层FM1 和FM2选择金属Co,材料的相关参数为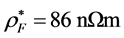 ,
,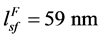 ,
,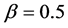 ,非磁层N选择金属Cu,厚度设为
,非磁层N选择金属Cu,厚度设为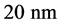 ,材料的相关参数为
,材料的相关参数为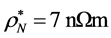 ,
,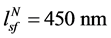 。我们将这些参数代入等式(9)、(10)、(11)和(12)中,得到图1。
。我们将这些参数代入等式(9)、(10)、(11)和(12)中,得到图1。
在图1中,我们可以看出,在反平行结构中,铁磁层的自旋相关热产生较多,与铁磁层普通材料热产生的比在看靠近界面处可以达到0.6,说明在巨磁阻模型中由于自旋积累导致的热产生不应该被忽略。
自旋积累对铁磁层热产生的贡献比较明显,但对非磁层影响较小。一般情况下,在器件中通入电流后,铁磁体由于自身材料的电阻比较大,产生的焦耳热大于非磁体。在巨磁阻模型中,存在自旋积累,反平行结构中铁磁层的自旋相关热产生也是大于非磁层的,这无疑会增大相邻两层的热量差值,造成更明显的温度梯度。当磁性多层结构中存在不可忽略的温度梯度时,一些相关的热效应或者其他机制将会出现,并且可能改变器件的基本特性。
3.2. 平行结构
在这部分,我们用同样的材料参数模拟平行结构的自旋相关热产生分布情况,不同之处为,非磁层厚度我们选取两种情况,分别为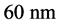 和
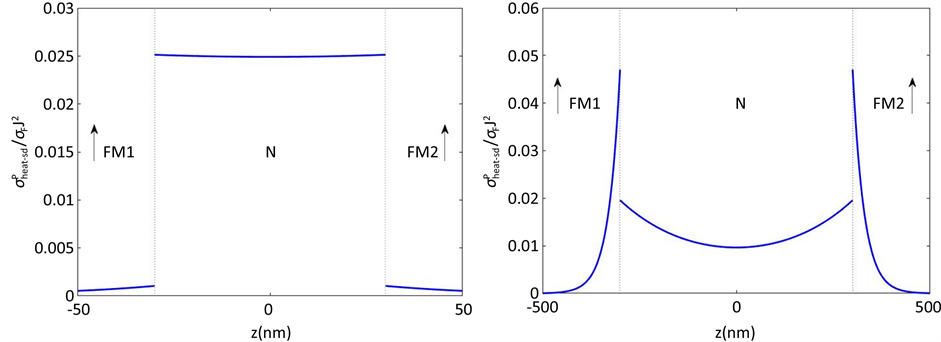
和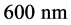 。当非磁层厚度较小时,如图2(a),界面附近的自旋相关热产生在非磁层甚至可以比铁磁层更多。当非磁层厚度较大时,情况与上述相反,如图2(b)。这种差异的存在是取决于参数的,并不需要太多关注。但这也表明,自旋相关热产生可以对相邻两层的热量差
。当非磁层厚度较小时,如图2(a),界面附近的自旋相关热产生在非磁层甚至可以比铁磁层更多。当非磁层厚度较大时,情况与上述相反,如图2(b)。这种差异的存在是取决于参数的,并不需要太多关注。但这也表明,自旋相关热产生可以对相邻两层的热量差
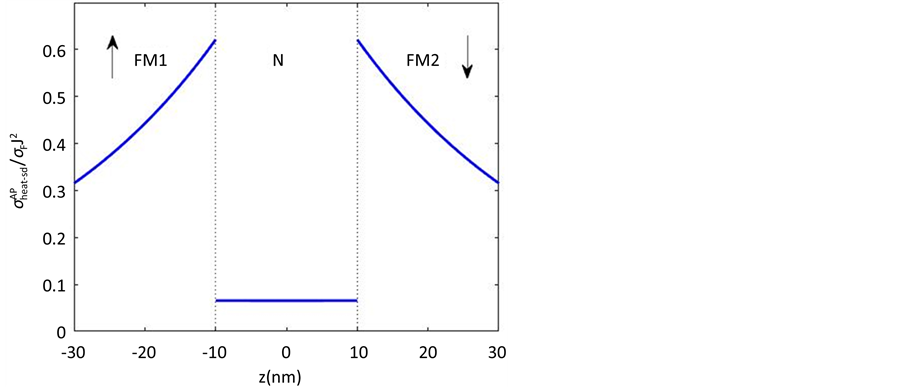
Figure 1. Spin-dependent heat generation per unit time in antiparallel configuration
图1. 反平行结构单位时间内自旋相关热产生密度的分布
 (a) (b)
(a) (b)
Figure 2. Spin-dependent heat generation per unit time in parallel configuration. The thickness of nonmagnetic layer is (a) 60 nm, (b) 600 nm
图2. 平行结构单位时间内自旋相关热产生密度的分布,非磁层厚度为(a) 60 nm,(b) 600 nm
值有负影响,并不总是增大热量差值。
同时,我们可以看出,与反平行结构相比,在平行结构中,自旋相关热产生较少,与反平行结构约差一个数量级,如图2(a)。在平行结构中,左右两侧铁磁层的磁化方向一致,在界面处的自旋积累较少,那么等式(8)中自旋相关的电流密度和电化学势的值比较小,所以自旋相关热产生较少。所以,在平行结构中,额外热产生几乎可以忽略。
比较两种结构的自旋相关热产生,我们发现反平行情况和平行情况有明显的差别,这是由于两种结构的电流密度和电化学势的分布差别也很大,在反平行结构中的自旋积累较多,在平行结构中的自旋积累较少 [2] 。在巨磁阻模型中,通过外加磁场改变铁磁层的磁化方向时,热产生也随之发生变化,这是一种类巨磁阻效应。但是,由于温度变化速度较慢,这种现象并不能通过测量明显的呈现出来。
4. 结论
自旋电子学是一门正在发展的学科,实验、理论与应用均表明自旋电子学有着广泛研究前景。近年来对自旋热效应的研究,展示出温度在自旋电子学中扮演着不可忽视的角色。在自旋电子器件中,自旋输运过程中产生的热量损耗对器件许多方面的性能有显著影响。所以,对磁性多层结构热产生的研究是需要被关注的问题,这对精确得到器件中的各类数据以及器件应用的限制条件有重要意义。
巨磁阻模型是磁学领域的经典模型,我们在巨磁阻模型中通过公式推导和图像分析得出了一些结论。我们通过铁磁层和非磁层中自旋相关热产生的表达式可以看出,热产生的分布并不是处处相同,而是与位置相关的,从界面处以特征长度向两侧扩散。这种特点意味着在巨磁阻模型中由于热量分布不均匀,将会存在温度梯度,进而可能引起器件中发生一些热效应,以及影响器件的基本参数。在理论研究和实验探索方面,我们应该考虑到这些效应的影响,使用更恰当的参数。各层的自旋相关热产生的大小不仅依赖于该层的材料参数,也与相邻层的材料参数密切相关。那么,在选择实验材料时,我们也应该考虑到材料参数对整体器件的影响,以便获得适当的实验数据。
我们在反平行结构和平行结构两种情况下用实际材料的参数作图,发现反平行结构的铁磁层中自旋相关热产生较多,与普通材料热产生相比也很可观,而平行结构中自旋相关热产生较少,几乎可以忽略。当巨磁阻模型中铁磁层磁化方向为反平行时,通入电流后,器件中的热产生来自于两部分,即体材料的焦耳热和自旋相关热产生,且这两部分的热产生在铁磁层中的数值都大于非磁层,那么自旋积累将使铁磁层与非磁层中的热量差值增大,器件中由于温度梯度导致的热效应也会更加明显。但遗憾的是,这些理论结果并不能用当今的实验手段给出佐证。最后,反平行结构和平行结构中热产生的情况差异很大,说明器件中的热产生与两个铁磁层的磁化方向密切相关,所以我们称这种现象是一种类巨磁阻效应。当实验中的器件出现这种类巨磁阻效应时,两类结构的热产生的差异会使器件受到不同程度的热效应影响,进而对两类结构各类参数造成影响。如果在实验操作和实际应用中考虑这种效应的存在,将会对设计出更合理的实验方案有一定的帮助。
通过对巨磁阻模型的热产生进行计算和分析,我们可以更清晰的了解巨磁阻模型中各层热产生的情况,也为今后更准确获得器件运行时的材料参数提供了帮助。
基金项目
北京工商大学研究生科研能力提升计划项目。
文章引用
张小雪. 巨磁阻模型中热产生分布的理论研究
Theory of the Heat Generation in Giant Magnetoresistance Model[J]. 现代物理, 2017, 07(02): 25-31. http://dx.doi.org/10.12677/MP.2017.72004
参考文献 (References)
- 1. Baibich, M.N., Broto, J.M., Fert, A., et al. (1988) Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Physical Review Letters, 61, 2472-2475. https://doi.org/10.1103/PhysRevLett.61.2472
- 2. Valet, T. and Fert, A. (1993) Theory of the Perpendicular Magnetiresistance in Magnetic Multilayers. Physical Review B, 48, 7099-7113. https://doi.org/10.1103/PhysRevB.48.7099
- 3. Bauer, G.E., Saitoh, E. and van Wees, B.J. (2012) Spin Caloritronics. Nature Materals, 11, 391-399. https://doi.org/10.1038/nmat3301
- 4. Uchida, K., Takahashi, S., Harii, K., et al. (2008) Observation of the Spin Seebeck Effect. Nature, 455, 778-781. https://doi.org/10.1038/nature07321
- 5. Mu, C., Hu, S., Wang, J., et al. (2013) Thermo-Electric Effect in a Nano-Sized Crossed Permalloy/Cu Junction under High Bias Current. Applied Physics Letters, 103, Article ID: 132408. https://doi.org/10.1063/1.4822330
- 6. Dejene, F.K., Flipse, J. and van Wees, B.J. (2014) Verification of the Thomson-Onsager Reciprocity Relation for Spin Caloritronics. Physical Review B, 90, Article ID: 180402. https://doi.org/10.1103/PhysRevB.90.180402
- 7. Bakker, F.L., Slachter, A., Adam, J.P., et al. (2010) Interplay of Peltier and Seebeck Effects in Nanoscale Nonlocal Spin Valves. Physical Review Letters, 105, Article ID: 136601. https://doi.org/10.1103/PhysRevLett.105.136601
- 8. Erekhinsky, M., Casanova, F.I., Schuller, I.K., et al. (2012) Spin-Dependent Seebeck Effect in Non-Local Spin Valve Devices. Applied Physics Letters, 100, Article ID: 212401. https://doi.org/10.1063/1.4717752
- 9. Krause, S., Herzog, G., Schlenhoff, A., et al. (2011) Joule Heating and Spin-Transfer Torque Investigated on the Atomic Scale Using a Spin-Polarized Scanning Tunneling Microscope. Physical Review Letters, 107, Article ID: 186601. https://doi.org/10.1103/PhysRevLett.107.186601
- 10. Jeon, K.R., Min, B.C., Park, S.Y., et al. (2013) Thermal Spin Injection and Accumulation in CoFe/MgO Tunnel Contacts to n-Type Si through Seebeck Spin Tunneling. Applied Physics Letters, 103, Article ID: 142401. https://doi.org/10.1063/1.4823540
- 11. Dankert, A. and Dash, S.P. (2013) Thermal Creation of Electron Spin Polarization in n-Type Silicon. Applied Physics Letters, 103, Article ID: 242405. https://doi.org/10.1063/1.4845295
- 12. Foros, J., Brataas, A., Bauer, G.E., et al. (2009) Noise and Dissipation in Magnetoelectronic Nanostructures. Physical Review B, 79, Article ID: 214407. https://doi.org/10.1103/PhysRevB.79.214407
- 13. Léonard, F. (2011) Reduced Joule Heating in Nanowires. Applied Physics Letters, 98, Article ID: 103101. https://doi.org/10.1063/1.3561772
- 14. Tulapurkar, A.A. and Suzuki, Y. (2011) Boltzmann Approach to Dissipation Produced by a Spin-Polarized Current. Physical Review B, 83, Article ID: 012401. https://doi.org/10.1103/PhysRevB.83.012401
- 15. Taniguchi, T. and Saslow, W.M. (2014) Dissipation Due to Pure Spin-Current Generated by Spin Pumping. Physical Review B, 90, Article ID: 214407. https://doi.org/10.1103/PhysRevB.90.214407
- 16. Taniguchi, T. and Saslow, W.M. (2016) Heat Production by Diffusion of Pure Spin Current. Journal of Magnetism and Magnetic Materials, 400, 168-170. https://doi.org/10.1016/j.jmmm.2015.07.041