ABSTRACT

In this paper, the relationship between the multifragmentation and chaotic dynamics in low energy nuclear reactions and heavy ion collisions at intermediate energy is briefly reviewed. After recalling some concepts about the compound nuclear reaction model and the random matrix theory, we introduce the properties of excited nuclear matter in the spatial-temporal evolution process, such as spinodal instability, phase transition, which are closely related to the nonlinear dynamics. Some important nonlinear dynamical characteristics in these processes are summarized qualitatively. Moreover, the strange structure of the excited nuclear matter at the sub-densities has also been surveyed briefly.

Keywords:Low and Intermediate Energy, Nuclear Reaction, Multifragmentation, Nonlinear Dynamics, Chaos

中低能核反应中的混沌与多重碎裂的非线性动力学机制

邢永忠，方玉田

天水师范学院基础物理研究所，甘肃 天水

收稿日期：2020年2月27日；录用日期：2020年3月17日；发布日期：2020年3月24日

摘 要

本文对低能核反应和中重离子碰撞中的多重碎裂现象与混沌动力学之间的联系进行了简要的综述。主要定性地介绍和总结了目前人们在对原子核反应的研究过程中所揭示出的非线性动力学特征。文中首先简介了复合核反应模型与随机矩阵理论预言的一致性。随后回顾了受激核物质系统的不稳定性、相变等与非线性动力学密切相关的基本特征。最后介绍了近年来人们以分子动力学方法为基础，所揭示出的受激核物质的不稳定性与低密核物质的奇异结构。

关键词 :中低能，核反应，多重碎裂，非线性动力学，混沌

Copyright © 2020 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

几十年来，人们通过对原子核反应的研究，已经对核物质在不同条件下的相互作用规律有了比较深入的认识 [1] [2] [3] [4]。然而，由于重离子碰撞是一个极端复杂的量子多体过程，其中不仅涉及到核物质相互作用在极端条件下的具体表现形式，而且涉及到强相互作用下多体系统的平衡与驰豫等问题。因此，长期以来，人们从动力学和统计学等多个角度对重离子碰撞进行了大量的探索研究，虽然已经成功地解释了碰撞中所出现的许多重要现象并揭示出了其本质规律。但是，就目前现状来看，人们还远没有彻底清楚决定重离子碰撞动力学过程的全部因素。譬如，中能碰撞中原子核的多重碎裂现象及其产生的动力学机制等问题，仍是需要人们继续探讨的重要课题。从时空演化的角度来看，中能重离子核反应是一个经历压缩、膨胀、碎裂或衰变的复杂动力学过程，碰撞动力学本身既有确定论的因素，又有随机性因素。因此，既需要人们分别从动力学和统计学两个不同的角度来认识这一过程，同时，还需要揭示两者间的相互联系。实际上，上世纪70年代发展起来的非线性科学，即混沌学，被认为是架起确定论动力学与随机性统计学之间的桥梁 [5]。因此，揭示多重碎裂的动力学原因与统计学结果之间的联系，不仅有利于人们对核反应过程的深刻认识，而且，还可以深化人们对因果律等基本规律的理解 [6]。

混沌运动的典型表现为非线性动力学的时空演化对于初始条件的敏感性，其本质在于：确定论的动力学系统产生的随机性。确定论的非线性动力学方程的演化结果与随机矩阵理论预言的一致性，被认为是混沌的量子表现或量子混沌的典型特征 [7]，亦被认为是判断一个量子体系是否存在混沌运动的标准 [8]。近年来，人们从随机矩阵理论出发，对于原子核结构和核反应的部分特征做出了很好的解释。因此，本文在简要介绍了复合核反应模型与随机矩阵理论预言的一致性之后，介绍了碰撞核系统的不稳定性、相变、分岔等与非线性动力学密切相关的典型特征，最后介绍了近年来人们以分子动力学方法为基础，所揭示出来的碰撞核物质的不稳定性与低密核物质的奇异结构等现象。其目的在于：力图明确重离子核反应与混沌动力学之间的联系，明确重离子核反应过程中的非线性特征，揭示其动力学机制，探讨通过非线性动力学方法来解释重离子核反应及其多重碎裂现象的可能性。

2. 复合核反应模型与随机矩阵理论

诞生于上世纪50年代的随机矩阵理论(RMT)正是Wigner [8] [9] 等人在研究原子核的复合核反应过程 [10] 中发展起来的。如果入射粒子和原子核发生碰撞形成一个复合系统，这个系统存在的时间大大超过粒子穿过核所用的时间而不衰变，则这个系统被称为复合核。玻尔假设：复合核一经形成，它的衰变由自身的性质(寿命、能量、角动量和宇称等)完全决定，而与它形成的历史无关。入射能量在核子的发射阈值附近的核反应(几个MeV的数量级)，由于准束缚态或库仑势垒的存在，其激发函数出现共振，根据共振峰的数目，可以将复合核反应按三种不同状况来处理，即孤立能级共振，当入射粒子能量接近于复合系统的某一能级时，截面出现独立的共振峰，此时，可以用Breit-Wigner公式描写。当几个共振能级相互重叠而无法区分，但仍然可以观测到截面随入射粒子能量而发生涨落时，可以通过对涨落的分析提取到重叠能级的有关知识。不论是独立的共振峰还是相互重叠的共振峰，峰间距与宽度的分布均表现出统计随机性。当众多能级被激发，涨落由于统计平均而不甚明显时，需要用统计理论描述。然而，Ericson曾指出 [11]：随着复合系统中间态的增多，截面随入射能量的变化并非趋于平滑，而是继续涨落——随机性将会进一步增强。这些特征告诉人们随机性的产生有着更为深刻的物理涵义。

定义能谱中相邻能级之间的间距为紧邻能级间距，可以用紧邻能级间距与平均能级间隔之间的差来反应能级间距的涨落。理论和实验均已证明 [12]，这个涨落与一个实对称矩阵所描述的哈密顿系统的相邻本征值之差具有相同的统计性质，即：紧邻能级间距满足Wigner分布

$P\left(s\right)=\frac{\pi s}{2}\exp \left(-\frac{\pi s^2}{4}\right)$ (1)

其中，s是紧邻能级间距。实对称哈密顿矩阵的矩阵元 $\left\{H_{\mu \nu },\mu ,\nu =1,2,3,\cdots \right\}$ 为平均值为零、且关联函数满足：

$\langle H_{\mu \nu }{H}_{\rho \sigma }\rangle =\frac{{\lambda }^2}{N}\left({\delta }_{\mu \rho }{\delta }_{\nu \sigma }+{\delta }_{\mu \sigma }{\delta }_{\nu \rho }\right)$ (2)

的高斯随机数。这样的哈密顿系统组成的系综，称之为高斯正交系综(GOE)。研究表明这样的哈密顿系统所对应的经典运动会表现出强的混沌特征。(1)式也就是截面激发函数中的相邻共振峰之距的涨落。共振峰的半宽度满足所谓的Porter-Thomas分布

$P_{\nu }\left(x\right)\text{d}x=\frac{\nu }{2\Gamma \left(\frac{\nu }{2}\right)}{\left(\frac{\nu x}{2}\right)}^{\frac{\nu -2}{2}}\exp \left(-\frac{\nu x}{2}\right)\text{d}x$ (3)

其中 $\nu =1$。系综的本征值之间的关联用统计量 ${\Delta }_3$，称之为谱刚度来描述。对于遵循GOE统计的能谱，在能谱区间范围 $L>15$ 的情况下，其平均刚度为：

${\bar{\Delta }}_3\left(L\right)\approx \frac{1}{{\pi }^2}\left(\ln L-0.0687\right)$ (4)

按照统计理论 [13] [14]，复合核反应截面可以用S矩阵来表示： ${\sigma }_{ab}=\frac{\pi }{k_a^2}{g}_a{\left|{\delta }_{ab}-S_{ab}\right|}^2$，其中 $S_{ab}$ 就是

由入射道a到出射道b的S矩阵。反应截面对能量的平均值可以写作 $\langle {\sigma }_{ab}\rangle =\langle {\sigma }_{ab}^{SE}\rangle +\langle {\sigma }_{ab}^{CN}\rangle$。对于形状弹性(形状非弹性 $a\ne b$ )散射，其截面为

${\sigma }_{ab}^{SE}=\frac{\pi }{k_a^2}{g}_a{\left|{\delta }_{ab}-\langle S_{ab}\rangle \right|}^2$

复合核反应截面为

${\sigma }_{ab}^{CN}=\frac{\pi }{k_a^2}{g}_a\langle {\left|S_{ab}^{fl}\right|}^2\rangle$ (4)

在 $\langle S_{ab}\rangle ={\delta }_{ab}\langle S_{aa}\rangle$ 的条件下，定义穿透系数 $T_a=1-{\left|\langle S_{aa}\rangle \right|}^2$，按照Hauser-Fechbach理论，并考虑到宽度涨落修正后，复合核反应截面为

${\sigma }_{ab}^{CN}=\frac{\pi }{k_a^2}{g}_a\frac{T_a{T}_b}{{\displaystyle \underset{c}{\sum }{T}_c}}{W}_{ab}$ (5)

其中 $W_{ab}$ 为宽度涨落修正因子。由此可见，核反应截面的确定可归结为计算S矩阵。目前，有多种方法计算 ${\sigma }_{ab}^{CN}$。近年来，文献 [10] 的研究表明：利用Hauser-Beshbach投影算符方法，可以直接建立起复合核反应与随机矩阵理论(GOE)的联系。

定义P和Q分别为开道和闭道投影算符，将碰撞系统的Hamiltonian写为：

$\left(E-H_{PP}\right)P\psi =H_{PQ}Q\psi$ (6)

$\left(E-H_{QQ}\right)Q\psi =H_{QP}P\psi$ (7)

定义闭道空间的等效哈密顿量为

$H_{QQ}^{Eff}=H_{QQ}+H_{QP}\frac{1}{E^{+}-H_{PP}}{H}_{PQ}$ (8)

消去开道空间波函数后，得

$S_{ab}=S_{ab}^{\left(0\right)}-2\pi i\langle {\psi }_a^{(-)}|H_{PQ}\frac{1}{E^{+}-H_{QQ}^{Eff}}{H}_{QP}|{\psi }_b^{(+)}\rangle$ (9)

在 $S_{ab}^{\left(0\right)}$ 的本征空间S矩阵元可写为

$S_{ab}={\delta }_{ab}^{\left(0\right)}-2\pi i\langle {\psi }_a|H_{PQ}\frac{1}{E-H_{QQ}^{Eff}}{H}_{QP}|{\psi }_b\rangle$ (10)

其中状态： $|{\psi }_a^{(+)}\rangle$ 满足 $\left(E-H_{PP}\right)|{\psi }_a^{(+)}\rangle =0$，且 $|{\psi }_a\rangle =\exp \left\{-i\varphi \right\}|{\psi }_a^{(+)}\rangle$。设 $\left\{|\mu \rangle \right\}$ 是闭道空间的正交归一基矢，且 $W_{\mu a}=\langle \mu |H_{QP}|{\psi }_a\rangle =W_{a\mu }=W_{\mu a}^{*}$，$H_{\mu \nu }=\langle \mu |H_{QQ}|\nu \rangle$，则：

$S_{ab}={\delta }_{ab}-2\pi i{\displaystyle \underset{\mu \nu }{\sum }{W}_{a\mu }{\left(D^{-1}\right)}_{\mu \nu }{W}_{\nu b}}$ (11)

$D_{\mu \nu }=E{\delta }_{\mu \nu }-H_{\mu \nu }+i\pi {\displaystyle \underset{c}{\sum }{W}_{\mu c}{W}_{c\nu }}$ (12)

将上式中描述系统的等效哈密顿量 $H_{\mu \nu }^{eff}$ 换成 $H_{\mu \nu }^{GO\text{E}}$ 矩阵，即将其矩阵元用相互独立的、满足Gaussian分布的随机变量。则(11)和(12)两式变为

$S_{ab}^{\left(GOE\right)}={\delta }_{ab}-2\pi i{\displaystyle \underset{\mu \nu }{\sum }{W}_{a\mu }{\left(D^{-1}\right)}_{\mu \nu }{W}_{\nu b}}$ (13)

$D_{\mu \nu }=E{\delta }_{\mu \nu }-H_{\mu \nu }^{\left(GOE\right)}+i\pi {\displaystyle \underset{c}{\sum }{W}_{\mu c}{W}_{c\nu }}$ (14)

这里，矩阵 $H^{GOE}$ 的矩阵元之间必须满足：

$\langle \langle H_{\mu \nu }^{GOE}\rangle \rangle =0$ (15)

$\langle \langle H_{\mu \nu }^{GOE}{H}_{\rho \sigma }^{GOE}\rangle \rangle =\frac{{\lambda }^2}{N}\left({\delta }_{\mu \rho }{\delta }_{\nu \sigma }+{\delta }_{\mu \sigma }{\delta }_{\nu \rho }\right)$ (16)

这里我们用双引号表示对系综的平均，利用文献 [15] 所提出的三重积分公式和Monte-Carlo数值方法，可以确定出其中的参数 $\lambda$ ： $d=\frac{\pi \lambda }{N}$。同时，由于 $H_{\mu \nu }^{GO\text{E}}$ 的正交不变性，可通过正交变换使

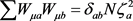，定义 $x_a=\frac{{\pi }^2{\zeta }_a^2}{d}$，则

${\bar{S}}_{aa}=\frac{1-x_a}{1+x_a}$，$T_a=\frac{4x_a}{{\left(1+x_a\right)}^2}$ (17)

在数值计算中，可令G为 $N\times \Lambda$ 的矩阵，O为一正交矩阵，要求 $O^{-1}{G}^{\text{T}}GO=diag\left({\zeta }_a^2\right)$，其中 $\Lambda$ 为开道的数目，N为矩阵 $H^{GOE}$ 的维数，这样可确定参数 $\zeta$ 并取 $W=GO$。

按照上述GOE理论，结合文献 [15] 提出的多重积分公式和Monte-Carlo方法可以计算低能的散射矩阵和平均截面、预言中子阈能(或质子的库仑势垒)附近的共振与随机行为间的关系，并对其统计性质进行分析，不仅可以正确地预言共振峰之间的间距和复合核衰变的宽度分布，而且还可以正确计算散射角分布等问题，也可以给出共振峰的个数N与数据误差之间的关系。当然，无法利用统计理论预言单个共振的位置与宽度。实际上，建立具有动力学基础的复合核反应理论是人们多年来追求的目标。直到1980年代，受到人们对量子混沌研究的启发，逐步建立起了RMT和复合核反应间的联系，亦即，出现了量子混沌散射的概念。首次将混沌系统的能谱特征与RMT联系起来的为 [16]，而第一个将复合核散射、量子混沌等与RMT联系起来的为文献 [17]。

3. 碰撞核体系的不稳定性与多重碎裂的动力学机制

对于发生碰撞的两原子核所产生的碰撞核物质，在其激发能较低时，将通过发射核子而退激发，当激发能较高时，终态除了不同质量的碎块外，大部分为单个核子。但在中间激发能的情形下，中等质量碎块(IMF)的数目最多，热力学理论研究表明：此时正好对应着碰撞系统处于气体和液体共存的状态 [18]。实际上，核相互作用力与气体分子范德瓦尔斯力的相似性，启发人们将相变的概念引入到重离子碰撞过程中。碰撞系统的碎裂过程，可以与热力学系统的稳定与不稳定性以及相变等物理过程密切地联系起来。由热力学理论出发，可以明确地给出由热力学宏观量所表达的一级和二级相变的具体条件 [19]。在基于平均场的研究中，引入单体分布函数的涨落之后，通常利用线性响应理论将决定涨落时空演化的Vlasov方程线性化而得到不同波矢所决定的不同模式(Mode)的色散关系，并按照色散关系的本征值在复数空间的取值来定义激发核物质的稳定性 [20]。文献 [21] 借助Viriald定理，建立了单个核子的经典运动与系统的温度、压强等宏观物理量之间的联系，并由此证实在Skyrme-Type相互作用下，由哈密顿动力学方程所描述的单个核子在相空间演化的经典方程所决定的系统，其不稳定区域与热力学方法所定义的不稳定区是完全一致的。

Morawetz [22] 在平均场的基础上，从动力学的角度建立了相变与局域不稳定性之间的密切联系，明确了表面起主导作用的不稳定性与发生在Fermi能附近的体积支配的Spinodal不稳定性之间的区别与关系。Peilert et al. [23] 利用经典动力学方法也证实了由于Spinodal不稳定性而导致低密核物质的结团(clustering)现象的出现，这一过程明显依赖于核物质的状态方程。这些研究告诉我们一个共同的结论：碰撞过程中出现的不稳定区域,是导致系统解体的动力学根源，处于这些不稳定区域的核物质在非线性平均场的作用下不断演化，最终导致碰撞系统的解体，是中能重离子碰撞中多重碎裂的一个重要机制。

为了明确碎裂与碰撞系统平衡的关系，文献 [24] 利用量子分子动力学模型(QMD)，对Xe + Sn在入射能量为50 A MeV的反应过程进行了模拟，并与实验结果(INDRA data)进行了比较。分析发现：反应终态中观察到的碎块，大多都是在200 fm/c时从碰撞系统中飞离出来的，其横动能基本上决定于核子的Fermi能量。那么，碎块在飞离系统时为什么没有受到周围物质的作用而遭受破坏？文献 [24] 借助渗透模型的思想，即用Lattice模型对此作了如下解释：将两个发生碰撞的原子核，看作是两个格栅(Lattices)，每个格栅的Site被一个核子所占据，Site的数目等于原子核中的核子数目。原子核的碰撞就相当于两个格栅的相互穿越，在此中弹核中的核子与靶核中的核子之间发生直接碰撞，碰撞几率由核子间的碰撞截面所决定，对于直接发生碰撞的两核子，由于发生了动量的转移，一个格栅中的核子可能被击出而留下一个空穴。当出现足够多的空穴时(但不能过多)，这个格栅就会分裂成碎块。核子间的碰撞几率越大，则空穴的数目就越多，产生的碎块质量就越小，反之，若碰撞少，空穴数就少，人们观察到的就只有类弹或类靶碎块。这样的模型似乎告诉我们：多重碎裂是非平衡过程中出现的瞬时动力学后果。然而，其他的观察物理量与上述统计模型的一致性，包括与RMT理论，又预示着碎裂是碰撞系统平衡后的现象，到底如何，至今仍然没有确定的答案。

4. 核物质的不稳定性与混沌特征

一般说来，混沌是非线性动力学系统时空演化的特殊表现形式。在两原子核碰撞过程中，核物质的时空演化出现非线性性和不稳定性，为混沌运动创造了必然条件。所以，寻求核碰撞过程中的混沌及其表现，自然是人们追求的目标之一。文献 [25] 对于中能重离子碰撞过程的分析表明：碰撞过程实际上由线性和非线性动力学共同支配，在碰撞的开始阶段，可以用线性响应理论来描述，但随着扰动强度的增大，非线性性明显增强，系统逐渐显示出块状结构(Lumpy)，经过足够长时间的演化后，系统进入气体与液体共存状态，碎块逐渐增大，其过程主要由非线性动力学所支配 [26]。

人们已经对经典非线性动力学和混沌有了比较清楚的研究，明确了一系列刻画非线性动力学中混沌运动特征的物理量。然而，对于量子混沌，虽然试图在量子力学框架内定义可积与不可积等概念 [27]，但目前比较公认的做法仍是通过量子经典对应来确定量子系统的可积性 [28]。因此，描述经典非线性动力学中混沌运动的物理量，诸如彭加蒙截面、李亚普洛夫指数、关联函数等均是定量衡量量子系统运动是否具有混沌的特征物理量。另一方面，正如前所述，目前人们对重离子碰撞这样的量子多体过程的研究，主要采用半经典的数值方法，这正好为人们研究碰撞动力学的混沌表现提供了便利。因此，人们已经将单体相空间分布函数随时空的演化作为基本计算对象(如Vlasov、BUU)，深入研究了平均场动力学的时空演化行为，详细计算了诸如李亚普洛夫指数、关联函数，分形维数，广义熵等通常用以判断和标志经典混沌的各种物理量 [29] [30] [31]。计算结果清楚地显示：非线性平均场的时空演化，出现明显的强混沌特征，这一特征被看作是导致碰撞系统多重碎裂的根本原因。譬如：2000年，王楠 [32] 和马玉刚 [33] 等分别利用量子分子动力学模型对真实原子核碰撞的模拟，计算出了系统演化过程中的最大李亚普洛夫指数和信息熵,并清楚地显示出了相变、多重碎裂以及混沌机制的共存。

孤立波是非线性科学中的重要概念之一，是非线性动力学方程的一种定域行波解,在物理上看作为非线性激发的、能量不弥散的稳定的准粒子或孤立子，单个原子核或碎块可以看作为孤立子，文献 [34] 的研究指出，在受激核物质演化碰撞过程中，由于决定系统体积不稳定性的非线性项与决定着表面不稳定性的色散项之间的相互干涉，可以导致孤立子波的形成，亦即可以形成碎块。

实际上，主要用于研究中能原子核碰撞的不同动力学理论模型，均可以对碰撞系统的稳定与不稳定性以及相变的发生给出了明确的判断。对于建立在平均场基础之上，描述单体分布函数时空演化的输运模型，如Vlasov方程、时间有关的Hartree-Fock (TDHF)、相对论平均场方法和BUU输运模型等，虽然没有足够地计入核子间的关联，并且通过求平均效应来处理核子的演化与核子间的碰撞(BUU模型中)，但仍然可以给出处于稳定与不稳定区域的“平均轨道”在时空演化过程中的差别，其具体表现请见文献 [21] [35] [36] [37]。

以Boltzmann方程为基础并计入残余相互作用涨落的Boltzmann-Longevin (BL)模型，被认为是能够揭示研究反应动力学过程中随机性的有力工具，此模型可以更加清楚地描述涨落在系统的时空演化过程中的具体表现及其所导致后果。人们通过采用不同的方法(Lattice方法、相格点方法，或试验粒子方法等)来求解BL方程，细致地揭示出了碰撞系统演化的各种非线性动力学特征。特别是，最近提出的Boltzmann-Longevin One Body (BLOB)方法 [38]，可以清楚地显示出碰撞系统演化过程中的轨道分岔等典型的混沌特征。

5. 低密度下，受激核物质的演化与空间分布的奇异结构

量子分子动力学模型(QMD)是从描述系统的哈密顿量出发，通过时间有关的变分方法得到核子的演化方程，并用相干态波包来表示核子，波包的数目与原子核中的核子数目一一对应。因而充分地计及了关联效应 [39]，特别适合于研究中能重离子碰撞的多重碎裂。这类方法的另一个特点在于不仅可用于研究平衡与非平衡系统的演化，而且不需要对核结构做出任何假设 [23]。近年来，人们应用分子动力学方法研究了受激核物质的演化和形状相变特征，从微观动力学的角度解释了核物质在特定条件下演化时其空间结构的变化：对于低密核物质，在系统随密度的变化过程中会出现球形、圆柱、厚块、以及空心柱和空心球等形状，称之为pasta结构。这以现象，对于人们理解超新星和中子星的形成与演化起到了很大的帮助作用。因此，引起了核物理及天体物理领域研究人员的极大兴趣。

早在1997年，T. Maruyama等 [40] 就对QMD方法进行了恰当的改进和推广，将核子在平均场中的演化方程变成了含阻尼项的哈密顿方程，

${\stackrel{\dot{}}{R}}_i=\frac{\partial H}{\partial P_i}-{\mu }_R\frac{\partial H}{\partial R_i},{\stackrel{\dot{}}{P}}_i=\frac{\partial H}{\partial R_i}-{\mu }_P\frac{\partial H}{\partial P_i}$ (18)

其中，H是描述系统的哈密顿量，包含有Pauli势和动量相关作用势，和 ${\mu }_P$ 是阻尼系数。由此半经典动力学方程出发，可以确定出系统的能量最低态，计算发现在低密情形下，当系统在达到能量最低状态时，核物质变得不稳定并进而出现空间分布的不均匀性。在QMD模型和公式(18)的基础上，文献 [41] 考虑适当的电子背景(即质子与电子间的库仑相互作用)并引入等效温度，从动力学的角度进一步证实了均匀受激核物质在冷却过程中，可以出现一系列复杂的奇特结构并最终形成块状和柱状形状，这时，核物质的表面能与库仑能之间达到了局域平衡，演化过程的关联函数和闵可夫斯基函数可以给出这些奇异结构的定量特征，具体形式请参阅本文相关文献。

本文中我们从介绍随机矩阵理论的起源—复合核反应模型出发，总结了目前判断量子系统是否存在混沌运动比较公认的“基本判据”(涨落是否与随机矩阵理论的预言一致)。同时，介绍了随机矩阵理论在解释核反应模型的最新进展 [15]。随后，介绍了重离子碰撞过程中激发核系统所表现出来的力学不稳定、分布密度的涨落，以及涨落在非线性动力学演化过程中的放大，相变和碎裂等一系列与非线性动力学密切相关的基本过程，清晰地显示出了多重碎裂的非线性动力学机制。最后，我们对人们研究多重碎裂的微观动力学方法——分子动力学方法——在研究核物质和天体物体的演化方面所取得的最新进展做了简要介绍。由于在这一方法中，均匀的初始系统仅在平均场的作用下演化(存在阻尼)而无外在随机性的影响，最终给出了奇异的Pasta结构，由此很好的解释了中子星等天体的演化与结构。这一现象无疑与耗散系统中的出现奇怪吸引子的机制相类似。这些事实启发我们：从非线性动力学的角度来研究复杂的核反应过程对于核物理和非线性科学均具有十分重要的意义，揭示重离子碰撞的动力学机制是核物理学家和非线性物理学家的共同课题。

基金项目

本文由国家自然科学基金项目(No. 11665019)资助。

文章引用

邢永忠,方玉田. 中低能核反应中的混沌与多重碎裂的非线性动力学机制
Chaos in Heavy-Ion Collisions at Intermediate Energy and Nonlinear Dynamics of Multifragmentation[J]. 现代物理, 2020, 10(02): 7-15. https://doi.org/10.12677/MP.2020.102002

参考文献