Modern Physics
Vol.
11
No.
01
(
2021
), Article ID:
39653
,
8
pages
10.12677/MP.2021.111001
磁场作用下Oldroyd-B流体的非稳态驻点流动
白羽1,2*,王清1,2,张艳1,2
1北京建筑大学,北京
2建筑结构与环境修复功能材料北京市重点实验室,北京
收稿日期:2020年10月19日;录用日期:2020年12月28日;发布日期:2021年1月5日

摘要
本文研究了拉伸板上Oldroyd-B流体的非稳态驻点流动,此外,还考虑了磁场对流动的影响。利用合适的相似变换将控制方程转化为常微分方程。结合双参数变形展开方法与基函数方法(DPTEM-BF)求得微分方程的近似解析解。通过图形展示了各物性参数对速度场的影响,值得注意的是:随着松弛时间参数的增加,流体的粘性力增大使得流体流动阻力增强,这导致了流体流速减小;延迟时间参数的变化使得速度场增大,并且动量边界层厚度变厚;较大的磁场参数对应于较大的洛伦兹力,这个力阻碍了流体流动,因而流体流动速度降低。
关键词
Oldroyd-B流体,非稳态驻点流动,磁场,DPTEM-BF方法

Unsteady Stagnation-Point Flow of Oldroyd-B Fluid along a Stretching Sheet with Magnetic Field
Yu Bai1,2*, Qing Wang1,2, Yan Zhang1,2
1Beijing University of Civil Engineering and Architecture, Beijing
2Beijing Key Laboratory of Functional Materials for Building Structure and Environment Remediation, Beijing

Received: Oct. 19th, 2020; accepted: Dec. 28th, 2020; published: Jan. 5th, 2021

ABSTRACT
This paper examines the influence of magnetic field on unsteady stagnation-point flow of Oldroyd-B fluid towards a stretching sheet. Suitable similarity transformations are put into use to yield the ordinary differential equation, which are dealt with double-parameter transformation expansion method with base function method (DPTEM-BF). Impacts of various physical parameters on the velocity field are explored via graphs. It is noteworthy that as relaxation time parameter enlarges, the viscous force of fluid increases, which causes larger resistance to fluid flow. The increase of retardation time parameter increases both the velocity and momentum boundary layer thickness. Larger magnetic parameter corresponds to the larger Lorentz force, which impedes fluid flow and thus slows it down.
Keywords:Oldroyd-B Fluid, Unsteady Stagnation-Point Flow, Magnetic Field, DPTEM-BF Method

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,由于非牛顿流体在工业、食品以及日常生活中的广泛应用而备受研究人员的关注,如石油、油漆、淀粉液、蛋清、果浆等都是非牛顿流体。其中,Oldroyd-B流体就是常见的一种非牛顿流体,它不仅能够反映流体的松弛特性,还能表征延迟特性对流体的影响。Khan等 [1] 研究了Oldroyd-B流体流动问题。Hayat等 [2] 对多孔拉伸板上Oldroyd-B流体的混合自然流动进行了讨论。Ullah等 [3] 得到了两同轴圆柱之间Oldroyd-B流体旋转流动的精确解。此外,Alshomrani等 [4] 还探索了在分层机制作用下,热辐射和化学反应对Oldroyd-B纳米流体流动和传热的影响。Hayat等 [5] 在Alshomrani等人的基础之上还考虑了热产生/吸收的影响并且推导了其关系式。Hafeez等 [6] 采用Cattaneo-Christov双扩散模型分析了多孔旋转圆盘上Oldroyd-B流体的流动、传热和传质,并且得到了数值解。
驻点流动在熔融纺丝工艺、拉丝、玻璃吹制、金属和聚合物挤出等应用中起着至关重要的作用,因此不少学者都对驻点流动问题进行了研究。Mustafa等 [7] 研究了幂律流体的驻点流动。Sharma等 [8] 对具有二阶速度滑移的拉伸板上微极流体的驻点流动进行了分析。在布朗运动和热泳扩散存在下,Bai等 [9] 对拉伸板上Maxwell纳米磁流体的驻点流动也进行了讨论。在此基础之上,Bai等 [10] 还采用Cattaneo-Christov双扩散模型探索了具有化学反应和热辐射效应的上随体Oldroyd-B纳米磁流体的驻点流动和传热。上述学者都只研究了稳态驻点流动,但实际上流体的流动与时间也有关,以下研究人员对不同流体的非稳态驻点流动也进行了分析。Hayat等 [11] 讨论了拉伸板上二级流体的非稳态驻点流动问题。Zaib等 [12] 研究了速度滑移和热泳效应对微极流体非稳态驻点流动的影响。Awais等 [13] 还分析了在焦耳加热下,径向拉伸圆盘上Maxwell磁流体的非稳态驻点流动。Mahdy [14] 对具有Biot数效应的加热拉伸板上Oldroyd-B纳米流体的非稳态驻点流动进行了建模,并且还考虑了纳米流体的动态粘度和导热率的影响。此外,Hayat等 [15] 也对Oldroyd-B纳米流体的非稳态驻点流动问题进行了探索,并且将热产生/吸收、非线性热辐射、布朗运动以及热泳扩散的影响考虑在内。
磁流体由于同时具有独特的磁性以及流动性在扬声器、阻尼器和选矿分离等方面有着独特的价值,这一特性使得不少学者对存在磁场情况下的流体的流动问题进行了深入思考。Asghar等 [16] 得到了在磁场作用下粘性流体的库埃特流动的解析解。Hayat等 [17] 研究了倾斜磁场对指数拉伸板上三级流体流动的影响。Mabood等 [18] 对在磁场和加热作用下,拉伸板上Jeffery流体的非稳态流动问题进行了讨论,并且还考虑了变导热系数的影响。Jakati等 [19] 分析了在斜向外磁场作用下,非均匀热源/散热器、布朗运动和热泳对线性拉伸板板上Maxwell纳米流体流动的影响。此外,Hashmi等 [20] 还研究了磁场对两个无限等温拉伸盘间Oldroyd-B纳米流体的混合对流以及轴对称流动的影响。然而,很少有学者研究了磁场对Oldroyd-B流体非稳态驻点流动的影响。
本文主要研究了在磁场作用下,拉伸板上Oldroyd-B流体的非稳态驻点流动。采用合适的相似变换将偏微分方程转化为常微分方程,并且使用双参数变形展开方法与基函数方法结合的方法(DPTEM-BF)进行求解。最后通过图形分析了松弛时间参数、延迟时间参数、磁场参数等对速度场的影响。
2. 数学模型
考虑拉伸板上Oldroyd-B流体的非稳态驻点流动问题。建立如图1所示的流动示意图,其中,拉伸板的方向沿着x轴的方向,y轴垂直于拉伸板的方向。假设拉伸板的速度为 ,驻点流动速度为 ,其中 是常数。此外,沿着y轴方向施加了一个强度为B0的均匀磁场。

Figure 1. The physical flow diagram
图1. 流动示意图
Oldroyd-B流体的非稳态驻点流动控制方程为:
(1)
(2)
边界条件为:
当 时, , (3)
当 时, (4)
其中,u和v分别为沿x和y轴方向上的速度分量, 指的是流体的运动粘度系数,λ1和λ2分别是松弛时间参数和延迟时间参数。
采用如下的无量纲函数以及相似变量:
(5)
将(5)带入(2)~(4),得到对应的常微分方程及边界条件如下:
(6)
对应的边界条件转化为:
当 时, , (7)
当 时, (8)
其中, 和 分别为松弛时间参数和延迟时间参数, 为不稳定参数, 是驻点参数, 指的是磁场参数。
3. DPTEM-BF方法求解
采用双参数变形展开方法与基函数结合的方法求解微分方程,根据双参数变形展开方法的原理,对自变量和因变量进行变形,引入小参数ε和新变量ξ,将函数f(η)转化为:
, (9)
令 , ,其中a1,a2均为未知常数,F(ξ)为变量ξ的函数。
对应地,函数F(ξ)的初值条件为:
, , , (10)
将F(ξ)在 附近展开成级数形式:
(11)
将(10)带入(11)中,得到:
, , , , (12)
将(9)和(12)带入式(6)中,把微分方程转化为关于ε的多项式,根据多项式恒为零的性质,使多项式中ε同次幂的系数为零,再利用初值条件,便可以计算出Fi(ξ)的表达式,紧接着便可以得到F(ξ)的表达式,消去小参数ε,得到含有a1,a2的关于f(η)的表达式。采用结合基函数来确定参数a1,a2的值,将函数f(η)表示成如下基函数的组合:
(13)
其中,f0,0(η)为:
(14)
令 ,其中m1,m2,a0,a13,a23,a33为假设的未知数,最后使用牛顿迭代法便可以计算出每个未知参数的值,将其带入函数f(η)的表达式,就可以得到原微分方程的近似解析解。
4. 结果与讨论
采用双参数变形展开方法与基函数结合的方法求得了微分方程的近似解析解,由表1可知,将所求结果与已有的研究结果进行比较,具有很好的一致性。此外,通过图形详细分析讨论了各物性参数对速度场的影响。
Table 1. Comparison of − f ″ ( 0 ) with different values of S while β 1 = β 2 = A = M = 0
表1. 当 时,S取不同值, 值的比较结果
图2展示了松弛时间参数β1对速度场的影响,由图2可知,当β1增加时,流体的粘性力增大,这使得流体的流动阻力增大,因此流体的流动速度减小。
图3绘制了不同延迟参数值β2下的速度分布情况,从图中可以发现,延迟时间参数对速度场有着相反的影响,随着β2的增大,流体动量穿透深度加深,拉伸板上流体的速度分量增加,这意味着流体流速增加。此外,β2的增大也会使得流体动量边界层厚度变厚。
图4反映了不稳定参数S变化时速度场的变化趋势,由于S的增加,流体的流动速度以及边界层厚度都均匀地减小。
图5给出了驻点参数A对速度的影响,当A增加时,流体的动量损失减小,边界层内流体速度越快趋于周围流体速度,因此速度边界层厚度会变薄。
图6显示了磁场参数M变化时对速度的影响,随着M值的增大,流体的流动速度减慢,并且边界层厚度变薄。从物理上来讲,M的增加使得磁场作用下的洛伦兹力增大,这个力阻碍了流体流动,因此流体流动速度减小。

Figure 2. Influence of β1 on the velocity field
图2. β1对速度的影响

Figure 3. Influence of β2 on the velocity field
图3. β2对速度的影响

Figure 4. Influence of S on the velocity field
图4. S对速度的影响

Figure 5. Influence of A on the velocity field
图5. A对速度的影响
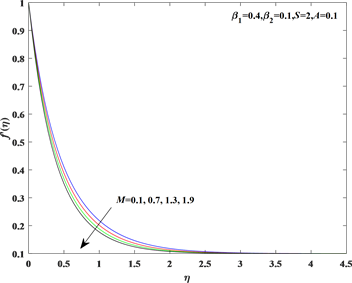
Figure 6. Influence of M on the velocity field
图6. M对速度的影响
5. 总结
本文研究了磁场对拉伸板上Oldroyd-B流体非稳态驻点流动的影响。通过合适的相似变换将控制方程转化为常微分方程,并且使用双参数变形展开方法与基函数方法结合的方法(DPTEM-BF)进行求解。采用图形详细分析了各物性参数对速度的影响,值得注意的是:随着驻点参数的增大,流体的动量损失减小,边界层内流体速度越快趋于周围速度,所以速度边界层厚度变薄;而磁场参数的增加会使得磁场作用下的洛伦兹力增大,这个力阻碍了流体流动,因此流体流动变缓。
基金项目
国家重点研究计划(2016YFC0700601),国家自然科学基金(21878018),北京市自然科学基金和北京市教育委员会联合资助项目(KZ201810016018),北京建筑大学市属高校基本科研业务费项目(X20142)。
文章引用
白羽,王清,张艳. 磁场作用下Oldroyd-B流体的非稳态驻点流动
Unsteady Stagnation-Point Flow of Oldroyd-B Fluid along a Stretching Sheet with Magnetic Field[J]. 现代物理, 2021, 11(01): 1-8. https://doi.org/10.12677/MP.2021.111001
参考文献
- 1. Khan, M., Mahmood, S. and Fetecau, C. (2009) New Exact Solutions for Magnetohydrodynamic Flows of an Oldroyd-B Fluid. Zeitschrift fur AngewandteMathematik und Physik, 60, 1206-1219. https://doi.org/10.1007/s00033-008-8029-7
- 2. Hayat, T., Ashraf, M.B., Al-Mezel, S. and Shehzad, S.A. (2015) Mixed Convection Flow of an Oldroyd-B Fluid with Power Law Heat Flux and Heat Source. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 37, 423-430. https://doi.org/10.1007/s40430-014-0165-8
- 3. Ullah, S., Khan, N.A., Bajwa, S., Khan, N.A., Tanveer, M. and Liaqat, K. (2017) Some Exact Solutions for the Rotational Flow of Oldroyd-B Fluid between Two Circular Cylinders. Advances in Mechanical Engineering, 9, 1. https://doi.org/10.1177/1687814017724702
- 4. Alshomrani, A.S., Salem, A., Irfan, M. and Khan, M. (2018) Chemically Reactive Flow and Heat Transfer of Magnetite Oldroyd-B Nanofluid Subject to Stratifications. Applied Nanoscience, 8, 1743-1754. https://doi.org/10.1007/s13204-018-0846-1
- 5. Hayat, T., Kiyani, M.Z., Ahmad, I. and Alsaedi, A. (2019) Double Stratified Radiative Flow of an Oldroyd-B Nanofluid with Nonlinear Convection. Applied Mathematics and Mechanics, 40, 1861-1878. https://doi.org/10.1007/s10483-019-2251-6
- 6. Hafeez, A., Khan, M. and Ahmed, J. (2020) Flow of Oldroyd-B Fluid over a Rotating Disk with Cattaneo-Christov Theory for Heat and Mass Fluxes. Computer Methods and Programs in Biomedicine, 191, Article ID: 105374. https://doi.org/10.1016/j.cmpb.2020.105374
- 7. Mustafa, M., Mushtaq, A., Hayat, T. and Alsaedi, A. (2015) Model to Study the Non-Linear Radiation Heat Transfer in the Stagnation-Point Flow of Power-Law Fluid. International Journal of Numerical Methods for Heat and Fluid Flow, 25, 1107-1119. https://doi.org/10.1108/HFF-05-2014-0147
- 8. Sharma, R., Ishak, A. and Pop, I. (2016) Stagnation Point Flow of a Micropolar Fluid over a Stretching/Shrinking Sheet with Second-Order Velocity Slip. Journal of Aerospace Engi-neering, 29, Article ID: 04016025. https://doi.org/10.1061/(ASCE)AS.1943-5525.0000616
- 9. Bai, Y., Liu, X.L., Zhang, Y. and Zhang, M. (2016) Stagnation-Point Heat and Mass Transfer of MHD Maxwell Nanofluids over a Stretching Surface in the Presence of Thermophoresis. Journal of Molecular Liquids, 224, 1172-1180. https://doi.org/10.1016/j.molliq.2016.10.082
- 10. Bai, Y., Xie, B., Zhang, Y., Cao, Y.J. and Shen, Y.P. (2019) Stagnation-Point Flow and Heat Transfer of Upper-Convected Oldroyd-B MHD Nanofluid with Cattaneo-Christov Double-Diffusion Model. International Journal of Numerical Methods for Heat and Fluid Flow, 29, 1039-1057. https://doi.org/10.1108/HFF-06-2018-0295
- 11. Hayat, T., Qasim, M., Shehzad, S.A. and Alsaedi, A. (2014) Un-steady Stagnation Point Flow of Second Grade Fluid with Variable Free Stream. Alexandria Engineering Journal, 53, 455-461. https://doi.org/10.1016/j.aej.2014.02.004
- 12. Zaib, A. and Shafie, S. (2015) Slip Effect on an Unsteady MHD Stagnation-Point Flow of a Micropolar Fluid towards a Shrinking Sheet with Thermophoresis Effect. International Journal for Computational Methods in Engineering Science and Mechanics, 16, 285-291. https://doi.org/10.1080/15502287.2015.1080317
- 13. Awais, A., Masood, K., Jawad, A., Abdul, H. and Zahoor, I. (2020) Unsteady Stagnation Point Flow of Maxwell Nanofluid over Stretching Disk with Joule Heating. Arabian Journal for Science and Engineering, 45, 5529-5540. https://doi.org/10.1007/s13369-020-04468-9
- 14. Mahdy, A. (2018) Modeling Unsteady Mixed Convection in Stagnation Point Flow of Oldroyd-B Nanofluid along a Convective Heated Stretched Sheet. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 40, 136. https://doi.org/10.1007/s40430-018-1052-5
- 15. Hayat, T., Qayyum, S., Waqas, M. and Alsaedi, A. (2018) Un-steady Stagnation Point Flow of Oldroyd-B Nanofluid with Heatgeneration/Absorption and Nonlinear Thermal Radiation. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 40, 84. https://doi.org/10.1007/s40430-018-1007-x
- 16. Asghar, S. and Ahmad, A. (2012) Unsteady Couette Flow of Viscous Fluid under a Non-Uniform Magnetic Field. Applied Mathematics Letters, 25, 1953-1958. https://doi.org/10.1016/j.aml.2012.03.008
- 17. Hayat, T., Shafiq, A., Alsaedi, A. and Asghar, S. (2015) Effect of Inclined Magnetic Field in Flow of Third Grade Fluid with Variable Thermal Conductivity. AIP Advances, 5, Article ID: 087108. https://doi.org/10.1063/1.4928321
- 18. Mabood, F., Abdel-Rahman, R.G. and Lorenzini, G. (2016) Numerical Study of Unsteady Jeffery Fluid Flow with Magnetic Field Effect and Variable Fluid Properties. Journal of Thermal Science and Engineering Applications, 8, Article ID: 041003. https://doi.org/10.1115/1.4033013
- 19. Jakati, S.V., Raju, B.T., Nargund, A.L. and Sathyanarayana, S.B. (2019) Study of Maxwell Nanofluid Flow over a Stretching Sheet with Non-Uniform Heat Source/Sink with External Magnetic Field. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 55, 218-232.
- 20. Hashmi, M.S., Khan, N., Mahmood, T. and Shehzad, S.A. (2017) Effect of Magnetic Field on Mixed Convection Flow of Oldroyd-B Nanofluid Induced by Two Infinite Isothermal Stretching Disks. International Journal of Thermal Sciences, 111, 463-474. https://doi.org/10.1016/j.ijthermalsci.2016.09.026
- 21. Sharidan, S., Mahmood, T. and Pop, I. (2006) Similarity Solutions for the Unsteady Boundary Layer Flow and Heat Transfer Due to a Stretching Sheet. International Journal of Applied Mechanics and Engineering, 11, 647-654.
- 22. Chamkha, A.J., Aly, A.M. and Mansour, M.A. (2010) Similarity Solution for Unsteady Heat and Mass Transfer from a Stretching Surface Embedded in a Porous Me-dium with Suction/Injection and Chemical Reaction Effects. Chemical Engineering Communications, 197, 846-858. https://doi.org/10.1080/00986440903359087
- 23. Mukhopadhyay, S., Ranjan De, P. and Layek, G.C. (2013) Heat Transfer Characteristics for the Maxwell Fluid Flow Past an Unsteady Stretching Permeable Surface Embedded in a Porous Medium with Thermal Radiation. Journal of Applied Mechanics and Technical Physics, 54, 385-396. https://doi.org/10.1134/S0021894413030061
