ABSTRACT

The formation and property of DNA loop are the basic problems of biophysics and soft matter physics. In present work, the conformational statistics is studied by Monte Carlo method based on the wormlike chain model. The priority conformational state for the different length of DNA loop is predicted and the force acting on the grafting point is also discussed.

Keywords: DNA Loop; Conformation; Monte Carlo Simulation

环形DNA分子构象统计

张兴华¹，肖弘毅²

¹北京交通大学理学院，北京

²北京师范大学物理系，北京

Email: zhangxh@bjtu.edu.cn, farxhy@mail.bnu.edu.cn

收稿日期：2014年1月3日；修回日期：2014年1月29日；录用日期：2014年2月10日

摘  要

DNA环的形成和性质是生物物理以及软物质物理关注的基本问题。本文以蠕虫状链为模型，应用蒙特卡洛方法模拟了锚定在蛋白质上的DNA环的构象统计。给出了DNA环在不同长度序列情况下的择优构象状态，讨论了不同构象情况下DNA分子对锚定点的作用力。

关键词

DNA环；构象；蒙特卡洛模拟

1. 引言

DNA环是由DNA分子的局部形成的环形构象。它的形成对于基因转录、重组和修复等的细胞生理过程中有着重要的影响^[1,2]。DNA分子通常要在小的尺度上表现出刚性的硬棒，而在较大尺度上表现出相对的柔性。描述这一特征的最简单模型是蠕虫状链(worm-like chain)模型^[3]。这个模型把高分子描述为不可伸长的弹性空间曲线。其弹性模量用键取向关联的持续长度(persistent length)来表征。它可以描述硬度从

完全刚性极限的线型分子到完全柔性极限的高斯链之间所有硬度的高分子链^[4]。

柔性高分子末端的分布函数只有一个极大值，即单峰分布，对应于熵主导的各向同性状态。在外场的作用下这个线团只是发生形变。对于完全刚性的线性分子，末端分布也有一个极大值，对应于一个构象状态：内能主导的各向异性状态。外场作用下，分子的响应主要是取向。而有限温度下蠕虫状链的末端分布函数呈现双峰分布对应于两个热力学稳定的状态，即分别是熵主导的各向同性构象和能量主导的各向异性状态共存。在外场作用下同时发生取向和形变。而当外场很大时两个状态间将发生相转变，这是一个一级相变^[5]。基于这一考虑处在环形状态下的DNA分子构象统计将更加丰富。Yamakawa把形式复杂的传播子变换到Fourier-Laplace空间；用图来表示各阶矩，通过定义新的求和规则来表示蠕虫状链模型的传播子，研究了半刚性高分子的J因子，即形成环的几率^[6]。研究发现，对于半刚性的DNA分子而言，在某一特定尺度上形成环是一个热力学的温度状态。近年来Spakowitz和王振纲进一步发展了Yamakawa的图方法^[7]，把Fourier-Laplace空间中用图方法对传播子的求解归结为相对简单的一维无规行走问题，并用形式简洁的连分数表达出来，用数值方法严格求解了这一问题。

现有的理论工作对于DNA环的热力学性质关注较多，然而对于在蛋白质辅助成环情况下，环的构象统计行为还了解不多，本工作关注锚定在蛋白质上的接枝DNA环的构象统计。用蒙特卡洛模拟方法预测在理想状况下DNA环的可能存在的构象^[8]。

2. 模型与方法

蠕虫状链模型把高分子模型化为空间中不可伸长的弹性曲线，其哈密顿量可以写为

其中β = 1/k_BT，l_p为为链取向关联长度，即持久长度L为整条分子链的长度，s为沿链方向的周线变量，u为取向。我们用蒙特卡罗方法计算环状DNA分子的构象统计。受限要把哈密度量离散化

其中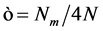，是表征链刚性的因子，N越大(即持久长度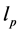越短，有效库恩长度a越短)，越小，链越柔软；反之，则越坚硬。此外还需要注意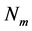，是离散变量，当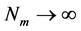时，上述约等号将变为等号；而当N→∞，半柔性链相应地退化为高斯链。

我们将初态选取为直观上能量最小的态，亦即，高分子链的每个节点都位于以x轴上原点和(d, 0, 0)为端点的一个优弧上，高分子链的两端与优弧的两端重合，且高分子链所在二维平面与xOy平面垂直，如图1所示。

假设我们将(a/2, 0, h)选取为优弧所在圆的圆心，那么优弧的角度为

如果高分子链中共有根键，则每根键对应的角度为

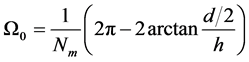
每根键的键长为

其中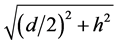为该优弧所在圆的半径。

在蒙特卡洛的抽样过程中我们采用局部的链运动的蒙特卡洛尝试移动。即随机选取一个分子(连接点)，随机取任意方向的单位矢量为轴，让该分子之后的分子链整体绕该轴旋转任意一个角度。在圈构象当中，这个方法具体化为：随机选取两个分子，以这两个分子的连线为轴，将这两个分子之间的链整体绕该轴旋转一个随机角度。矢量r绕单位矢量n旋转角度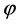，得到的新矢量r'可以表示如下：

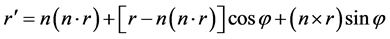
根据尝试移动前后的能量差，用Metropolis方法判断是否接受这一尝试移动。本文中的结果是在107个平衡构象的统计。而为了保证达到平衡，我们在统计前做了10⁵蒙特卡洛尝试移动。

图1. 初态的高分子链圈构象

当生成一个圈构象之后，我们有必要为它寻找一个序参量来表征它的形态。一个高分子链(质点系)的惯量张量为

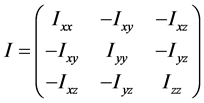
它是描述高分子绕一点转动时的惯性的物理量，其中、、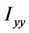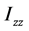称为x轴、y轴、z轴的转动惯量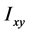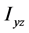，、、为惯量积，它们分别计算如下：

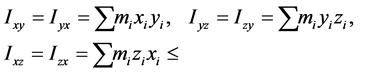
高分子链对定点转动的角动量表达式有

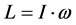
亦即

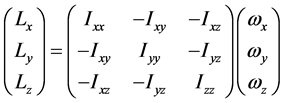
或者将矩阵形式改写成多项式形式

其中，i、j、k为坐标系各轴的单位矢量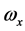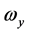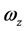，、、为角速度在该坐标系上的投影。

为了使惯量张量更加简明，我们需要寻找主轴坐标系。主轴坐标系中，所有惯量积为零，惯量张量可以对角化；由于惯量张量都是对称矩阵，其对角化是一定可以实现的。这时的惯量张量成为

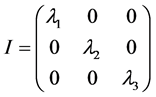
此时高分子对定点的角动量的表达式为

即

其中，i、j、k、、、的意义同上。根据上式，有

将上式作为主轴的另一定义，即，若高分子绕过定点某轴以角速度ω转动，而刚体对该点的角动量方向与角速度方向相同，则此轴就是该点的惯量主轴。上式变为

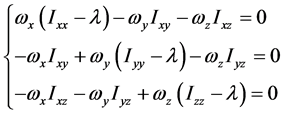
这组齐次线性方程组有非零解的条件为

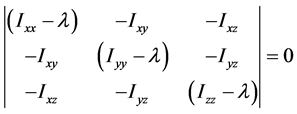
称为特征方程，它为λ的三次方程，根据由张量元组成的矩阵是实对称矩阵，此特征方程具有3个实根，它们是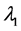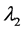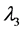，，，称为本征值，即刚体对三个主轴的转动惯量，也称主转动惯量；将本征值代回齐次线性方程组，求出与之对应的角速度矢量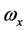、、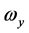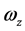为相应的本征矢量，其方向即三个主轴方向。

得到一个高分子链圈构象后，就可以根据如上方法，得出它的三个惯量主轴和三个主转动惯量，我们可以据此推测一些其形态方面的信息。

3. 结果与讨论

通过调节ε的取值，使得链分别具有显著的刚性或柔性。对于不同的构象我们通过模拟中的典型构象状态的快照来分析在分子链刚性较弱的情况下，DNA环分子表现为柔性。其统计特征为空间中的初始和末尾位置固定的随机行走。DNA分子处于构象熵占优的状态，这一行为与高斯链环的预言相同。这一结果相当于形成DNA环的分子较长的情况，图2给出了典型的长链DNA环(N = 10⁷)的构象快照。环的构象表现为各向同性的线团状形态。此时DNA分子环作用在锚定点上的力来自于接枝点对分子链随机行走的束缚，是一种熵力。

图2. 长链DNA分子环的构象

随着刚性的变强，我们得到的典型蠕虫状链圈构象如图3所示。随着刚性的增强，DNA分子链的行为偏离无规行走。而表现出较为伸展的构象。同时垂直于锚定平面的方向被挑选出来形成各向异性的结构。根据Spakowitz和王振纲的结论，半刚性高分子在中的硬度的情况下会自发形成环。对于我们关心的体系中给定了成环的分子链的硬度或长度后形成环的大小也就确定了，剩余的链段则倾向于平行排列以降低链的整体能量。这样就形成了具有发夹(hair-pin)结构的构象形态，这也是DNA分子中常见的环形态。此时DNA分子的锚定点上的应力也最小。容易形成稳定的DNA环结构。此外这一状态在高分子结晶问题中也有着极其重要的应用。通常高分子难以形成完全伸直链的晶体，而是形成折叠链的片晶。而片晶的折叠链表面则是由半刚性的环状高分子构成的高分子刷。因而我们在中等硬度的半刚性高分子环观察到的这种构象结构也将对高分子片晶热力学的理论研究大有裨益^[9]。

当刚性进一步增强，构象的涨落进一步降低。当刚性趋近于无穷大时，即刚性棒极限下，整个DNA分子处于能量择优的状态。对我们这里关注的接枝环，则形成一个撑开的环形。如图4所示。此时分子链中弹性能均匀分布在整条分子中。且接枝点上的受力也最大。因而对通过蛋白质锚定在一起的DNA环也不稳定。

针对三种不同柔性(ε值)的蠕虫状圈构象链，我们分别监测了它们在蒙特卡洛尝试移动操作中能量由初始构象变化至能量较稳定的平衡态的过程，并计算它们达到平衡态之后，进行不同次数的蒙特卡洛操作前后链能量的相关性，分别绘制了能量的变化曲线和相关系数的衰减曲线，如表1。

仔细对比不同柔性的蠕虫状链圈构象的能量变化图，不难得出，越柔软的链达到平衡需要经历的旋

图3. 中等长度DNA环的构象

图4. 锻炼DNA环的构象

转次数越多，而达到平衡之后其涨落也越大；而对比不同柔性的链的关联衰减图可知，柔性越显著的链，其相关系数在很少的旋转次数后就趋近于1，亦即它的关联长度越短。在以后的研究中，我们需要在链的能量趋于平衡之后的范围内、以大于关联长度的步长随机选取链作为样本进行进一步的考察和研究。

为了定量描述它的基本形态，我们根据上文中的公式求出它的惯量张量。通过计算我们发现，假设圈构象绕其质心转动，它的惯量主轴将近似为我们生成它时所建立的坐标系。我们将主轴坐标系下的主转动惯量两两作比得到的比值定义为偏心率，如下：

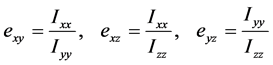
依次对初始的圈构象和N = 1，10，10⁷三种情形所生成的圈构象，在它们各自质心的主轴坐标系下求得偏心率并作系综平均，所得值分别如下表2所示。

偏心率的概念能够说明链的一些基本形态，例如，当偏心率反映出三个主转动惯量的比例大约为1:2:1时(初始圈构象和N = 1)，说明该链呈现为“碟形”(圆盘)，较大的主转动惯量所对应的惯量主轴即垂直于该“圆盘”的“中轴线”；如果偏心率反映出主转动惯量中有一个明显较小(N = 10和N = 10⁷)，则链的形态近似为“梭形”(圆柱)，而这一主转动惯量相应的惯量主轴就是“圆柱”的母线。(N从1增大到10的过

程中，圈构象从两边向中间收束，变为一个大体上垂直于xOy平面的修长的柱体，而当N继续向着10⁷变化时，圈构象向下坍塌。)因此，我们可以看到，随着链段的柔性逐渐增强，圈构象的形态由最开始非常紧张地向外扩张的圈状(由于界面下片晶层的作用，圈状将被修正为类似“蘑菇云”的形状)，从两边向着垂直界面的轴塌缩，变成“拱门”的形态，最后向着界面塌缩，变成一堆“线团”。

4. 结论

通过对锚定在蛋白质上的DNA分子环构象的蒙特卡洛模拟，我们发现对于柔性越显著的链 1) 达到平衡态所需的时间越久；2) 平衡态的平均能量越高；3) 达到平衡态之后所允许的能量涨落也越大；4) 达到平衡态之后，相同次数的操作前后平均能量的相关越小。另外，我们证明了惯量张量是可用于表征圈构象形态的良好的序参量，各个主转动惯量之间的比值(偏心率)表明了构象在相应维度上的扁平程度。目前进一步的研究仍在继续。

基金项目

中央高校基本科研业务费(2013JBM087)。

参考文献 (References)