Applied Physics
Vol.05 No.07(2015), Article ID:15712,9
pages
10.12677/APP.2015.57009
Study of the Interaction between Two Bubbles Based on OpenFOAM
Xia Zheng, Zhuangzhi Shen*, Xia Wang, Jia Yang, Li Li
College of Physics and Information Technology, Shaanxi Normal University, Xi’an Shaanxi
Email: *szz6@163.com
Received: Jun. 30th, 2015; accepted: Jul. 13th, 2015; published: Jul. 21st, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Applying the OpenFOAM software by adopting the SIMPLEC algorithm and VOF model of the PLIC, the motion characteristics of two bubbles (horizontal and vertical distribution) in still water were numerically simulated. The process of bubble shape deformation, the flow field changes around the bubbles, the interaction between the bubbles and flow field, and the influence of the separation distance and the width of container on bubbles motion were analyzed in detail. The results showed that the bubbles are symmetrically distributed in different shapes at different moments. Due to the existence of the vortex field, the two horizontal bubbles attract or repulse each other periodically in the process of rising, and meanwhile the bubbles will swing up. But, the two vertical distribution bubbles will coalesce or separate repeatedly. With the increasing distance of the two bubbles, the interaction strength becomes smaller. With the increasing width of the container, the influence of container on bubbles motion becomes smaller.
Keywords:SIMPLEC Algorithm, VOF Model, Bubble, Flow Field

基于OpenFOAM对两气泡间相互作用的研究
郑霞,沈壮志*,王霞,杨佳,李丽
陕西师范大学物理学与信息技术学院,陕西 西安
Email: *szz6@163.com
收稿日期:2015年6月30日;录用日期:2015年7月13日;发布日期:2015年7月21日

摘 要
本文基于OpenFOAM软件,选用SIMPLEC算法,采用VOF模型中的PLIC界面几何重构方法,模拟研究了二维水平分布和竖直分布的两气泡在静水中运动时形状的变化,周围流场变化及气泡与流场相互影响的整个过程,同时还分析了气泡间距,容器宽度对气泡运动的影响。结果表明:不同时刻,气泡在上升过程中以不同的形状对称分布,且由于涡流场的存在引起水平分布的两气泡在上升过程中反复的相互吸引和排斥,呈摇摆状上升;而垂直分布的两气泡则会出现反复融合和分离的现象。气泡间距越大,两气泡间的相互作用越小。容器越宽,气泡运动受其影响越小。
关键词 :SIMPLEC算法,VOF模型,气泡,流场

1. 引言
研究气泡在液体中的运动过程对自然现象和船舶工程、海洋工程、核能工程、生物工程、环境科学以及含气泡水体的水动力特性开展研究有着重要的理论和实际意义。一般气泡在液体中处于静止状态时不会对周围环境造成较大的影响,但气泡在液体中运动或破裂时能够引起压力波动,这会对设备和化学反应过程造成很大的影响[1] -[3] ,如船舶螺旋桨水流、水轮机和水泵的空化空蚀、废水处理,气液化学反应等,因此对气泡运动规律的研究也越来越受到国内外学者的关注,而对气泡运动界面的追踪是研究的重点。目前发展较成熟的界面追踪法有边界积分法[4] -[8] ,水平集法[9] [10] ,格子法[11] ,VOF法[12] [13] 等,在众多方法中VOF (Volume of Fluid)法以易实现、计算量小、模拟精度高等优点被广泛应用于模拟气泡运动方面。Robinson [14] 采用边界积分法分析了二维气泡在无粘流体中上升运动。焦焱[15] 采用了格子法对液体中的气泡聚并行为进行了模拟,分析了流体粒子间作用力下气泡聚并的影响因素。张淑君等[16] 采用VOF模型中的PLIC (Piecewise Linear Interface Calculation)界面追踪法,模拟了大量气泡在水中上升,变形,碰撞过程。本文选用OpenFOAM软件采用VOF模型中的界面几何重构法模拟了静水中水平放置和竖直放置的两气泡的运动过程,并分析探讨了气泡上升过程中的气泡的形变,周围流场的运动情况,以及流场对气泡运动的影响。
2. 数学模型
2.1. 模型简介
OpenFOAM (英文Open Source Field Operation and Manipulation的缩写),意为开源的场运算和处理软件)是对连续介质力学问题进行数值计算的C++自由软件工具包,其代码遵守GNU通用公共许可证。它可进行数据预处理、后处理和自定义求解器,常用于计算流体力学(CFD)领域。它对于处理一个算例由三个部分构成:前处理部分,求解部分,后处理部分。本文在数值模拟过程中使用的是OpenFOAM软件包中的多相流下的层流瞬态求解器interFoam,它是在有限体积法原理的基础上使用有界压缩的VOF法追踪气液两相界面的。
2.2. 控制方程
1) 不可压缩牛顿流体的连续性方程
 (1)
(1)
式中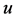 表示流体流动的速度,
表示流体流动的速度, 表示拉普拉斯算子。
表示拉普拉斯算子。
2) 考虑表面张力的动量方程
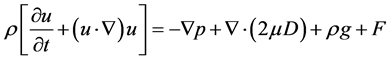 (2)
(2)
式中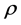 表示流体的密度,
表示流体的密度,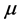 表示流体的粘滞度,
表示流体的粘滞度, 表示重力加速度,
表示重力加速度, 为应力张量,满足
为应力张量,满足
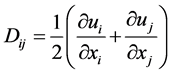
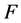 为表面张力,满足
为表面张力,满足

式中 表示表面张力系数,
表示表面张力系数,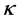 为交界面曲率,
为交界面曲率, 为气相体积分数,
为气相体积分数, 为气相密度,
为气相密度, 为液相密度。
为液相密度。
3) 采用VOF法追踪气泡界面的体积分数输运方程
 (3)
(3)
式中 为压缩界面的速度场,它只对界面区域产生影响,由于它的引入,OpenFOAM软件可以对交界面进行更为精确的追踪。
为压缩界面的速度场,它只对界面区域产生影响,由于它的引入,OpenFOAM软件可以对交界面进行更为精确的追踪。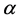 为计算区域网格中的流体体积分数,当
为计算区域网格中的流体体积分数,当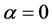 时,表示网格区域充满了目标流体;当
时,表示网格区域充满了目标流体;当 时,表示网格区域是空的;当
时,表示网格区域是空的;当 时,表示网格区域是多相流的交界面。
时,表示网格区域是多相流的交界面。
控制方程(1)中各体积单元的密度和动力粘度由体积分数决定


式中 ,
,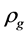 ,
, ,
, 分别为两种不同流体的密度和动力粘度。
分别为两种不同流体的密度和动力粘度。
本文选用的interFoam求解器采用PIMPLE算法求解不可压缩流体的连续性方程和动量方程,时间离散采用Euler格式,拉普拉斯项采用高斯积分的线性修正离散格式(Gauss linear corrected),压力梯度离散采用高斯积分的线性离散格式(Gauss linear)。体积分数方程中的对流项采用Gauss Vanleer格式,人工压缩项采用Gauss Interface Compression格式。
2.3. 参数设置
本文采用结构化网格,容器大小0.1 m × 0.2 m,相应的网格数为200 × 200个,容器的左右及底面均为无滑移边界,顶面为自由边界,表压为0 Pa,静水压为 Pa时间步长为0.0001 s,气泡初始半径为0.01 m,气泡中心距离容器底部0.01 m。气体和液体两相的物理参数分别采用20℃时的空气及水的物理参数,其中空气密度
Pa时间步长为0.0001 s,气泡初始半径为0.01 m,气泡中心距离容器底部0.01 m。气体和液体两相的物理参数分别采用20℃时的空气及水的物理参数,其中空气密度
 ,粘滞度
,粘滞度
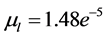 ,水密度
,水密度
 ,粘滞度
,粘滞度
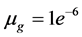 。表面张力系数
。表面张力系数
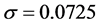 ,重力加速度
,重力加速度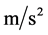
 气泡的初始速度为0,在浮力的作用下气泡在静止的流场中沿竖直方向上升。
气泡的初始速度为0,在浮力的作用下气泡在静止的流场中沿竖直方向上升。
3. 模拟结果与分析
当两个气泡在一起运动时,由于受到彼此的相互影响,所以运动过程要远比单泡在静水中的运动过程复杂的多,尤其是两个气泡相距比较近的时候,不仅其周围的流场结构会发生变化而且两气泡自身的形状和上升轨迹也会随之发生改变,同时气泡之间还可能发生碰撞和融合等现象。
3.1. 水平分布的两气泡在静水中运动的形变和流场变化
图1为水平放置中心间距为0.02 m的两气泡在时间t = 0 - 0.50 s内的形变和流场变化的二维图。图1(a)是t = 0 s时刻两气泡的初始状态图。由图1(b)可以观察到当t = 0.05 s时,在浮力作用下,两气泡同时向上运动,由于在上升过程中气泡上下表面之间存在压力差,底部压力大于顶部,所以底部开始凹陷,气


(a) (t = 0 s) (b) (t = 0.05 s)


(c) (t = 0.1 s) (d) (t = 0.15 s)

 (e) (t = 0.25 s) (f) (t = 0.30 s)
(e) (t = 0.25 s) (f) (t = 0.30 s)
 (g) (t = 0.40 s) (h) (t = 0.50 s)
(g) (t = 0.40 s) (h) (t = 0.50 s)
Figure 1. The deformation and the flow field changes of two bubbles of horizontal distribution in still water
图1. 水平分布的两气泡在静水中运动的形变及流场变化
泡发生形变。同时,在两气泡的左右侧会各产生形状近似为圆形的漩涡,两漩涡成对称分布,旋转方向相反,左侧气泡的漩涡按逆时针方向旋转,右侧气泡的漩涡则按顺时针方向旋转。另外,两气泡中间流体速度向上且大于气泡凹陷部分周围液体的运动速度,从而有指向两气泡中间的压力梯度,使两气泡向内倾斜,相互吸引,彼此靠近并呈两个对称的“瓢”状分布。当t = 0.10 s时如图1(c)所示,两气泡间流体速度叠加,使气泡底部的射流对气泡的作用点向叠加区域移动,而中间区域的两气泡壁面受到较大的射流推动,上升速度相应的加快。气泡两侧因受力不均衡发生旋转,两气泡向外倾斜,相互排斥,间距增大,气泡尾流部分形成的涡流场增强,两气泡呈“八”字形分布。随着两气泡间距的增大,两者相互影响变小,两气泡间区域内的流场水平分速度相互抵消作用变弱,此时两气泡的作用点会向气泡中心移动。当t = 0.15 s时如图1(d)所示,由于液体上表面的波动,带动整个流场,一段时间后气泡又彼此吸引,相互靠近,呈“鱼”状对称分布。当t = 0.25 s时如图1(e)所示,两气泡朝向左右边界面侧部分的速度大于气泡处于叠加区域的速度,两气泡相互靠近,并在强射流作用下,表面张力无法保持气泡原有的形状而使其破裂,由原来的两个变为四个气泡,大气泡呈倒“八”字形分布,小气泡则尾随其后。由于此时两气泡相距较近,中间区域的流场叠加会更加明显,从而气泡尾部的射流对气泡的作用点会再次向着叠加区域移动。如图1(f)、图1(g)、图1(h)分别是t = 0.30 s、t = 0.40 s、t = 0.50 s时的气泡运动图,靠近两气泡中间的叠加区域的气泡壁面受周围流场的推动作用,其速度逐渐变大,加之液体上表面的摆动作用,气泡周围的流场在增强的同时变得更加复杂,由原来的两个旋涡先变为四个,最后变为六个。水平分布的两气泡在整个上升过程中总是以不同形状对称分布,另外,由于射流的流动分隔作用使两气泡总是在先相互吸引后相互排斥的交替状况下呈摇摆状不断向上运动,直到与自由界面融合。
3.2. 竖直分布的两气泡在静水中运动的形变和流场变化
图2给出了竖直放置中心间距为0.02 m的两气泡在时间t = 0 - 0.45 s内的形变和流场变化的二维图。图2(a)是t = 0 s时刻两气泡的初始状态图。开始阶段,两气泡在浮力作用下缓慢上升,当t = 0.03 s时,气泡在其表面压力差的作用下,两侧界面处产生漩涡,从而开始发生形变,如图2(b)所示,上部气泡呈“球帽状”,下部气泡呈“梨”状。随着气泡的加速上升,当t = 0.04 s时如图2(c)所示,在压力梯度和气泡表面发展形成的涡流的共同作用下产生较强射流,使上部气泡的底部受到较大的冲击作用后呈“月牙”状,而下部气泡在上部气泡的尾流的抽吸作用下逐渐的向上部气泡的底部靠近,并呈“裙边”状。气泡在相互碰撞之前,为了能够有一个比较光滑的接触面,中间都会有一层薄液膜使两泡处于相互分离
的状态,而当两气泡相互接触且薄液膜被拉长时两气泡逐渐融合。当t = 0.05 s时,在粒子间作用力和涡流的作用下,下部气泡的上升速度大于下部气泡的上升速度,随着两气泡的不断靠近逐渐融合为一个气泡,如图2(d)所示。由于融合后的气泡变大,所以气泡表面及周围的流场变得更强,尤其是气泡的正下方会产生更强的射流,使气泡在射流的剧烈冲击下发生更大的形变,呈一环形的“桃”状结构,如图2(e)所示。当t = 0.20 s时,气泡在射流的强烈冲击作用下表面张力因无法维持其原有形状而发生破裂,由融合后的一个大气泡破裂成三个小气泡,其中有两个呈“靴”状对称分布在较大气泡的下方,如图2(f)所


(a) (t = 0 s) (b) (t = 0.03 s)


(c) (t = 0.04 s) (d) (t = 0.05 s)

 (e) (t = 0.15 s) (f) (t = 0.20 s)
(e) (t = 0.15 s) (f) (t = 0.20 s)
 (g) (t = 0.30 s) (h) (t = 0.45 s)
(g) (t = 0.30 s) (h) (t = 0.45 s)
Figure 2. The deformation and the flow field changes of two bubbles of vertical distribution in still water
图2. 竖直分布的两气泡在静水中运动的形变和流场变化
示。随着气泡的不断上升,两个小气泡会被涡流向上卷起,由于它们的运动速度大于较大气泡的速度,因此三者再次产生了融合现象,如图2(g)、图2(h)所示。图2(h)中气泡被横向拉伸,变为一个极不规则的大气泡,并缓慢的向上移动直到与自由界面相融合。
3.3. 气泡间距对气泡形变和流场的影响
图3为半径R = 0.01 m,中心间距分别为3R,4R的两气泡以不同的分布方式在t = 0.05 s时的形变和流场变化图。由图1(b)和图3(a),图3(b)可知,水平放置的两气泡在同一时刻,不同间距下气泡的形变和流场结构均不同,且随着间距的不断增大,两者间的相互作用效果逐渐变弱,两气泡间流体的流场强度减弱,气泡形变及流场结构越来越接近单个气泡在静水中自由上升的特性。由图2(d)与图3(c),图3(d)可知,竖直放置的两气泡在同一时刻,不同间距下气泡的形变和流场结构也不同,且随着间距的不断增大,两气泡间流体的流场强度不断减弱,导致上部气泡对下部气泡的抽吸作用减小,上部气泡上升速度增大下部气泡上升速度减小,使两气泡发生融合现象的时间变长。
3.4. 容器宽度对气泡形变和流场的影响
图4为水平放置,间距s = 2R的两气泡,在t = 0.25 s时,分别在宽度L为6R,14R的容器中的形变和流场图。由图4(a)和图4(b)可以观察到,在气泡大小和间距一定的情况下,容器越宽,气泡的运动对周围流体的扰动越小,尤其对容器壁处的流体扰动更小。相反,容器壁对气泡的运动状态的影响越小,流场结构越简单。
图5为t = 0.25 s时,水平放置的两气泡在接近容器壁处不同高度上流场水平分速度的曲线图。在图5中,两气泡的半径R = 0.01 m,间距s = 2R。由图5可以观察到,当容器的宽度L = 6R时,气泡的运动对周围流体的扰动作用最大,在0~0.06 m的高度范围内容器壁附近的流场水平分速度出现多个不同的峰值,流场的变化最复杂,气泡间的相互作用和形变受容器壁的影响也最大。当L = 8R时,气泡对流体的扰动作用逐渐减弱,在距离容器底部0.02 m处,流场的水平分速度出现最大值。当L = 10R时,气泡对流体的扰动作用明显减弱,流场的速度会出现较小的峰值,容器宽度对气泡运动的影响越来越小。当L = 12R,14R时,气泡的运动受容器壁的影响非常小,两气泡近似在无限大的流场中自由运动。由此可知,在t = 0.25 s时气泡间距一定的情况下,处在0~0.06 m高度范围内,气泡运动对流体的扰动会随容器

 (a) (s = 3R) (b) (s = 4R)
(a) (s = 3R) (b) (s = 4R)
 (c) (s = 3R) (d) (s = 4R)
(c) (s = 3R) (d) (s = 4R)
Figure 3. The influence of distance on bubble deformation and flow field
图3. 间距对气泡形变和流场的影响

 (a) (L = 6R) (b) (L = 14R)
(a) (L = 6R) (b) (L = 14R)
Figure 4. The influence of container width on flow field
图4. 容器宽度对流场的影响
宽度的增大而减小,在高度超出0.06 m以后容器宽度不会对气泡运动产生较大的影响。

Figure 5. The horizontal velocity of flow field
图5. 流场的水平分速度
4. 结论
本文基于OpenFOAM软件,采用VOF模型中的界面几何重构法,对静水中气泡的自由上升过程进行了二维的数值模拟,模拟结果符合一般的物理规律,并得到如下结论:1) OpenFOAM软件能较精确的模拟气泡在水中的运动过程。2) 气泡在水中自由上升的过程中,表面张力对气泡的形变过程起重要的作用。3) 压力差是气泡产生射流的主要原因。4) 容器越宽,气泡受容器壁的影响越小,气泡运动对流体的扰动作用越小。5) 在静水中水平分布的两气泡在上升过程中不同时刻总是以不同的形状对称分布,并且在涡流场的影响下,两气泡会先相互吸引后相互排斥呈摇摆状不断上升,不会发生碰撞和融合现象。同时,随着气泡间距的增大,二者间的相互作用效果会减弱,气泡的运动特性会逐渐接近单气泡的运动形式。6) 对于竖直放置的两气泡,由于上部气泡的尾流对下部气泡有抽吸作用所以使下部气泡在上升过程中的速度大于上部气泡,从而发生气泡的融合现象,但是随着气泡射流的加剧,气泡会再次分离然后再融合直到气泡与自由界面结合为止。随着气泡间距的增大,气泡间的速度差会增大导致气泡间发生融合现象的时间会变长,甚至不会出现融合现象。
基金项目
国家自然科学基金项目(NO11174191)。
文章引用
郑 霞,沈壮志,王 霞,杨 佳,李 丽, (2015) 基于OpenFOAM对两气泡间相互作用的研究
Study of the Interaction between Two Bubbles Based on OpenFOAM. 应用物理,07,61-70. doi: 10.12677/APP.2015.57009
参考文献 (References)
- 1. 康灿, 周亮, 王育力 (2013) 磨料水射流冲击材料壁面的模拟与实验. 江苏大学学报, 3, 276-280.
- 2. Dahikar, S.K., Gulawani, S.S. and Joshi, J.B. (2007) Effect of nozzle diameter and its orientation on the flow pattern and plume dimensions in gas-liquid jet reactors. Chemical Engineering Science, 62, 7471-7483. http://dx.doi.org/10.1016/j.ces.2007.08.035
- 3. Zhou Q.L., Li, N. and Chen, X. (2009) Analysis of water drop erosion on turbine blades based on a nonlinear liquid solid impact model. International of Impact Engineering, 36, 1156-1171. http://dx.doi.org/10.1016/j.ijimpeng.2009.02.007
- 4. Lorstad, D. and Francois, M. (2004) Assessment of volume of fluid and immersed boundary methods for droplet calculations. International Journal for Number Methods in Fluids, 46, 106-125. http://dx.doi.org/10.1002/fld.746
- 5. Tryggvason, G., Bunner, B. and Esmaeeli, A. (2001) A front tracking method for the computations of multiphase flow. Journal of Computational Physics, 169, 708-759. http://dx.doi.org/10.1006/jcph.2001.6726
- 6. 宗智, 何亮, 张恩国 (2007) 水中结构物附近三维爆炸气泡的数值模拟. 水动力学研究与进展, 5, 592-602.
- 7. 张阿漫, 姚熊亮 (2008) 近自由面水下爆炸气泡的运动规律研究. 物理学报, 1, 339-352.
- 8. 张阿漫, 姚熊亮 (2008) 单个三维气泡的动力学特性研究. 应用力学学报, 1, 107-111.
- 9. Osher, S. and Fedkiw, R.P. (2001) Level set methods, an overview and some recent results. Journal of Computional Physics, 169, 463-502. http://dx.doi.org/10.1006/jcph.2000.6636
- 10. Sussman, M., Smereka, P. and Osher, S. (1994) A level set approach for computing solutions to incompressible two-phase flow. Journal of Com-putional Physics, 114, 146-159. http://dx.doi.org/10.1006/jcph.1994.1155
- 11. Watanable, T. and Ebihara, K. (2003) Numerical simulation of coalescence and breakup of rising droplets. Computational Fluids, 32, 832-834.
- 12. Puckett, E.G., Almgren, A.S. and Bell, J.B. (1997) A high-order projection method for tracking fluid interfaces in variable density incompressible flows. Journal of Computional Physics, 130, 269-282. http://dx.doi.org/10.1006/jcph.1996.5590
- 13. 端木玉, 朱仁庆 (2007) 流体体积方程的求解方法. 江苏科技大学学报: 自然科学版, 2, 10-15.
- 14. Robinson, P.B., Boulton-Stone, J.M. and Blake, J.R. (1995) Application of boundary integral method to the interaction of rising two-dimensional, deformable gas bubbles. Journal of Engineering Mathematics, 29, 393-412. http://dx.doi.org/10.1007/BF00043975
- 15. 焦焱 (2009) 气泡运动的格子Boltzmann方法模拟. 硕士论文, 哈尔滨工业大学, 哈尔滨.
- 16. 张淑君, 吴锤结 (2008) 气泡之间相互作用的数值模拟. 水动力学研究与进展, 6, 683-684.