Applied Physics
Vol.
11
No.
05
(
2021
), Article ID:
42108
,
6
pages
10.12677/APP.2021.115028
基于激光光源测凸透镜焦距方法对比研究
苏学军,柳叶*,刘存海
海军航空大学航空基础学院,山东 烟台
收稿日期:2021年3月22日;录用日期:2021年4月23日;发布日期:2021年4月30日

摘要
本文对测量凸透镜焦距的传统实验方法进行改进,采用激光作为光源进行测量的一种新型方法。此方法基于凸透镜汇聚光线,激光沿直线传播,平面镜成像等原理,可直接读取焦距测量值,综合性较强,结果较传统方法更准确。
关键词
焦距,激光,凸透镜,平面镜
Comparative Study on Measurement of Focal Length of Convex Lens Based on Laser Source
Xuejun Su, Ye Liu*, Cunhai Liu
Aeronautical Basic College, Naval Aviation University, Yantai Shandong

Received: Mar. 22nd, 2021; accepted: Apr. 23rd, 2021; published: Apr. 30th, 2021

ABSTRACT
In this paper, the traditional experimental method of measuring focal length of convex lens is improved, and a new method of measuring the focal length of convex lens using laser as light source is introduced. This method is based on the principle of convex lens converging light, laser propagating along a straight line, plane mirror imaging and so on. It can directly read the measurement value of focal length, which is more comprehensive and more accurate than that of traditional method.
Keywords:Focal Length, Laser, Convex Lens, Plane Mirror

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
测量凸透镜的方法有很多——自准直法、平行光管法、位移法等 [1] [2] [3] [4],实验中通常采用可以获取实像的方法来达到测量和计算的目的,对于凸透镜而言,实物分别在一倍焦距以上和二倍焦距以上,均可获得实像,就可以利用公式法或位移法进行测量。本文在公式法和位移法的研究的基础上,又对自准直法加以改进,实验选用激光作为光源,由于激光具有很好的单色性和很强的方向性,可以使实验中光源的会聚效果更明显,实验中仅采用了凸透镜和平面反射镜即可快速准确地测量凸透镜的焦距。实验原理就是利用了平行光经凸透镜会聚至焦点、平面反射镜成像等原理 [5] [6] [7],实验中利用激光的直线传播,作为平行光源,凸透镜焦距可以直接读取,与位移法和公式法相比,虽然平行光的调节要求更高一些,但测量结果精度更好。
2. 透镜焦距测量原理
2.1. 基于激光光源的自准直法
如图1所示,将激光光源调整好,使出射光源与光具座平行即与薄凸透镜主光轴平行,在实验中利用一个带小孔的白屏调节准直。在平面镜上标注基准O点,在像屏上标注O'点、A点和A'点,A与A'关于O'点对称,平面反射镜沿着光具座由远及近缓慢移动,当出射光线经薄凸透镜透射,再由平面镜反射,再次经薄凸透镜透射后,透射点与像屏上标注点A'一致时,平面镜停止移动,此时平面反射镜与薄凸透镜之间的距离就是待测透镜的焦距。
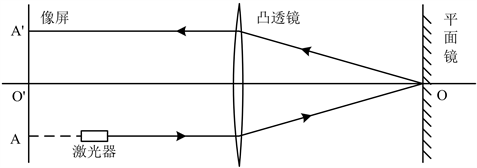
Figure 1. Experimental schematic diagram of lens focal length measurement based on laser light source
图1. 基于激光光源测透镜焦距实验原理图
2.2. 公式法
如图2所示,在光具座上分别放置物、凸透镜和像屏,并采用位移法进行光路细调,使各光学元件等高共轴,将物与透镜间的距离保持一倍焦距以上,在物关于透镜对称方移动像屏获可得一清晰的像(也可使物与像屏之间保持一定距离,移动透镜)。此时分别记录物、透镜和像屏的位置,即可计算出物距p、像距p'分别为自透镜中心处至物、像间的距离。当物、像为实物和实像时,对应的符号为正;反之为负。
在近轴条件下,根据薄透镜物像公式 可以测得透镜焦距。

Figure 2. Measurement of focal length of convex lens by formula method
图2. 公式法测透镜焦距
2.3. 位移法
根据凸透镜成像规律,当物距大于一倍焦距的时候,所成的像均为倒立的实像,并且随着物距的增大,所成实像由放大、等大(物距等于两倍焦距)、缩小逐渐变化。如图3所示,如果保持物屏和像屏之间的距离L >
和缩小的实像。CD间距离为l,通过公式 ,实验时,只要分别记录ABCD的位置,根据公式
即可计算焦距。
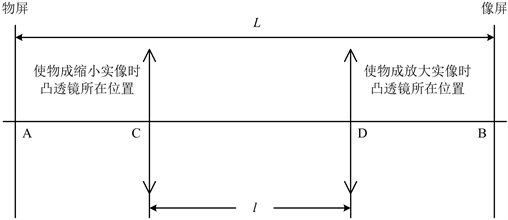
Figure 3. Measurement of focal length of convex lens by displacement method
图3. 位移法测薄凸透镜焦距
3. 实验结果比较
3.1. 基于激光光源的自准直法
根据表1中测量数据可计算透镜焦距测量列的最佳值是: 。
由贝塞尔公式可知测量列的标准差为: 。
测量列的A类标准不确定度 。
置信概率为0.683时, A类不确定度: (10次测量可查表 )。
实验中测量工具为米尺,服从正态分布,置信系数C = 3,分度之为1 mm,仪器误差 ,B类标准不确定度为 。
B类不确定度为 ( )。
透镜焦距测量值的合成标准不确定度为 。
测量结果为: (置信概率为0.683)。
相对误差为: 。
Table 1. Lens focal length data based on laser light source
表1. 基于激光光源测透镜焦距数据记录(cm)
3.2. 公式法
根据表2中测量数据可计算透镜焦距平均值: ;置信概率为0.683时,A类不确定度: ;B类不确定度: ;测量值的合成标准不确定度: ;测量结果为: ;相对误差: 。
Table 2. Formula method data record table
表2. 公式法数据记录表格(cm)
3.3. 位移法
根据表3中测量数据可计算透镜焦距平均值: ;可计算出置信概率为0.683时,A类不确定度: ;B类不确定度: ;测量值的合成标准不确定度: ;测量结果为: ; 相对误差: 。
Table 3. Displacement method data recording table
表3. 位移法数据记录表格
4. 三种方法对比
基于激光光源的自准直法避免了传统自准直法干扰像的困扰,同时反射后的光点采用激光光源后位置便于确定,可以直接读取透镜的焦距。
公式法测量薄凸透镜焦距需要提前对透镜的焦距进行粗略估计,当然这一点是比较容易实现的,引起误差的原因主要有两个,一方面是像的清晰度的判断,是否清晰,哪里清晰,具有一定的主观性,如果实验中是移动像屏来获得清晰的像,测量结果影响像距的大小,如果实验中是移动透镜获得清晰的像,测量结果会影响到物距和像距的大小,从而直接影响到测量结果;另一方面是透镜光心的位置很难确定并且各个元件中心位置不确定,会造成物距和像距都存在一定的偏差,由于在实验中各元件位置的不确定会引起一定的误差。
位移法在测量过程中,每次测量相当于进行了两次公式法测量,同等情况下相当于公式法两次测量取了平均值,避免了公式法的光心位置的确定,可以准确的确定L与l,因此比公式法要更准确一些,但在调节的过程中凸透镜位置的确定很难唯一,对于像的清晰度的判断依人而定,无法明确,两次确定的C、D位置都存在一定的人为因素(图3所示),尤其是在所呈现的放大的实像时,所成实像会在一定的范围内都比较清晰,虽然采用了左右逼近法读取数据,但主观的猜测性很强,不同的人员测定数据是有一定的差距,因此结果会有一定偏差。
Table 4. Error comparison of three methods
表4. 三种方法误差比较(cm)
从表4的误差比较可以看出,利用激光自准直法测量薄凸透镜焦距较其他两种方法更好一些,A类不确定度明显是基于激光光源的自准直法更好一些,由于三种方法的B类不确定度一样,因此合成不确定度相差没有那么明显。从三种方法误差分析数据可以看出位移法较公式法要稍微好一些,这是由于位移法不需要确定透镜光心的位置,只需要各元件之间的距离差就可以了,因此避免了不必要的误差,由于位移法在测量焦距的时候要提前估计一下透镜的焦距,而且物与像屏之间距离的不同引起误差大小也不同 [8],因此这种方法还是具有一定的局限性。
5. 结论
本文分别采用基于激光光源的自准直法、公式法和位移法测量了薄凸透镜的焦距,从实验结果来看,明显是采用激光光源的自准直法要优于另外两种方法,本实验采用的自准直法,是通过光源改善,提高了实验的精度,选用了准直性好的激光作为光源。位移法与公式法的误差来源,主要是成像清晰度的判定,存在较大的人为因素,视觉的判断能力。而传统的自准直法也存在这方面的误差,通过光源的改变,可以通过观察激光达到准确定位,提高实验精度;该方法原理简单,操作方便,就是利用了平行光经凸透镜后会聚与焦点,而平行光的获得是采用了激光。本方法有着很明显的先进性、创造性和实用性。
文章引用
苏学军,柳 叶,刘存海. 基于激光光源测凸透镜焦距方法对比研究
Comparative Study on Measurement of Focal Length of Convex Lens Based on Laser Source[J]. 应用物理, 2021, 11(05): 247-252. https://doi.org/10.12677/APP.2021.115028
参考文献
- 1. 陈舟, 倪敏. 平凸透镜焦距的测量与研究[J]. 物理通报, 2018, 37(4): 71-78.
- 2. Yang, G., Miao, L., et al. (2018) High-Accuracy Measurement of the Focal Length and Distortion of Optical Systems Based on Interferometry. Applied Optics, 57, 5217-5223. https://doi.org/10.1364/AO.57.005217
- 3. Huang, Y., Wang, C., et al. (2017) High-Precision Measurement of Focal Length for Long-Focus Infrared Optical System. Journal of Applied Optics, 38, 995-998. https://doi.org/10.5768/JAO201738.0606002
- 4. 李林, 黄一帆. 应用光学[M]. 北京: 北京理工大学出版社, 2017.
- 5. 李晓磊. 基于平行光管法的薄凸透镜焦距测量[J]. 应用光学, 2019, 40(5): 859-862.
- 6. 饶世贤, 刘仁明. 用激光测量凸透镜的焦距[J]. 物理通报, 2011(5): 57-58.
- 7. 方光宇, 辛丽, 赵海发, 等. “薄透镜焦距测定”实验的教学探讨[J]. 物理实验, 2017, 37(9): 30-34.
- 8. 柳叶, 刘存海, 等. 位移法测量透镜焦距的最佳位置分析[J]. 应用物理, 2019, 9(4): 157-162.
https://doi.org/10.12677/APP.2019.94019
NOTES
*通讯作者。
