Computer Science and Application
Vol.2 No.2(2012), Article ID:731,5 pages DOI:10.4236/CSA.2012.22010
A Critical Path Spanning Tree Algorithm Based on Breadth-First Traversal*
School of Automation, University of Science and Technology, Beijing
Email: liandingfu@126.com
Received: Apr. 21st, 2012; revised: May 14th, 2012; accepted: May 25th, 2012
ABSTRACT:
To get critical path is of great significance for the use of critical path method in project management. This paper first defines project management graph model, and then puts forward a critical path spanning tree algorithm based on breadth-first traversal, and then achieves the optimization algorithm through the research of the model. The simulation shows that the algorithm can create a tree which keeps the maximum path from the root node to any node in the graph model, and get the critical path easily through the tree.
Keywords: Project Management Graph Model; Spanning Tree; Critical Path; Breadth-First Traversal
基于广度优先遍历的关键路线生成树算法*
付冬梅1,练丁榑2
北京科技大学自动化学院,北京
Email: liandingfu@126.com
摘 要:
关键路线的确定对于运用关键路线法进行项目管理具有十分重要的意义。本文首先定义了项目管理图模型,然后在此基础上提出了一种基于广度优先遍历的关键路线生成树算法,最后通过对项目管理图模型的研究,实现了对算法的优化。仿真结果表明,该算法能够生成一棵保留根节点到任意节点最大路径信息的树,通过生成的树能够方便地确定关键路线。
收稿日期:2012年4月21日;修回日期:2012年5月14日;录用日期:2012年5月25日
关键词:项目管理图模型;生成树;关键路线;广度优先遍历
1. 引言
网络计划技术是指用于工程项目的计划与控制的一项管理技术,自二十世纪五十年代兴起以来,网络计划技术已经被许多国家认为是当今最行之有效的、先进的、科学的管理方法[1]。关键路线法(CPM)作为网络计划技术的一个核心工具,实施多年以来在各个领域都得到了普遍的运用,并取得了巨大的成功[2]。该方法用网络图表示各项工作之间的相互关系,通过找出控制项目工期的关键路线,在一定工期、成本、资源条件下获得最佳的计划安排,以达到缩短工期、提高工效、降低成本的目的。
建立项目的网络图模型之后,关键路线的寻找能够采用动态规划方法进行求解[3]。但是,现代工程项目正朝着大型化、规模化的方向发展,与之对应的网络图复杂度也呈指数级增长,动态规划方法面临着网络图存储管理难度大、关键路线计算复杂等挑战[4]。同时,动态规划这类传统方法仅仅对网络图的关键路线进行计算,缺乏对整个网络图模型的研究,从而忽视网络图中许多重要的信息。随着计算机技术的不断发展,利用计算机相关理论,通过设计相应算法,可以较好的解决上述问题。
关键路线法建立的项目网络图模型可以看作一类特殊的图模型,因此可以用图论的相关理论进行计算和处理。本文根据利用关键路线法建立的项目网络图的特点,提出了项目管理网络图模型,并针对该模型提出了一种算法,能够遍历项目管理图模型,并计算出图中任何每个节点到根节点的关键路线[5],最终生成一棵保留了根节点到任意节点最大路线信息的树。
2. 图的相关理论
2.1. 有向图的概念和表示
图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。定义为:二元组( ,
,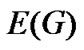 )称为图(graph)。其中(
)称为图(graph)。其中( )是一个非空的结点(或叫顶点)集合,其成员称为结点或顶点。
)是一个非空的结点(或叫顶点)集合,其成员称为结点或顶点。 是边(或叫弧)的集合,其成员称为边或弧。
是边(或叫弧)的集合,其成员称为边或弧。
如果给图的每条边规定一个方向,那么得到的图称为有向图,其边也称为有向边。在有向图中,与一个节点相关联的边有出边和入边之分,而与一个有向边关联的两个点也有始点和终点之分。一个有向图 由非空有限集
由非空有限集 和
和 构成。
构成。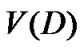 叫做有向图
叫做有向图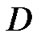 的顶点集,
的顶点集, 叫做有向图
叫做有向图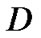 的弧集,顶点集
的弧集,顶点集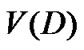 的每一个元素称作有向图
的每一个元素称作有向图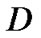 的顶点,
的顶点,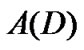 中的每一个元素称作有向图
中的每一个元素称作有向图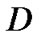 的弧[6]。
的弧[6]。
要表示一个有向图 ,有两种标准方法,即邻接表和邻接矩阵,由于本文主要用邻接表表示有向图,因此主要介绍有向图的邻接表表示法。邻接表表示法根据邻接表中存储的内容的不同又可分为子邻接表和父邻接表两种表示形式,这两种形式在数学上是完全等价的,可以直接从一种表示法推出另一种表示法。本文后面提到的回溯最大路线算法采用的是父邻接表表示方法,广度优先遍历采用子邻接表表示方法。
,有两种标准方法,即邻接表和邻接矩阵,由于本文主要用邻接表表示有向图,因此主要介绍有向图的邻接表表示法。邻接表表示法根据邻接表中存储的内容的不同又可分为子邻接表和父邻接表两种表示形式,这两种形式在数学上是完全等价的,可以直接从一种表示法推出另一种表示法。本文后面提到的回溯最大路线算法采用的是父邻接表表示方法,广度优先遍历采用子邻接表表示方法。
有向图 的子邻接表表示由一个包含
的子邻接表表示由一个包含![]() 个列表的数组
个列表的数组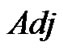 组成。对于每一个顶点
组成。对于每一个顶点 ,邻接表
,邻接表 包含所有满足条件的
包含所有满足条件的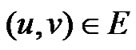 的顶点
的顶点![]() [7]。如图1中(a)所示的有向图,用邻接表表示为如图1中(b)所示。
[7]。如图1中(a)所示的有向图,用邻接表表示为如图1中(b)所示。
有向图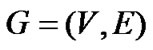 的父邻接表表示也由一个包含
的父邻接表表示也由一个包含![]() 个列表的数组
个列表的数组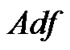 组成。对于每一个顶点
组成。对于每一个顶点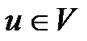 ,邻接表
,邻接表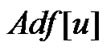 包含所有满足条件的
包含所有满足条件的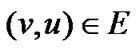 的顶点v。对于如图1中(a)所示的有向图,用邻接表表示为如图1中(c)所示。
的顶点v。对于如图1中(a)所示的有向图,用邻接表表示为如图1中(c)所示。
2.2. 图的广度优先遍历
图的广度优先搜索遍历算法是一个分层遍历的过程,和二叉树的广度优先搜索遍历类同。基本思想是:从 出发,访问
出发,访问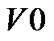 的各个未曾访问的邻接点
的各个未曾访问的邻接点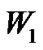 ,
,![]() ,…,
,…,![]() ;然后,依次从
;然后,依次从 ,
,![]() ,…,
,…,![]() ;出发访问各自未被访问的邻接点,直到全部顶点都被访问为止[8]。
;出发访问各自未被访问的邻接点,直到全部顶点都被访问为止[8]。
对于图2所示的连通图,若顶点![]() 为初始访问的顶点,则广度优先搜索遍历顶点访问顺序是:
为初始访问的顶点,则广度优先搜索遍历顶点访问顺序是:![]() →
→ 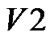 →
→ 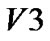 →
→ 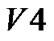 →
→ 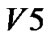 →
→ 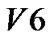 →
→  →
→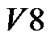 。遍历过程如图2所示。
。遍历过程如图2所示。
 (a)
(a)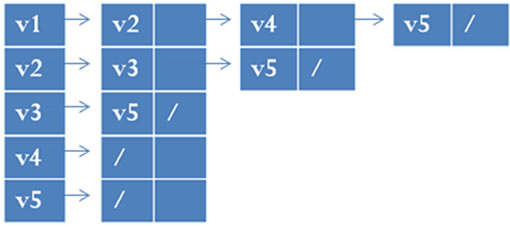 (b)
(b)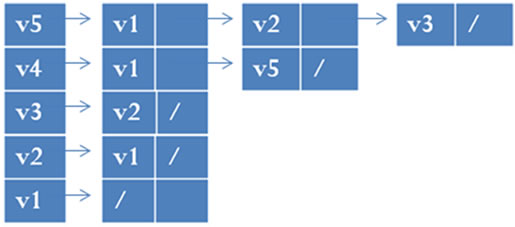 (c)
(c)
Figure 1. Two representation of digraph. (a) Digraph G; (b) Son adjacency list of G; (c) Father adjacency list of G
图1. 有向图的两种表示法。(a) 有向图G;(b) G的子邻接表表示;(c) G的父邻接表表示
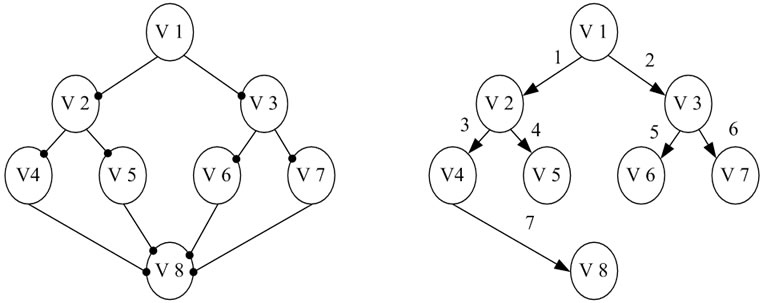
Figure 2. Breadth-first traversal of graph
图2. 图的广度优先搜索遍历
2.3. 项目管理图模型的定义
本文根据一般项目管理的任务划分提出了一种项目管理有向图模型,具体定义如下:
对于有向图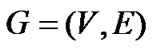 [9],如果它满足以下条件:
[9],如果它满足以下条件:
(1) 存在一个所有节点的根节点,不具有实际意义,仅表示项目的开始,该节点没有父节点;
(2) 根节点外的每个节点表示项目的一道工序或一个任务,节点属性可以包括项目某道工序或任务的编号、名称、工期等信息;
(3) 节点之间的箭线表示工作之间的逻辑关系;
(4) 根节点到除根节点以外的任意一个节点都至少存在一条路线;
(5) 图中不存在环。
则称这个有向图为项目管理图模型。
条件(1)、(2)和(3)实际是采用单代号网络图[10]的形式来表示各项工作之间相互依赖、相互制约的关系。采用这种表示形式的网络图同时也是图论中所描述的有向图中的一种,对于满足条件(4)的有向图,可以很容易的证明该有向图是弱连通图[9],同时由于条件(5),图中不存在环,因此项目管理有向图并不是强连通图[8]。
3. 一种新的广度优先关键路线生成算法
3.1. 回溯最大路线算法
为实现生成关键路线的算法,给出一个辅助算法即回溯最大路线算法,实现从根节点到任意给定节点最大路线的确定,算法流程图如图3所示。
该算法采用伪代码描述,并使用了数据结构中的队列,队列是一种动态集合,实现了先进先出(first_in, first_out, FIFO)策略[11]。其中 表示将元素i插入队列Q中,
表示将元素i插入队列Q中,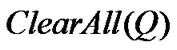 表示删除队列中
表示删除队列中
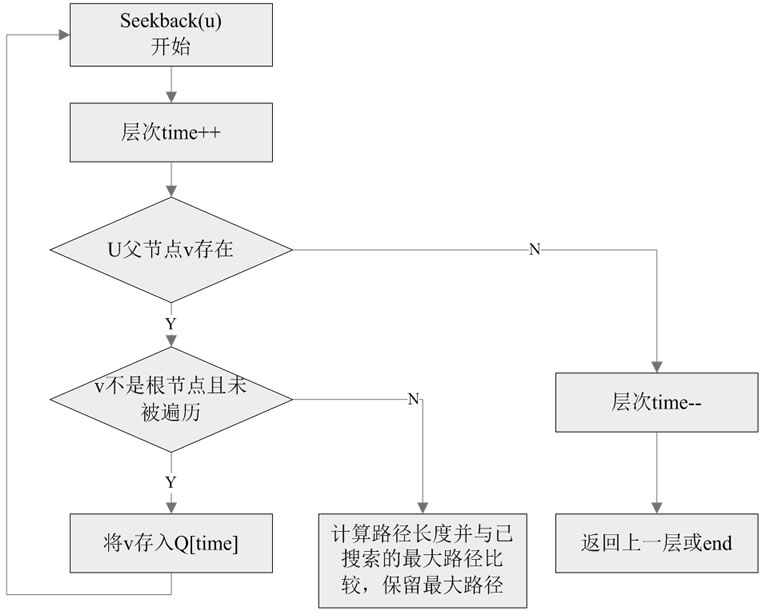
Figure 3. The flow chart of the backtracking maximum path algorithm
图3. 回溯最大路径算法流程图
所有元素。定义数组![]() 用于存储路线节点信息,全局变量
用于存储路线节点信息,全局变量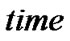 用于存储距目标节点层次,
用于存储距目标节点层次,![]() 用于存储当前最大路线值,初值为0,队列
用于存储当前最大路线值,初值为0,队列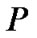 用于存储最大路线,算法名称
用于存储最大路线,算法名称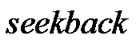 ,并且
,并且![]() ,
,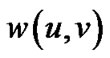 表示边
表示边 的权值。
的权值。
输入:目标节点![]() 。
。
输出:队列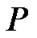 和最大路线值
和最大路线值![]() (
(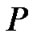 存储了从根节点
存储了从根节点![]() 到目标节点
到目标节点![]() 的最大路线节点,存储了从根节点
的最大路线节点,存储了从根节点![]() 到目标节点
到目标节点![]() 的最大路线值)。
的最大路线值)。

3.2. 广度优先最大路线生成算法
回溯最大路线算法能够输出根节点到任意节点之间的最大路线,那么只要能够遍历整个图,对图模型中的每一个节点都调用该算法,就可以计算出每一个节点到根节点的最大路线了,该算法的流程图如图4所示。
本文算法采用广度优先遍历算法[12-14],伪代码采用MIT教授Thomas H. Cormen等推荐的形式,实现关键路线的自动生成。对于任意满足前面条件的图模型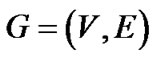 ,对于任意节点
,对于任意节点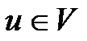 ,其色彩存储于变量
,其色彩存储于变量 中,
中,![]() 的父节点存于
的父节点存于![]() 中,如果
中,如果![]() 没有父节点,则
没有父节点,则![]() 。源顶点
。源顶点![]() 和
和![]() 之间距离存于变量
之间距离存于变量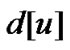 中,且
中,且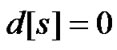 。
。
输入:有向图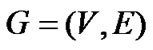 。
。
输入:数组![]() 和
和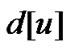 ,
, (
(![]() 存储任意节点
存储任意节点![]() 的父节点,
的父节点,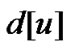 存储根节点
存储根节点![]() 到节点
到节点![]() 的最大距离)。
的最大距离)。

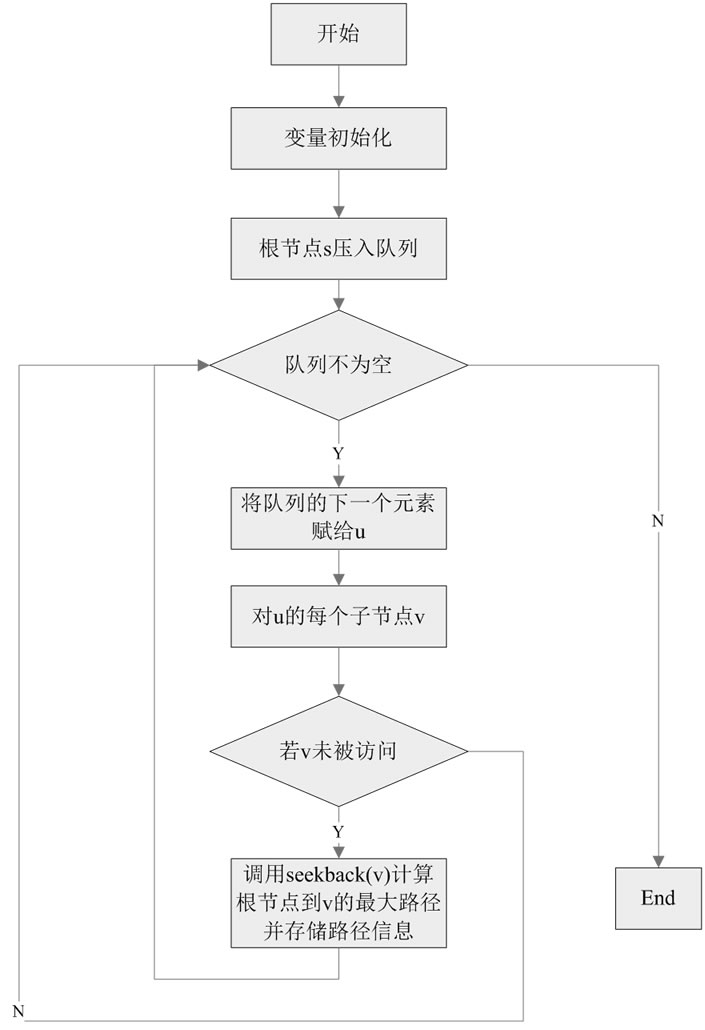
Figure 4. The flow chart of the maximum path spanning tree algorithm
图4. 广度优先最大路径生成算法流程图
3.3. 算法的优化
项目管理图模型的最大路线有两个很重要的性质,通过这两个性质可以实现对算法的优化,提高算法的执行效率。
性质2.1 对于一个项目管理图模型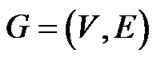 ,若从根节点
,若从根节点![]() 到节点
到节点![]() 的最大路线为
的最大路线为 ,则该路线上任意一个节点
,则该路线上任意一个节点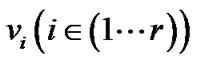 ,路线
,路线 是
是![]() 到
到![]() 的最大路线。
的最大路线。
证明:设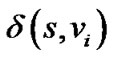 表示
表示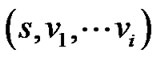 的长度。
的长度。
假设路线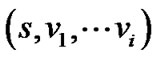 不是
不是![]() 到
到![]() 的最大路线,则存在另一条路线
的最大路线,则存在另一条路线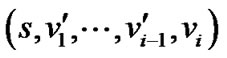 (该路线的长度用
(该路线的长度用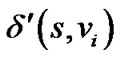 表示),使得
表示),使得 成立。
成立。
假设 表示路线
表示路线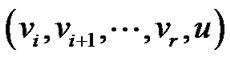 的长度。则有下式成立:
的长度。则有下式成立:

故路线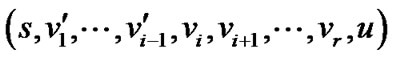 比
比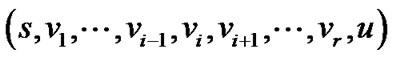 大,
大,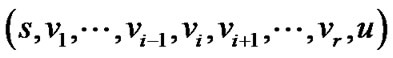 不是最大路线,与已知条件矛盾,故假设不成立,
不是最大路线,与已知条件矛盾,故假设不成立,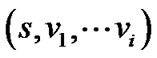 是
是![]() 到
到![]() 的最大路线。
的最大路线。
根据性质2.1,采用最大路线回溯算法确立根节点到目标节点的最大路线后,该路线上的每一个节点的最大路线就完全确定了,当采用广度优先遍历到该节点时,不需要对该节点进行重复回溯计算,2.2节算法18~27实现将已确定的路径上所有节点的路径信息存储的功能。
性质2.2 已知有向图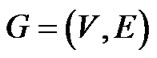 存在从节点
存在从节点![]() 到目标节点
到目标节点![]() 的路线,且从根节点
的路线,且从根节点![]() 到节点
到节点![]() 的最大路线为
的最大路线为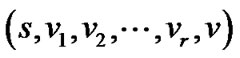 ,则从
,则从![]() 经过
经过![]() 到达目标节点
到达目标节点![]() 的最大路线必然经过路线
的最大路线必然经过路线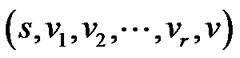 。
。
证明:设 表示路线
表示路线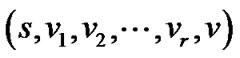 的长度。
的长度。![]() 到目标节点的最大路线为
到目标节点的最大路线为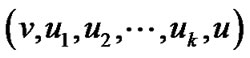 ,其长度为
,其长度为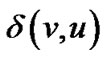 。则
。则
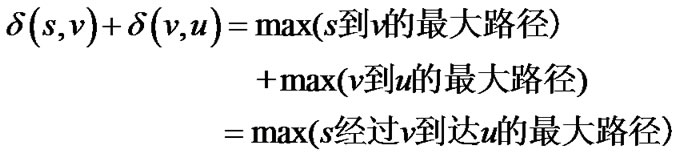
因此路线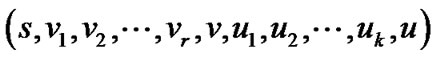 为
为![]() 经过
经过![]() 到达
到达![]() 的最大路径。
的最大路径。
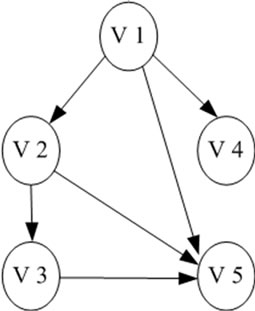
根据性质2.2,采用回溯最大路线算法时,如果回溯至某个节点且该节点到根节点的最大路线已经确定,那么不需要再回到根节点就可以知道从根节点经过该节点到达目标节点的最大路线,再和不经过该节点的路线进行比较就可以求出根节点到目标节点的最大路线。假设图5所示的图模型是某项目的网络图模型,并且满足前面定义的项目管理图模型的条件,如果目标节点为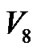 ,并且节点
,并且节点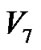 到根节点
到根节点 的最大路线已经确定(
的最大路线已经确定(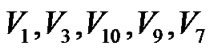 ),那么由
),那么由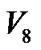 回溯到
回溯到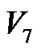 时,就没有必要再继续回溯,从根节点
时,就没有必要再继续回溯,从根节点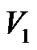 经过
经过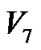 达到目标节点
达到目标节点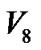 的最大路径为
的最大路径为 。因此可以在回溯最大路线算法的第3行对判断条件进行修改:
。因此可以在回溯最大路线算法的第3行对判断条件进行修改:

结合性质2.1,在每找出一条路线后,就确定了该路线上所有点到根节点的最大路线,将该节点的父节点及最大路线进行存储,并标记,这样就不用重复计算,每个节点只计算一次。同时,由于项目管理任务的前后逻辑性比较强,因此采用广度优先遍历可以最大程度的保证目标节点的父节点到根节点的最大路线被确定,进一步提高算法效率。
4. 结果仿真
对于图5中所示的图模型,采用基于广度优先遍历的关键路线生成树算法(JAVA实现)如图6所示,得到该计划图的关键路线为v1-v3-v5-v2-v6-v8,同时还可以得到根节点到任意节点的最大路径,这些最大路径信息对于项目优化具有重大意义。
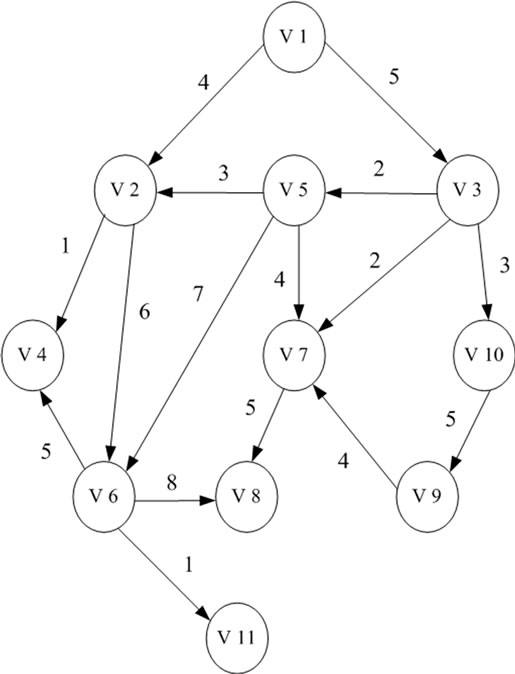
Figure 5. Example of project management graph model
图5. 项目管理图模型示例
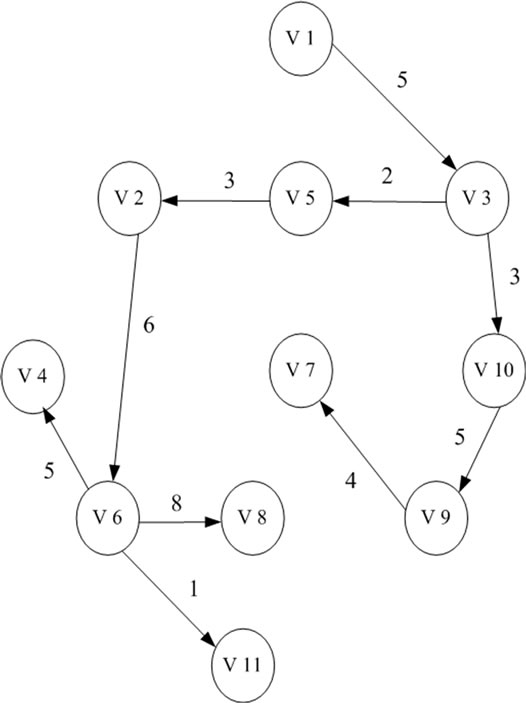
Figure 6. Result of critical path spanning tree algorithm
图6. 采用关键路线生成算法后生成树结果
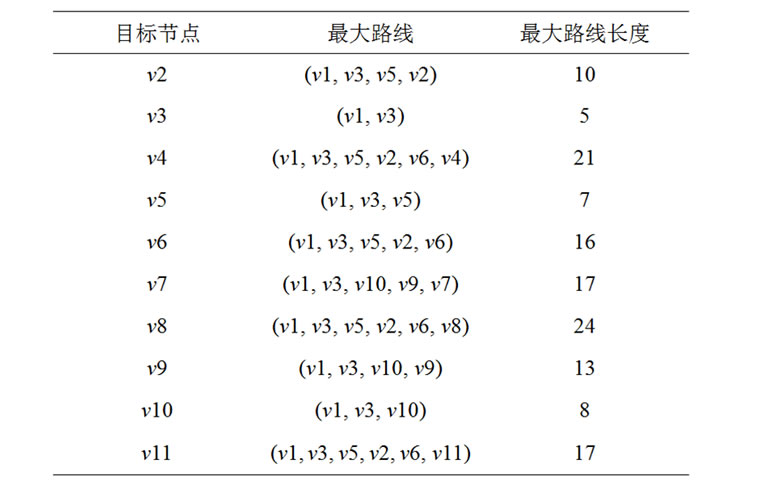
Table 1. Maximum path of the graph model in Figure 3
表1. 原图模型最大路线枚举表
对于原图模型,通过枚举计算根节点到每个节点的最大路线,如表1所示。通过表可以得出原图模型的最大路径为v1-v3-v5-v2-v6-v8,算法计算结果与实际情况完全吻合。
5. 结论
由仿真结果可见,本文所定义的项目管理图模型及关键路线生成算法为解决关键路线的确定问题提供了一种新的方法。算法采用伪代码的形式,可以方便的转换为各种常用语言比如C、Java、C++,并方便的应用到实际中。另外,本算法在保留了原图模型关键路线的同时,完成了对图模型的剪枝,生成了一棵保留了根节点到任意节点最大路线信息的树。通过生成的树不仅可以轻易找出关键路线,更能够方便的找出根节点到任意节点的关键路线,便于对复杂的任务进行关键节点控制。由于树比图更易于在计算机中实现,因此生成的树对于通过计算机技术实现网络计划技术的电子化、流程化管理也具有重要的意义。
参考文献 (References)
[1] 乞建勋, 李星梅, 王强. 等效子网络构建的理论与方法[J]. 管理科学学报, 2010, 13(1): 40-43.
[2] 李宁, 吴之明. 网络计划技术的新发展——项目关键链管理(CCPM) [J]. Highway, 2002, 10: 83-86.
[3] 刘芳, 王玲. 基于动态规划思想求解关键路径的算法[J]. 计算机应用, 2006, 26(6): 1440-1442.
[4] 徐志勇, 张开富, 李正兰, 姜寿山. 一种面向航空产品的分级网络计划方法[J]. 计算机集成制造系统, 2006, 12(5): 24-28.
[5] 刘秀凤. 网络计划技术优化方法在建筑工程施工管理中的应用研究[D]. 天津大学, 2008: 45-50.
[6] 师海忠. 有向图语言[J]. 计算机工程与应用, 2011, 22: 53-56.
[7] T. H. Cormen, C. E. Leiserson, R. L. Rivest, et al. Introduction to algorithms [M]. 北京: 机械工业出版社, 2006.
[8] D. West. Introduction to graph theory [M]. 北京: 机械工业出版社, 2006.
[9] J. 邦詹森 [丹], G. 古廷 [英]. 有向图的理论、算法及其应用[M]. 北京: 科学出版社, 2007: 155-158.
[10] 褚春超,郑丕谔, 邬旺. 单代号网络图的计算机辅助生成研究[J]. 计算机辅助设计与图形学学报, 2005, 17(9): 2133-2137.
[11] R. E. Tarjan. Data structures and network algorithms. Philadelphia: Society for Industrial and Applied Mathematics, 1983: 234-238.
[12] S. Even. Graph algorithms. New York: Computer Science Press, 1979: 23-28.
[13] A. Datta. Efficient graph algorithms on a linear array with a reconfigurable pipelined bus system. 15th International Proceedings of Parallel and Distributed Processing Symposium, 2001: 234-238.
[14] V. Kumar, E. J. Schwabe. Improved algorithms and data structures for solving graph problems in external memory. Parallel and Distributed Processing, 1996: 132-135.
NOTES
*基金项目:北京市教育委员会重点学科共建项目资助(xk10008 0537)。