Computer Science and Application
Vol.4 No.03(2014), Article ID:13291,6 pages
DOI:10.12677/CSA.2014.43009
Spanning Trees in a Class of Four Regular Small World Network
1Department of Mathematics, Qinghai Normal University, Xining
2Department of Computer Science, Qinghai Normal University, Xining
Email: jhs1989@163.com, h.x.zhao@163.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jan. 31st, 2014; revised: Feb. 26th, 2014; accepted: Mar. 10th, 2014
ABSTRACT
Spanning tree is an important quantity characterizing the reliability of a network; however, explicitly determining the number of spanning trees in networks is a theoretical challenge. In this paper, we present a class of four regular network model with small world phenomenon. We introduce the concept and evolving process and determine the relevant topological characteristics of the four regular network, such as diameter and clustering coefficient. We give a calculation method of number of spanning trees in such four regular network and derive the formulas and the entropy of number of spanning trees. We find that the entropy of spanning trees in the studied network is in sharp contrast to other small world with the same average degree, of which the entropy is less than the studied network. Thus, the number of spanning trees in such four regular network is more than that of other self-similar networks.
Keywords:Complex Network; Four Regular Network; Spanning Tree

一类四正则小世界网络的生成树数目的算法
贾环身1,赵海兴2
1青海师范大学数学系,西宁
2青海师范大学计算机学院,西宁
Email: jhs1989@163.com, h.x.zhao@163.com
收稿日期:2014年1月31日;修回日期:2014年2月26日;录用日期:2014年3月10日

摘 要
生成树是表征网络结构性质的一个重要物理量,然而精确地确定网络上的生成树数目是一个巨大的理论挑战。本文提出了一个四正则小世界网络模型。介绍了其概念及演化过程,详细计算了四正则图的相关拓扑特性,例如直径、聚类系数等。给出了此类四正则网络的生成树数目计算方法,得出生成树数目公式及熵。研究发现,所研究网络的生成树的熵与具有相同平均度的其他网络形成了鲜明的对比,因为后者的生成树的熵小于所研究网络。因此,这一四正则小世界网络上的生成树数目比其他具有自相似结构网络生成树的数目要多。
关键词
复杂网络;四正则网络;生成树

1. 引言
复杂网络已成为学术界研究的一个热点,许多现实世界中的网络都具有小世界效应,例如:电力网络、生物网络、交通网络、社会关系网络。一个网络具有小世界效应是指该网络具有较小的平均路径长度和较大的聚类系数这两个主要的属性,这里较小的平均路径长度是指网络的平均路径长度按照网络的阶的对数形式增长。
作为网络的另外一个重要的结构性质,网络中生成树数目的计算在数学、物理和其他学科里是一个基本的问题。生成树与网络的诸多方面有着紧密的联系[1] [2] ,包括可靠性[3] 、最优同步[4] 、运输[5] 、随机游走[6] [7] 等。例如:一个网络的生成树数目与网络中两个节点之间的有效电阻密切相关[8] ,并且还可以反过来决定两节点之间的平均首达时间;作为随机游走的一个基本量,生成树数目在不同理论和应用领域都有广泛的应用。另一方面,对于一个连通网络,在保持节点数不变的情况下,其生成树数目最大的结构网络具有最好的同步能力。最近,网络中的生成树一直是许多研究关注的焦点。许多文章中已经研究了特定网络中生成树数目,例如,Sierpinski网络[9] ,E-R随机图[10] 以及章忠志等人给出的分形无标度网络[2] ,伪分形无标度网络[11] ,小世界法雷网络[12] ,在2013年,作为所提出的计算生成树数目的新方法的算例,赵海兴等人计算出了文献[13] [14] 中的模型的生成树数目.这些研究说明了不同网络结构中的生成树有不同的影响。
本文提出了一类具有小世界现象的四正则网络并且得到了其相应的拓扑特性,例如直径、聚类系数。结果表明我们的模型具有离散指数度分布、高聚类系数、较小的直径,满足小世界网络的主要特性;给出了此类四正则网络的生成树数目的计算方法并得到了相应的公式,根据生成树数目确定了生成树的熵。
2. 网络生成的迭代算法
正则图是每个顶点的度相同的图[15] 。若每个顶点的度均为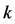 ,称为
,称为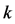 -正则图。通过迭代的方法构造了一类四正则图。为了正确计算
-正则图。通过迭代的方法构造了一类四正则图。为了正确计算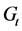 的生成树数目,首先构建一个新模型
的生成树数目,首先构建一个新模型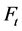 如图1、2所示,用
如图1、2所示,用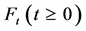 来表示经过
来表示经过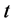 步后的网络,网络
步后的网络,网络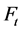 的生成算法如下:当
的生成算法如下:当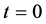 时的初始网络
时的初始网络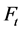 是一个四个节点连接三条边的三叉树,当
是一个四个节点连接三条边的三叉树,当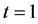 时网络
时网络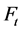 是由两个三叉树粘贴而成,使得最底层的每个叶子节点的度为4,对于
是由两个三叉树粘贴而成,使得最底层的每个叶子节点的度为4,对于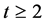 ,
,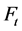 通过如下的方式得到:对
通过如下的方式得到:对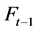 中在
中在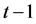 步生成的三叉树的每个叶子节点再生出三个叶子节点,然后复制这个三叉树,粘贴这两个三叉树的最底层叶子节点并使得它们的度为4(如图1)。计算得到了网络
步生成的三叉树的每个叶子节点再生出三个叶子节点,然后复制这个三叉树,粘贴这两个三叉树的最底层叶子节点并使得它们的度为4(如图1)。计算得到了网络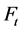 的总
的总
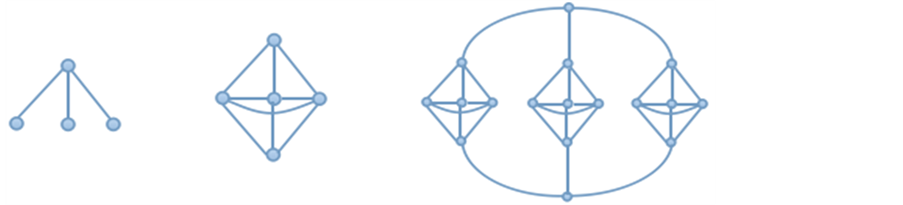
t = 0 t = 1 t=2
Figure 1. Construction of Ft, showing the first three steps of the iterative process
图1. Ft的前三步迭代构造
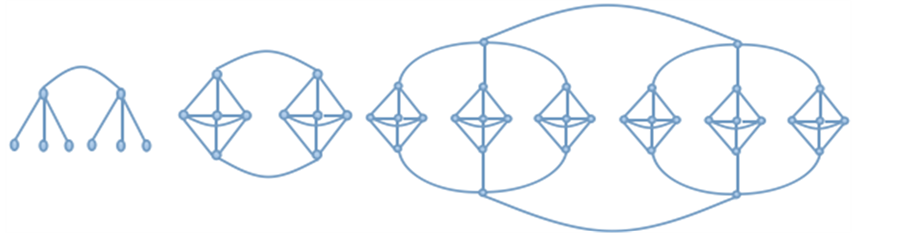
t = 0 t = 1 t=2
Figure 2. Construction of Gt, showing the first three steps of the iterative process
图2. Gt的前三步迭构造
点数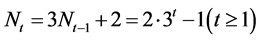 和总边数
和总边数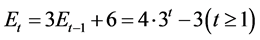 。
。
本文所研究的四正则网络模型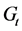 是由两条边连接两个
是由两条边连接两个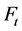 构成的(如图2)。并计算得到了
构成的(如图2)。并计算得到了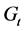 的总点数
的总点数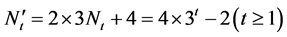 和总边数
和总边数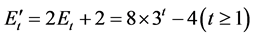 。
。
3. 拓扑特性
3.1. 直径(Diameter)
直径定义为网络中任意两个顶点间最小距离的最大值,它是反映网络最大传递延迟的属性。小的直径与小世界网络的概念是一致的,这里用直径代替平均路径长度来说明网络的小世界特性。用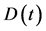 表示本网络模型的时间步
表示本网络模型的时间步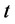 时的直径。由图2知,
时的直径。由图2知,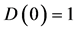 ,
,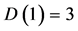 ,在接下来的每一迭代步
,在接下来的每一迭代步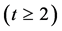 中,直径随着新点的增加而增加.网络的直径满足如下公式:
中,直径随着新点的增加而增加.网络的直径满足如下公式:
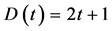
用归纳法可证明公式成立,并且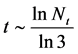 。
。
因此直径随着节点数的增加呈对数形式增长,所以该四正则网络满足小世界网络特性。
3.2. 聚类系数(Clustering Coefficient)
聚类系数是用来衡量一个复杂网络的集团化程度。节点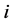 的聚集系数
的聚集系数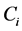 描述的是网络中与该节点直接相连的节点之间的连接关系,即与该节点直接相邻的节点间实际存在的边数目占最大可能存在的边数
描述的是网络中与该节点直接相连的节点之间的连接关系,即与该节点直接相邻的节点间实际存在的边数目占最大可能存在的边数
的比例,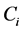 的表达式为
的表达式为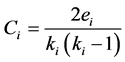 ,式中
,式中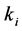 表示节点
表示节点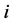 的度,
的度,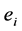 表示节点
表示节点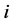 的邻接节点之间实际存在的边数。网络的聚集系数
的邻接节点之间实际存在的边数。网络的聚集系数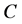 为所有节点聚集系数的算术平均值,即
为所有节点聚集系数的算术平均值,即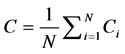 ,其中
,其中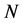 为网络的阶。在
为网络的阶。在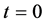 步,
步,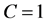 。在接下来的每一步
。在接下来的每一步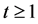 ,都有
,都有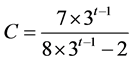 。
。
显然,当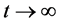 时,
时,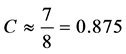 ,具有较高的聚类系数,满足小世界特性。
,具有较高的聚类系数,满足小世界特性。
4. 生成树数目(Spanning Trees)
生成树 是一个连通图
是一个连通图 的一个极小连通子图,包含
的一个极小连通子图,包含 的所有
的所有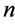 个顶点,有
个顶点,有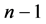 条边的连通图。若
条边的连通图。若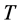 为森林,则称它为
为森林,则称它为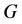 的一个生成森林。我们找出了
的一个生成森林。我们找出了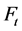 和
和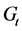 的关系(如图3)。假设
的关系(如图3)。假设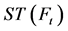 表示在
表示在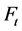 中第
中第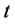 步时的生成树数目,
步时的生成树数目,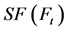 表示在
表示在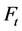 中第
中第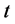 步时具有两个分支的生成森林数目,那么通过计算
步时具有两个分支的生成森林数目,那么通过计算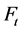 的生成树数目来求得原模型
的生成树数目来求得原模型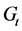 的生成树数目,他们的关系如公式(1):
的生成树数目,他们的关系如公式(1):
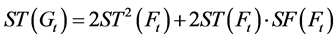 (1)
(1)
由图3和图4容易看出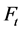 在第
在第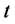 步时的生成树数目是通过迭代的方法由
步时的生成树数目是通过迭代的方法由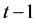 步得到的,并且
步得到的,并且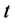 步的生成树是由
步的生成树是由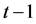 步生成树和生成森林共同构成的,
步生成树和生成森林共同构成的,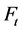 有以下几种情形:
有以下几种情形:
由图5可以看出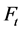 的包含两个分支的生成森林有以下几种情形:
的包含两个分支的生成森林有以下几种情形:
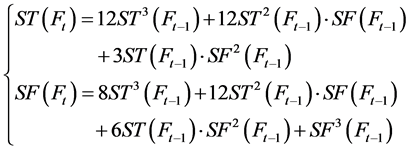 (2)
(2)
其中: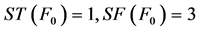 。
。
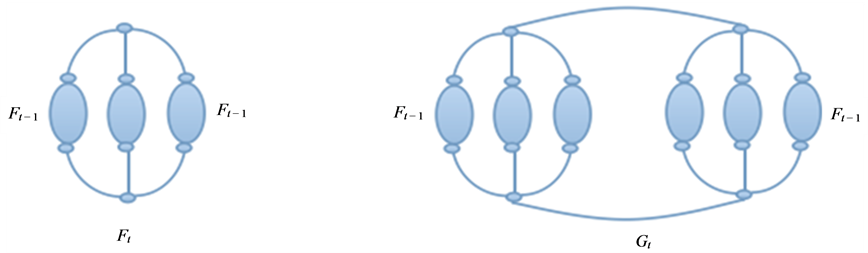
Figure 3. The network model Ft and Gt at step t
图3. t步时的网络Ft和Gt
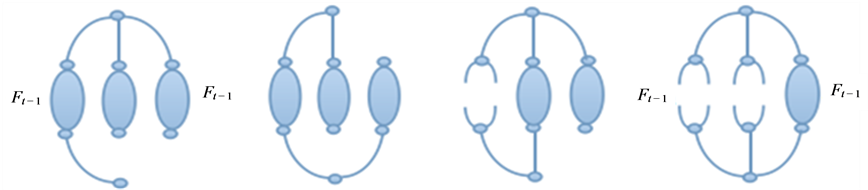
Figure 4. The number of spanning trees of Ft
图4. Ft的生成树数目;
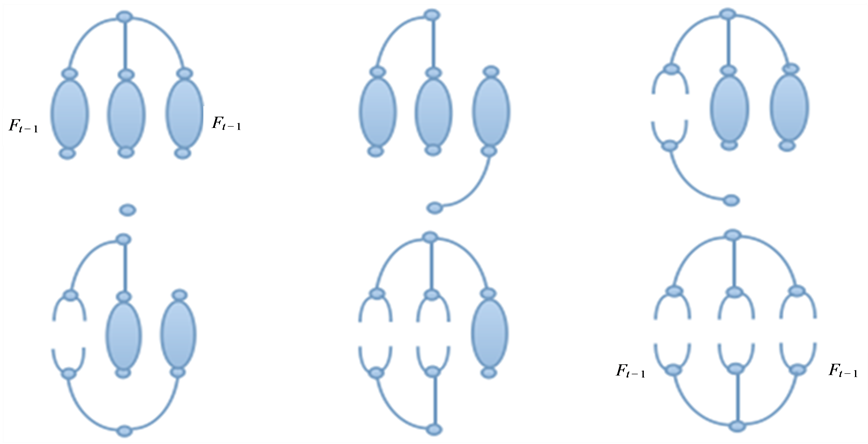
Figure 5. The number of spanning forests with two components of Ft
图5. Ft中具有两个分支的生成森林数目
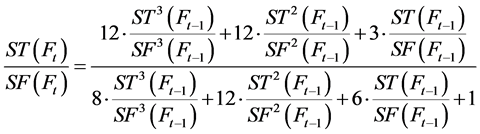
令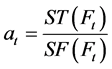 ,则
,则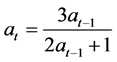 ,其中
,其中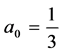 。
。
因此可得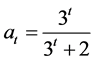 。
。
注意到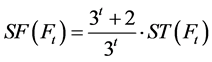 ,代入
,代入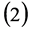 式得:
式得:
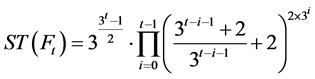 (3)
(3)
同理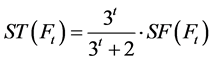 ,可得:
,可得:
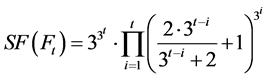 (4)
(4)
根据(3),(4)式可推出公式(1)得到 的生成树数目:
的生成树数目:
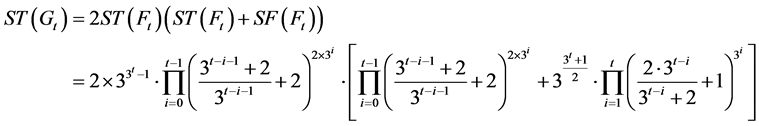
则通过生成树数目计算出了 的生成树的熵:
的生成树的熵:
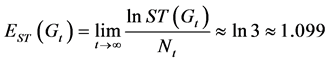
我们计算出了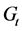 的生成树树数目的精确解,以及该网络生成树的熵。通过所得到的不同网络生成树的结果,我们将
的生成树树数目的精确解,以及该网络生成树的熵。通过所得到的不同网络生成树的结果,我们将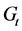 的生成树数目的熵与其他具有相同平均度的网络进行比较。文献[2] 中平均度为4的分形无标度网络的生成树的熵为
的生成树数目的熵与其他具有相同平均度的网络进行比较。文献[2] 中平均度为4的分形无标度网络的生成树的熵为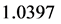 ,文献[11] 中伪分形无标度网络的生成树的熵为0.8959,二维Sierpinski网络的生成树的熵为
,文献[11] 中伪分形无标度网络的生成树的熵为0.8959,二维Sierpinski网络的生成树的熵为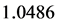 [9] ,它们都于小于1.099。因此,该小世界正则网络上的生成树数目比其他具有相同平均度网络的生成树的数目较大.这说明了两个网络生成树存在差别的主要原因在于它们的结构差异。
[9] ,它们都于小于1.099。因此,该小世界正则网络上的生成树数目比其他具有相同平均度网络的生成树的数目较大.这说明了两个网络生成树存在差别的主要原因在于它们的结构差异。
5. 总结
本文用迭代的方法构造了一类具有小世界效应的四正则网络模型,分析并得到了网络包括直径和聚类系数的主要拓扑特性。生成树作为网络结构性质的一个重要物理量,我们给出了此类四正则网络的生成树数目计算方法,得出生成树数目公式及熵。研究发现,所研究网络的生成树的熵与具有相同平均度的其他网络形成了鲜明的对比,这一四正则小世界网络上的生成树数目比其他具有自相似结构网络生成树的数目要多,也说明了不同网络之间的结构差异,我们给出的生成树数目的计算方法也可以应用到其他自相似网络上。
基金项目
科技部973专项(No.2010CB334708)、国家自然基金项目(No.61164005)、教育部长江学者与创新团队支持计划(No.IRT1068)、青海省自然基金项目(No.2012-Z-943)。
参考文献 (References)
- [1] Zhang, Z.Z., Gao, S.Y., Chen, L.C., Zhou, S.G., Zhang, H.J. and Guan, J.H. (2010) Mapping Koch curves into scalefree small-world networks. Journal of Physics A: Mathematical and Theoretical, 43, Article ID: 395101.
- [2] Zhang, Z.Z., Liu, H.X., Wu, B. and Zou, T. (2011) Spanning trees in a fractal scale-free lattice. Physical Review E, 83, Article ID: 016116.
- [3] Boesch, F.T. (1986) On unreliabillity polynomials and graph connectivity in reliable network synthesis. Journal of Graph Theory, 10, 339-352.
- [4] Nishikawa, T. and Motter, A.E. (2006) Synchronization is optimal in non-diagonalizable networks. Physical Review E, 73, Article ID: 065106.
- [5] Noh, J.D. and Rieger, H. (2003) Random walks on complex networks. Physical Review, 92, Article ID: 118701.
- [6] Dhar, D. and Dhar, A. (1997) Distribution of sizes of erased loops for loop-erased random walks. Physical Review E, 55, 2093.
- [7] Zhang, Z.Z., Shan, T. and Chen, G.R. (2013) Random walks on weighted networks. Physical Review E, 87, Article ID: 012112.
- [8] Bapat, R.B. (1999) Resistance distance in graphs. The Mathematics Student, 68, 87-98.
- [9] Chang, S.C., Chen, L.C. and Yang, W.S. (2007) Spanning Trees on the Sierpinski Gasket. Journal of Physics, 126, 649.
- [10] Lyons, R., Peled, R. and Schramm, O. (2008) Growth of the number of spanning trees of the Erdős-Rényi giant component. Combinatorics, Probability and Computing, 17, 711.
- [11] Zhang, Z.Z., Liu, H.X., Wu, B. and Zhou, S.G. (2010) Enumeration of spanning tree in a pseudofractal scale-free web. Europhysics Letters, 90, Article ID: 68002.
- [12] Zhang, Z.Z., Wu, B. and Lin, Y. (2012) Counting spanning trees in a small-world Farey graph. Physica A, 391, 3342- 3349.
- [13] Hu, G.N., Xiao, Y.Z., Jia, H.S. and Zhao, H.X. (2013) A new class of the planar networks with high clustering and high entropy. Abstract and Applied Analysis, 2013, Article ID: 795682.
- [14] Xiao, Y.Z. and Zhao, H.X. (2013) New method for counting the number of spanning trees in a two -tree network. Physica A: Statistical Mechanics and Its Applications, 392, 4576-4583.
- [15] Bondy, J.A. and Murty, U.S.R. (1976) Graph theory with application. American Elsevier, New York, 10-12.