Smart Grid
Vol.06 No.02(2016), Article ID:17290,9
pages
10.12677/SG.2016.62006
Influence of Sampling Period on the Accuracy of Single Phase to Ground Fault in Transmission Line
Xiangfei Meng, Yijun Sun, Hongmin Hao, Jian Wang
College of Electrical and Electronic Engineering, Shandong University of Technology, Zibo Shandong

Received: Mar. 14th, 2016; accepted: Mar. 29th, 2016; published: Apr. 1st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
We analyze the basic principle of power frequency fault location of single-phase to ground fault in three-phase system of transmission line and use PSCAD/EMTDC simulation software to build the transmission line distributed parameter model. According to the transmission line single-phase grounding short circuit fault simulation, we use the Fourier algorithm to extract cycles of failure and calculate the voltage and current of power frequency to fault location, which is based on power frequency component of single end fault distance measurement principle. And current power frequency is analyzed by using the Fourier algorithm. Based on the real time fault data collected by the recorder in the single phase to ground fault in the small sand 110 KV large Xiapu Fujian wind line, the influence of the sampling period on the ranging results is verified. It can be used for referencing in the selection of sampling period when using power frequency to carry out fault location.
Keywords:Transmission Line, Simulation Modeling, Fault Location, Case Study

输电线路发生单相接地短路后采样周期对测距精度的影响
孟祥飞,孙懿君,郝洪民,王建
山东理工大学电气与电子工程学院,山东 淄博

收稿日期:2016年3月14日;录用日期:2016年3月29日;发布日期:2016年4月1日

摘 要
本文分析了输电线路三相系统发生单相接地短路故障时工频测距的基本原理。选用PSCAD/EMTDC仿真软件搭建输电线路分布参数模型,针对输电线路发生单相接地短路故障进行仿真,使用傅立叶算法对故障周期进行提取并计算电压电流工频量,利用基于工频分量的单端故障测距原理进行故障测距。分析利用傅立叶算法在提取电压电流工频量时选取不同采样周期对测距精度的影响。借助福建霞浦小沙110 KV大京风电线发生单相接地短路故障时,录波器采集到的实时故障数据,验证采样周期对测距结果的影响。对利用工频量进行故障测距时采样周期的选取有一定的借鉴意义。
关键词 :输电线路,仿真建模,故障测距,实例分析

1. 引言
输电线路是电力系统的重要组成部分,有着输送电能的重要作用,同时因为我国复杂多变的自然条件,致使输电线路很容易发生故障,当故障发生后,准确及时的对故障发生点进行定位,对整个电力系统的安全稳定运行有着十分积极的作用 [1] 。
故障测距的方法按测距原理可分为行波法和故障分析法,根据测距所需的信息来源可分为单端量法和两端量法 [2] 。基于工频分量的单端测距算法仅使用测量端测到的电压、电流和必要的系统参数来计算故障距离。由于只使用本侧信息,实现起来简单方便 [3] 。但是基于工频分量的测距算法因故障支路过渡电阻的影响及长距离输电线路中存在的分布电容,会影响测距精度,文献 [4] 提出了一种利用保护安装处负序电流相位代替故障点处故障电流相位的方法来消除过渡电阻的影响,文献 [5] 提出了一种能在微机保护中实现消除过渡电阻影响的新算法。文献 [6] 提出一种变频电阻测量方法,选择两个合适频率的交流方波施加于由电极组成的分压电路上,通过解方程组求出分压电路时间常数f,然后求得被测电阻值,这种方法有效消除了电容对电阻测量精度的影响。除了过渡电阻及分布电容对测距精度的影响外,在利用工频量进行测距是采样周期的选取同样会影响测距精度。
基于上述问题,本文通过搭建输电线路分布参数模型,对线路发生单相接地短路故障进行仿真,通过傅立叶算法对仿真波形进行电压电流工频量提取,分别选取不同周期进行测距,分析不同采样周期对测距精度的影响。同时以福建霞浦小沙110 KV大京风电线发生单相接地短路故障为例,对线路发生故障时录波器采集的数据进行分析,利用傅立叶算法对不同采样周期求取故障点距离。对输电线路发生故障后采样周期的选取具有借鉴意义。
2. 测距原理及算法介绍
2.1. 单相接地短路故障工频测距原理
图1为三相系统发生单相接地短路故障时的电气示意图,假设输电线路发生A相接地短路故障,故障点F处的边界条件为:
 (1-1)
(1-1)
其中: 为A相故障电压,
为A相故障电压, 为A相故障电流。
为A相故障电流。
序边界条件为:
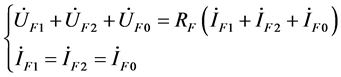 (1-2)
(1-2)
其中: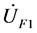 、
、 和
和 为故障支路正序、负序和零序电压,
为故障支路正序、负序和零序电压, 、
、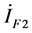 和
和 为故障支路正序、负序和零序电流。
为故障支路正序、负序和零序电流。
从以上两式可以看出三序网为串联关系,如图2所示。

Figure 1. Double end power system electrical schematic diagram
图1. 双端电源系统电气示意图

Figure 2. Transmission line single-phase grounding fault occurs in three sequence network
图2. 输电线路发生单相接地故障时三序网
当输电线路发生单相接地短路故障时:三个序网的电压之和为零、三个序网的电流是相等的。故障支路电流可以表示为:
 (1-3)
(1-3)
根据图1,图2,以A相为基准分别列出列出其故障后的三序网络方程:
 (1-4)
(1-4)
其中: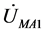 、
、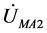 和
和 分别是故障后在M端所测得的A相正序、负序和零序电压,
分别是故障后在M端所测得的A相正序、负序和零序电压, 、
、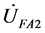 和
和 分别是故障支路的正序、负序和零序电压,
分别是故障支路的正序、负序和零序电压,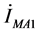 、
、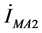 和
和 分别是故障后在M端所测得的A相正序、负序和零序电流。
分别是故障后在M端所测得的A相正序、负序和零序电流。
将三个序网方程组相加,就得到了A相的电压与电流的关系:
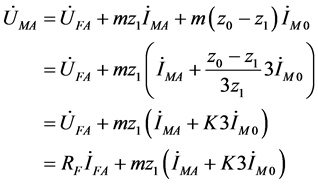 (1-5)
(1-5)
其中: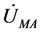 和
和 分别为故障时在M端测得的A相电压和电流,
分别为故障时在M端测得的A相电压和电流,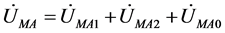 ,
, ,
,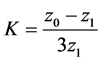 为线路的零序补偿系数。
为线路的零序补偿系数。
整理可得一般式:
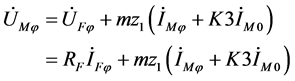 (1-6)
(1-6)
其中: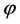 代表三相中任意一相。
代表三相中任意一相。
因过渡电阻呈电阻性,对上式取虚部,为消去故障支路电流,两边同乘共轭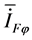 得:
得:
 (1-7)
(1-7)
根据故障分量基本理论 [7] ,故障支路电流 可以用测量端故障电流的零序分量来代替,即
可以用测量端故障电流的零序分量来代替,即
 ,
, (1-8)
(1-8)
将式(1-8)代入式(1-7)得:
 (1-9)
(1-9)
整理得故障距离:
 (1-10)
(1-10)
2.2. 傅立叶算法
利用傅立叶算法求取母线电压有效值及故障线路电流有效值。傅里叶算法的基本思路自傅立叶级数。假定被采样的模拟信号x(t)随时间周期性变化,则可以表示为
 (1-11)
(1-11)
其中 ,
, ,N为一个周期内的采样点数,假设基本频率为工频50 Hz,采样频率为3200 Hz,则一个周期有3200/50 = 64个点。
,N为一个周期内的采样点数,假设基本频率为工频50 Hz,采样频率为3200 Hz,则一个周期有3200/50 = 64个点。
在微机保护中采用离散算法:
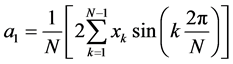 ,
, (1-12)
(1-12)
求出a,b后可以求得相应的电压、电流有效值。然后利用阻抗法,根据求得的测量端电压、电流值及线路单位长度的阻抗等系统参数进行测距。
3. 仿真验证
3.1. 仿真模型的构建
本文利用仿真软件PSCAD搭建一条额定电压为500 kV的输电线路作为仿真模型 [8] ,系统电压等级为500 kV,频率为工频50 Hz,分布参数为:

仿真模型如图3所示。
其中电源选取R-L-C电源,在选取的同时设置电源频率50 Hz、相位0˚、线路额定电压500 kV及电压爬升时间0.05 S,故障模块可选择故障类型,如单相接地短路、两相短路、两相短路接地等,因实际线路中绝大多数故障类型为单相接地短路,所以此处设置故障类型为A相接地短路。模型搭建完成后,设置仿真步长1000 Hz,仿真时间0.5 S,故障发生于0.2 S,持续时间0.15 S。
3.2. 仿真结果
以线路发生A相接地短路为例,仿真波形如图4所示。
在PSCAD中,设置故障距离为20 km,过渡电阻设置为10 Ω,运行仿真,将仿真结果导入Matlab,利用傅立叶算法分别对故障发生后一个周期及断路器动作前一个周期进行数据采样,获取电压电流的工频量,然后利用基于工频分量的单端故障测距原理进行测距,所得结果见表1。
为分析采样周期的选择对测距精度的影响,现将故障距离分别设置为10 km、15 km、25 km、30 km、50 km、70 km,对故障发生后一个周期及断路器动作前一个周期进行数据采样,利用Matlab对数据处理的方法与故障距离设置在20 km处相同,测距结果如表2所示。
由表2可以看出,在过渡电阻、线路参数等不变,仅改变故障距离时,利用故障发生后一个周期的采样数据进行测距,无法较为准确的获得故障发生后电压电流的工频量,其测距精度要小于利用断路器动作前一个周期的采样数据所求得的故障距离。

Figure 3. The simulation model of transmission line
图3. 输电线路仿真模型
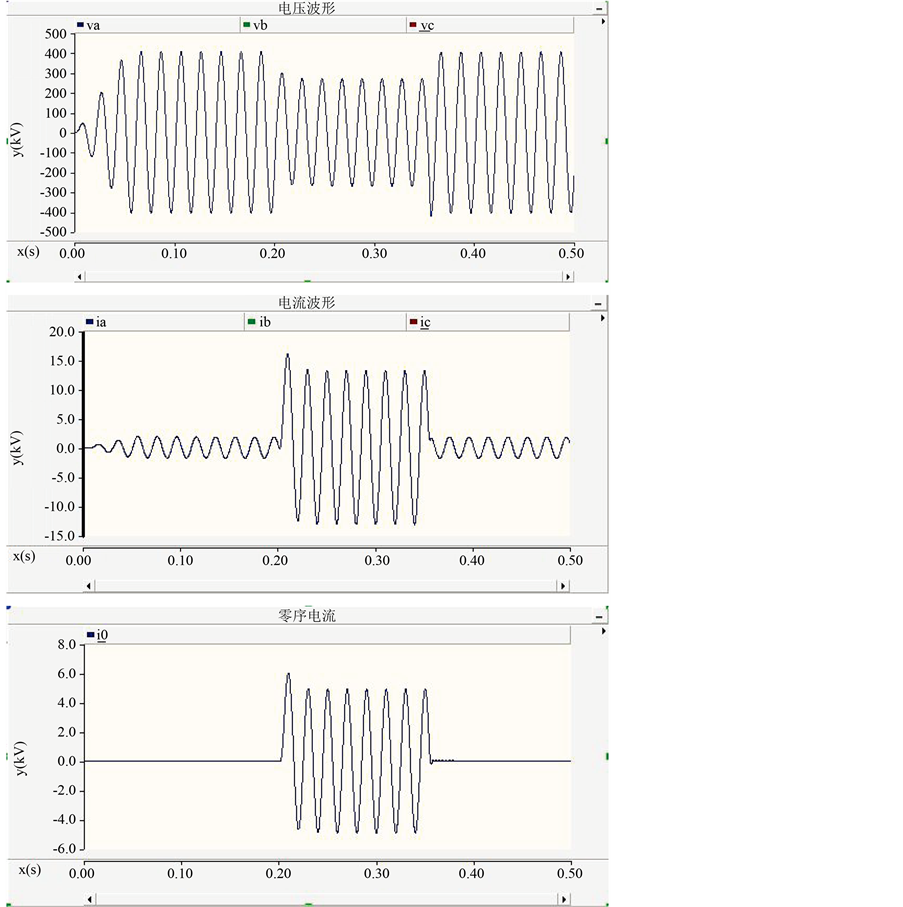
Figure 4. The A phase voltage waveform, the A phase current waveform, the zero sequence current waveform
图4. A相电压波形、A相电流波形、零序电流波形
Table 1. The results of fault location
表1. 故障测距结果
Table 2. Influence of sampling period on measurement accuracy
表2. 采样周期对测距精度的影响
4. 实例分析
4.1. 线路信息介绍
借助录波装置V10256X在福建霞浦小沙110 kV大京风电线发生故障时所采集的数据对故障点进行测距,线路全长27.3 km,故障距离9 km,导线型号LGJ-240,单位长度正序阻抗z1 = 0.22 + 0.8i,单位长度零序阻抗z0 = 0.66 + 2.3i,录波起始时间2011年6月10日10时37分20秒723毫秒,线路于10时37分20秒934毫秒发生C相短路接地故障,断路器动作时刻10时37分21秒612毫秒。
4.2. 采样周期选取
利用Matlab对录波器采集到的故障信息进行提取,绘制零序电压波形,见图5、图6、图7。
通过以上三个图可以看出,自故障发生后到故障切除这段期间,母线零序电压的波形并不是一直处于稳定的状态,故障发生时波形起伏较大,而故障切除前的电压波形相较于其他时刻最为稳定。故障发生时线路电流波形具有同样特点,见图8。
4.3. 故障测距
以断路器动作前一个周期的采样数据进行测距为例,录波器采样频率为3200 Hz,一个采样周期有3200/50 = 64个采样点,利用Matlab将傅立叶算法编程,求得母线电压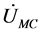 为83.2596 + 33.3356i,故障相电流
为83.2596 + 33.3356i,故障相电流 为0.6445 + 0.1419i,零序电流
为0.6445 + 0.1419i,零序电流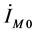 为0.5656 + 0.1377i,零序补偿系数K = 0.6279 − 0.01.0i,将求得的数据代入式(1-6),为消去
为0.5656 + 0.1377i,零序补偿系数K = 0.6279 − 0.01.0i,将求得的数据代入式(1-6),为消去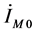 ,两边同乘
,两边同乘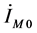 的共轭,因结果为复数,对左右两边同时取虚部如式(1-7),测得故障距离为9.1393 km。现从故障发生时刻10时37分20秒934毫秒到断路器动作时刻10时37分21秒612毫秒,利用故障发生后第一个周期、断路器动作前一个周期及故障持续时间内任意两个周期进行测距,测距方法如前述,可得不同采样周期所得测距结果见表3。
的共轭,因结果为复数,对左右两边同时取虚部如式(1-7),测得故障距离为9.1393 km。现从故障发生时刻10时37分20秒934毫秒到断路器动作时刻10时37分21秒612毫秒,利用故障发生后第一个周期、断路器动作前一个周期及故障持续时间内任意两个周期进行测距,测距方法如前述,可得不同采样周期所得测距结果见表3。

Figure 5. Zero sequence voltage waveform
图5. 零序电压波形
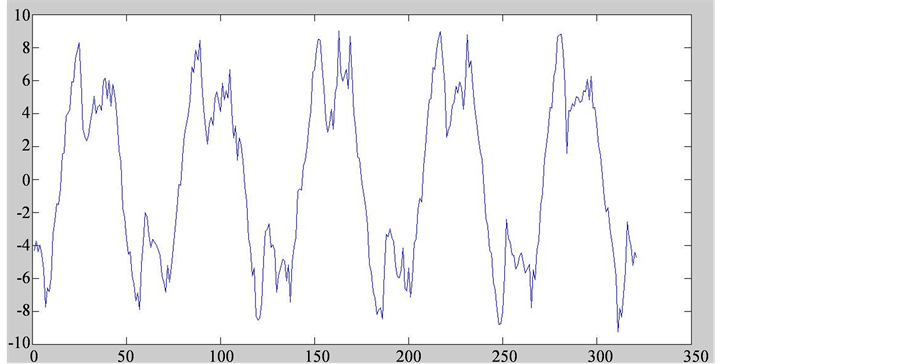
Figure 6. Five cycle zero sequence voltage waveform at any times
图6. 故障期间任意时刻五个周期母线零序电压波形

Figure 7. Five cycle zero sequence voltage waveform before Circuit breaker trip
图7. 断路器动作时前五个周期母线零序电压波形
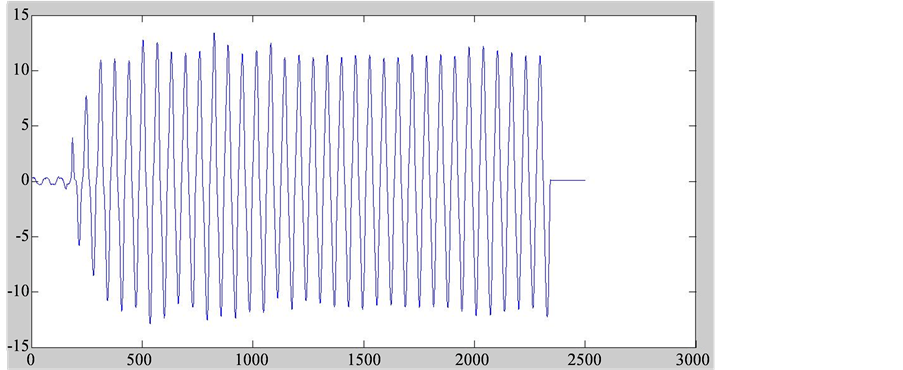
Figure 8. The C phase current waveform
图8. C相电流波形
Table 3. The results of fault location
表3. 故障测距结果
由表3可以看出基于工频分量的单端故障测距算法对采样周期的选取有较高的要求,选取不同采样周期会对测距结果产生一定影响,如果采样周期选取故障发生后波形起伏较大的时刻,会对故障点的确定有较大的影响,而断路器动作前,波形基本处于稳定状态,利用断路器动作前一个周期进行测距能满足测距精度的要求。
5. 总结
本文通过仿真建模及线路故障实例对线路发生单相接地短路故障时,选取不同采样周期对测距精度的影响进行分析。通过分析可知选取不同的采样周期会对测距结果产生较大影响,所以在采样周期的选取上应选择波形平稳的时期,如断路器动作前一个周波。对输电线路发生故障时采样周期的选取有借鉴意义,同时可以对线路发生其它类型故障时采样周期的选取提供参考。
文章引用
孟祥飞,孙懿君,郝洪民,王 建. 输电线路发生单相接地短路后采样周期对测距精度的影响
Influence of Sampling Period on the Accuracy of Single Phase to Ground Fault in Transmission Line[J]. 智能电网, 2016, 06(02): 47-55. http://dx.doi.org/10.12677/SG.2016.62006
参考文献 (References)
- 1. 贺家李, 葛耀中. 超高压输电线路故障分析与继电保护[M]. 北京: 科学出版社, 1987.
- 2. 秦华锟. 高压输电线路故障测距算法综述[J]. 电力系统自动化, 2003, 27(6): 66-69.
- 3. 李光琦. 电力系统暂态分析(第三版)[M].中国电力出版社, 2006: 3-4.
- 4. 黄少锋, 曹凯, 罗澜. 一种消除过渡电阻影响的阻抗测量方法[J]. 电力系统自动化, 2013: 108-113.
- 5. 吕艳萍. 一种消除过渡电阻对距离保护影响的新算法[J]. 电力与电工, 2009(9): 13-15.
- 6. 仲崇权, 兰敬辉, 杨素英. 一种消除分布电容影响的电阻测量方法[J]. 大连理工大学学报, 2003(5): 372-376.
- 7. 葛耀中. 新型继电保护和故障测距的原理与技术(第二版)[M]. 西安: 西安交通大学出版社, 2007: 256-257.
- 8. 胡帆, 刘沛, 程时杰. 高压输电线路故障测距算法仿真研究[J]. 中国电机工程学报, 1995, 15(1): 67-72.
