Smart Grid
Vol.08 No.02(2018), Article ID:24252,8
pages
10.12677/SG.2018.82011
A New Fault Location Method for Distribution Network Based on Bayes Likelihood Ratio
Wenjun Ren, Xiaofu Xiong
State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing

Received: Mar. 12th, 2018; accepted: Mar. 21st, 2018; published: Mar. 28th, 2018

ABSTRACT
In order to realize the fast fault-tolerant fault location of the distribution network under nonperfect fault information, a three-phase current information is put forward in the terminal opening space, and the main station is uploaded. After failure, reported by distribution network fault after the feeder switch remote communication between each phase fault alarm signal, remote measure between three phase fault current and three-phase fault current with the phase correlation between fault alarm signal, omission, false alarm for the presence of terminal equipment to report the fault alarm signal correction. A fault addressing model based on this algorithm is established, and the Bayes likelihood ratio operation is performed to locate the fault in the maximum probability of failure. The algorithm is simple and practical, which can block the errors of SCADA data to a certain extent, and verify the accuracy and validity of the algorithm by an example.
Keywords:Distribution Network, Fault Location, Correction of Distortion Information, Likelihood Ratio of Bayes
基于贝叶斯似然比形式的配电网故障定位 新方法
任文君,熊小伏
重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆

收稿日期:2018年3月12日;录用日期:2018年3月21日;发布日期:2018年3月28日

摘 要
为实现非健全故障信息下配电网的快速容错故障定位,提出在终端开辟空间储存采集的三相电流信息,并上传主站。故障后,主站利用配电网故障后各馈线开关上报的遥信量各相故障报警信号之间,遥测量三相故障电流之间以及三相故障电流与各相故障报警信号之间的相关性,对终端设备上报的存在漏报、误报的故障报警信号进行修正;建立基于该算法的故障寻址模型,根据查表判断出故障回路,进行贝叶斯似然比运算,在最大故障概率条件下进行故障定位。算法简洁、实用,能够在一定程度上屏蔽SCADA数据的错误和崎变,并通过算例验证了算法的准确性和有效性。
关键词 :配电网,故障定位,畸变信息校正,贝叶斯似然比

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
配电网故障定位作为馈线故障区域准确辨识和恢复用户供电的前提,是实现配电自动化建设的重要组成部分,对于提高配电系统供电可靠性和系统自愈性具有重要的意义 [1] [2] [3] [4] 。在配电网发生故障后,根据馈线终端单元(FTU)上报的信息及时准确地判断出故障区域是配电网自动化的关键技术之一,近年来已经取得了大量的研究成果 [5] 。
目前针对基于馈线终端单元上报故障信息进行配电网故障定位的方法主要分为两类:一类是基于健全信息的故障定位方法 [6] [7] [8] [9] ;一类是基于非健全信息的故障定位方法 [5] [10] [11] [12] [13] [14] 。基于健全信息的配电网故障定位研究成果在馈线自动化系统中发挥了积极的作用,但是由于馈线终端、配电自动化设备及通信网络的运行环境恶劣,故障报警信号容易漏报或者误报,使上述基于健全信息的故障定位方法,定位结果出现错误,因此出现了基于非健全信息的故障定位的方法和故障信息的容错技术。基于非健全信息的配电网故障定位研究成果在故障信息漏报、误报的情况下都具有一定的容错能力。
以上研究成果有效解决了配电网故障区段定位的问题,提出利用配电网故障后各馈线开关上报的各相故障报警信号之间的相关性进行容错定位 [11] ,但是,仅利用了终端上报的遥信量,没有考虑到终端还可以上报遥测量的特点。同时,目前一些直接应用概率对配电网进行故障区段定位的方法存在两点不足:1) 实际电力系统中很难给出某一故障事件精确的概率;2) 对于故障事件的可能值,难以满足其和为1的规范约束。
针对上述问题,本文提出故障后综合考虑终端FTU采集的遥信量和遥信量,利用遥信量各相故障报警信号之间,遥测量三相故障电流之间以及三相故障电流与各相故障报警信号之间的相关性,实现故障报警信号的校正;建立基于该算法的故障寻址模型,将校正后的馈线开关的故障信息序列通过查表方式判断出故障回路;然后采用贝叶斯似然比进行运算,克服故障事件精确的概率难以获取的问题;在最大故障概率条件下进行故障定位,实现基于贝叶斯似然比形式的配电网故障定位新方法。
2. 配电网区段定位算实现
2.1. 贝叶斯似然比定义
首先,进行贝叶斯似然比定义介绍。若有证据A,则假设B成立,用 表示。换成概率的说法,即A发生时,B发生,且存在一定的概率,这个概率就是条件概率 。设B成立的先验概率为 ,则有贝叶斯公式:
(1)
设B1,B2分别为两个命题,由式(1)有:
(2)
式(2)称为似然比公式,它表明了后验概率比、先验概率比和样本提供的似然比之间的关系。
设事件集合 为有限集合,如前所述,要得到W上每个元素的概率值是很困难的,但是给出其似然比 相对来讲是容易的,即可以方便给出事件 比 发生的可能性更大、更小、还是相等,并且不受到 约束。
2.2. 电网畸变故障报警信号的校正
我国配电网通常为小电流接地系统,由于馈线自动化系统故障区段定位不适用于单相接地故障,所提出的故障报警信号校正的方法针对两相短路、两相接地和三相接地故障的情况。本方法仅需在终端检测处安装配置三相电流互感器,以充分利用各相信息的相关性。
同一馈线终端单元FTU上传的三相电流信息和故障报警信号同时畸变可能性极其小,而且配电网发生两相短路、两相接地、三相接地故障后,至少两相会出现故障电流,所以可利用线终端单元FTU上传的各相电流信息和各相故障报警信号之间的相关性,对终端设备单元FTU上报的存在漏报、误报的故障报警信号进行修正。
若配电网某一馈线发生故障,主站分相收集馈线终端单元FTU上报的故障报警信号,其中,fX = 1 表示某一开关的X相上报故障报警信号;fX = 0表示某一开关的X相未上报故障报警信号。同时,馈线终端单元FTU遥测上传三相故障电流信息,用IX表示某开关的X相电流,主站将搜集的三相电流与系统电流整定值比较,定义gX:
利用馈线终端单元FTU上传的各相故障报警信号之间,三相故障电流之间以及三相故障电流与各相故障报警信号之间的相关性,修正漏报或者误报故障报警信号的方法步骤如下:
1) 配电网馈线发生故障后,主站同时收集各馈线开关a、b、c三相的故障报警信号和遥测上传的三相电流信息。
2) 若主站定义的某一开关的X相的故障报警信号fX = 1,Y相的故障报警信号fY = 1,即该开关至少有两相故障报警信号为1,则判断该开关故障报警信号未发生畸变,其故障信息标志为f = 1,转至步骤5);若主站定义的某一开关的三相故障报警信号均为0,则判断该开关故障报警信号未发生畸变,故障信息标志为f = 0,转至步骤5);若主站定义某一开关的X相故障报警信号fX = 1,Y相和Z相的故障报警信号fY = 0、fZ = 0,即仅有一相的故障报警信号为1,则判断出该开关的故障报警信号发生畸变,需要对该开关畸变的报警信号进行误报或者漏报检验。
3) 将主站收集的该开关a、b、c三相的电流信息与整定值比较,同样定义,若该开关任一相电流大于系统电流整定值,则定义gX = 1;反之,则定义gX = 0:
a) 若存在故障报警信息畸变的开关fX = gX = gY = 1,fY = 0,则判断该开关Y相故障报警信号为漏报;
b) 若存在故障报警信息畸变的开关fY = gX = gY = 0,fX = 1,则判断该开关X相故障报警信号为误报。
4) 根据故障报警信号误报、漏报的检验结果,对存在误报或者漏报的故障报警信号进行修正,给出健全的故障信息。
a) 若该开关Y相存在故障报警信号漏报,则将该开关Y相故障报警信号修正为1,即fY = 1,最后得到该开关故障信息标志为f = 1;
b) 若该开关X相存在故障报警信息误报,将该开关X相故障报警信号修改为0,即fX = 0,最后得到该开关故障信息标志为f = 0。
5) 根据修正后的各开关的故障信息标志f,最终得到故障信号序列
2.3. 配电网的故障区段定位
2.3.1. 配电网络拓扑结构定义
如图1所示,将馈线区域与该区域源点开关对应统一编号的方法进行编号,其中: 为负荷开关; 为支路编号,并且做如下定义:
1) 支路末端:除独立电源外,只和一个开关关联的支路如图1中的 。
2) 回路:从电源节点沿馈线向线路末端供电所经历的馈线开关的有序集合。如 构成一个回路。
3) 回路故障信号序列:SCADA系统接收到在回路各馈线开关上安装的检测装置上测得的故障信息,根据上传的故障指示信号形成有序集合 ,其中fi为按照上小节步骤校正后的值,1表示有故障信号,0表示无故障信号。
2.3.2. 故障回路判断
从主站出线口开始,自上而下,根据负荷开关对上述配电网进行结构分层,并且生成相应的回路,如表1所示。由上述定义可知,上传的故障指示信号形成有序集合
中的
是与馈线开关
对应的,则可以根据
的状态,通过查表方式从底层第5层向上逐层历遍,根据
的状态去判断故障发生对应的回路。例如,
序列中若出现
,其对应的负荷开关为N9,则查表1,可判断故障发生在
故障回路,对应回路故障信号序列 。
。
2.3.3. 故障概率似然比判别
由于实际配电网在一条馈线上同时出现2处及以上故障支路的概率很小,几乎可以忽略不计,据此假设如下:
1) 在SCADA系统中,每个开关上FTU报警的错误和向上通信时出错的概率是均等的,定义为p且 。
2) 同一条馈线上同时发生2处及以上故障的概率为0,SCADA,系统接收到故障信息时,故障点必在该故障信息指示的回路上。
3) 配电网中任何一条支路发生故障的概率都相同。
在上一小节判断出回路故障信号序列后,利用贝叶斯公式的似然比进行故障定位的模型。假设

Figure 1. The network diagram of distribution system
图1. 配电网络图
Table 1. Distribution network stratification
表1. 配电网分层划分
SCADA系统接收到故障回路中负荷开关 传来的故障信号序列 ,半段支路 发生故障的概率用 ,根据条件概率的贝叶斯公式:
(3)
若直接计算 ,需要知道 、 和 ,但在实际中要得到 和 是比较困难的,而且也没有必要,只需要判断支路 比支路 发生故障的可能性更大、更小还是相等。因此,将似然比的形式引入故障定位中,定义故障概率的似然比为 :
(4)
根据上述假设可知, ,所以,
(5)
其中 为支路 发生故障,且 所在回路上的FTU检测并上报到SCADA系统的故障信号序列为F概率。
在上述假设的基础上计算 :
(6)
式中 是检测到的非故障信号, 是检测到的故障信号。
由式(5)可以得到 ,根据 就可以知道支路 与支路 发生故障的可能性比较:
1) ,支路 比 发生故障的可能性大;
2) ,支路 与 发生故障的可能性相等;
3) ,支路 比 发生故障的可能性小。
上述定义可以推广到具有n条支路的情况,对n条支路进行故障似然比运算,结果如下:
(7)
出现故障概率最大的认为必是发生故障的区段,则负荷开关 对应的支路必是故障支路。
2.4. 算法实现流程
本文算法主要的计算步骤如图2所示。

Figure 2. Flow chart of fault location algorithm in distribution network
图2. 配电网故障定位算法流程图
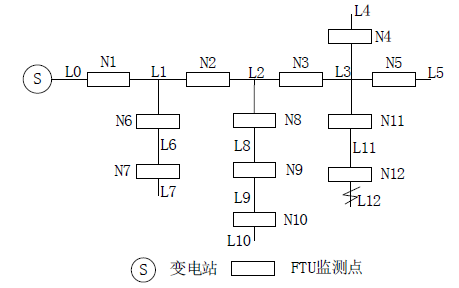
Figure 3. Distribution network with lasting fault occur to L12
图3. L12发生永久故障的配电网络
3. 算例分析
如图3所示,假设在支路 发生了永久性的a-b相间故障后,上级SCADA系统接收到配电网所有负荷开关的故障信号为 , , , , , , , , , ,其余负荷开关a、b两相故障信号都为零;其中1代表有故障信号,0代表无故障信号。
认真对比分析可知, 开关自身a、b两相故障信息存在矛盾。此时,此时需要主站再次根据馈线终端 上传a、b两相的电流信息 , 与整定值 比较,得出过流信息。经判断可知 , ;所以 开关的b相存在漏报,将 更新校正为1,即故障信号序列 。根据 中每个元素对应 的状态,在表1中从第5层开始逐层向上查表,可以发现第5层中 ,则可判断 为故障回路,对应的回路故障信号序列为 ,根据式(6)、(7)可知:
(8)
将式(8)中的各项代入(5)式进行似然比计算比较大小,以 、 比较为例,
(9)
由于 ,所以 ,支路 比 发生故障的可能性大;同理,对其项依次判断,最后可以得出 概率最大;所以支路 发生故障,与实际相吻合。
如果这时由于信号传输或其他原因,导致信号指示无法正常校正,假设系统中的 指示出现错误,使上传到SCADA的故障信息为 ,此时如果采用故障位置判断原则“当支路的两端开关中,一个流过短路电流,另一个未流过短路电流,则该支路故障”就会出错,认为支路 和支路 都是故障点。而采用式(6)、(7)可知:
(10)
将式(10)中的各项代入(5)式进行似然比计算比较大小,以 、 比较为例,
(11)
由于 ,所以 ,支路 比 发生故障的可能性大;同理,对其项依次判断,最后可以得出 概率最大;同样可以判断出支路 发生故障,也与实际相吻合。由此可知,即使在馈线开关指示错误造成SCADA检测到故障信号序列出现畸变且无法用上述方法进行校正时,运用这种方法仍能够准确地进行故障定位,具备良好的容错性。
4. 结论
本文结合配电网实际情况,提出了基于贝叶斯公式的似然比形式的故障定位算法。该算法以SCADA信息为判断依据,综合考虑终端FTU采集的遥信量和遥信量,实现故障报警信号的校正;建立基于该算法的故障寻址模型,根据查表判断出故障回路;然后采用似然比进行运算,克服了故障事件精确的概率难以获取的问题;在最大故障概率条件下进行故障定位,最终实现配电网故障定位新方法。算法简洁、实用,能够在一定程度上屏蔽SCADA数据的错误和崎变,并通过算例验证了算法的准确性和有效性。
文章引用
任文君,熊小伏. 基于贝叶斯似然比形式的配电网故障定位新方法
A New Fault Location Method for Distribution Network Based on Bayes Likelihood Ratio[J]. 智能电网, 2018, 08(02): 97-104. https://doi.org/10.12677/SG.2018.82011
参考文献
- 1. 郭壮志, 徐其兴, 洪俊杰, 等. 配电网快速高容错性故障定位的线性整数规划方法[J]. 中国电机工程学报, 2016, 36: 1-9.
- 2. 牛耕, 周龙, 裴玮, 等. 基于克拉克电流相角差值的低压有源配电网故障定位方法[J]. 中国电机工程学报, 2015, 35(S): 15-24.
- 3. 张姝, 杨健维, 何正友, 等. 基于线路暂态重心频率的配电网故障区段定位[J]. 中国电机工程学报, 2015, 35(10): 2463-2470.
- 4. 倪广魁, 鲍海, 张利, 等. 基于零序电流突变量的配电网单相故障带电定位判据[J]. 中国电机工程学报, 2010, 30(31): 118-122.
- 5. 刘健, 赵倩, 程红丽, 等. 配电网非健全信息故障诊断及故障处理[J]. 电力系统自动化, 2010, 34(7): 50-56.
- 6. 刘健, 贠保记, 崔琪, 等. 一种快速自愈的分布智能馈线自动化系统[J]. 电力系统自动化, 2010, 34(10): 82-86.
- 7. 刘健, 赵树仁, 贠保记, 等. 分布智能型馈线自动化系统快速自愈技术及可靠性保障措施[J]. 电力系统自动化, 2011, 35(17): 67-71.
- 8. 焦振有, 焦邵华, 刘万顺. 配电网馈线系统保护原理及分析[J]. 电网技术, 2002, 26(12): 75-78.
- 9. 章琦. 基于面保护原理的配电网故障处理[J]. 浙江电力, 2002, 21(2): 14-17.
- 10. 刘文轩, 严凤, 田霖, 等. 基于LVQ 神经网络的配电网故障定位方法[J]. 电力系统保护与控制, 2012, 40(5): 90-95.
- 11. 刘健, 董新洲, 陈星莺, 等. 配电网容错故障处理关键技术研究[J]. 电网技术, 2012, 36(1): 253-257.
- 12. 郭壮志, 吴杰康. 配电网故障区间定位的仿电磁学算法[J]. 中国电机工程学报, 2010, 30(13): 34-40.
- 13. 王英英, 罗毅, 涂光瑜. 基于贝叶斯公式的似然比形式的配电网故障定位方法[J]. 电力系统自动化, 2005, 29(19): 54-57.
- 14. 郑涛, 潘美玉, 王英男, 等. 配电网具有容错性的快速故障定位方法研究[J]. 电力系统保护与控制, 2014, 42(6): 63-67.
