计及多小水电接入配电线路的线损计算方法及降损措施研究 Losses Calculation Method and Reduction Measures of Distribution Line with Multi-Small Hydropower

doi:10.12677/SG.2020.101001

Smart Grid
Vol. 10 No. 01 ( 2020 ), Article ID: 33834 , 10 pages
10.12677/SG.2020.101001

Losses Calculation Method and Reduction Measures of Distribution Line with Multi-Small Hydropower

Yi Li¹, Hongzhou Chen², Ming Huang¹, Xiaoping He¹, Zheng Ma², Xingtian Chen³

●How to Cite this Article

¹State Grid Chongqing Electric Power Co., Wulong Power Supply Branch Company, Chongqing

²State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing

³Chongqing Yuanhu Technology Co. Ltd., Chongqing

Received: Dec. 13^th, 2019; accepted: Dec. 30^th, 2019; published: Jan. 6^th, 2020

ABSTRACT

Line loss is an important index to evaluate the rationality of distribution network planning and operation. With multi-small hydropower units being connected to the distribution network successively, the bidirectional flow characteristics of power flow in the distribution network become increasingly prominent, which increases the difficulty of line loss calculation. In this paper, a line loss calculation model for distribution lines including multi-small hydropower is established, and the analytical formula for line loss of each segment is derived by means of root mean square current method, and the related loss reduction measures are proposed. Combined with specific examples, the line loss values of distribution network in different scenarios are compared, and the effectiveness of loss reduction measures is verified.

Keywords:Distribution Network, Small Hydropower, Line Loss, Sensitivity

计及多小水电接入配电线路的线损计算方法及降损措施研究

李毅¹，陈红州²，黄明¹，何小平¹，马政²，陈星田³

¹国网重庆市电力公司武隆供电分公司，重庆

²输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆

³重庆元虎科技有限公司，重庆

收稿日期：2019年12月13日；录用日期：2019年12月30日；发布日期：2020年1月6日

摘要

线损是评价配电网规划和运行合理性的一项重要指标，对于供电部门开展日常管理工作至关重要。随着众多小水电机组陆续接入配电网，配电网潮流的双向流动特征逐渐突出，增加了线损计算的难度。本文建立了计及小水电多点接入的配电线路线损计算模型，应用均方根电流法推导了各段线路的线损解析公式，并据此提出了相关降损措施。结合具体算例，对比了不同场景下配电网的线损值，验证了所提降损措施的有效性。

关键词 :配电网，小水电，线损，灵敏度

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

小水电属于分布式发电，通常是指装机容量低于50 MW的水电站 [1]。其一般属于径流式，出力会随着水流量的大小而变化，表现出较明显的季节变化特性 [2] [3]。近年来，小水电作为一种清洁能源，以其运行方式灵活、开发技术成熟、投资成本较低的优点得到了良好的发展。我国水资源分布广泛，但大型水电站往往不便于为偏远山区远距离送电 [4] [5]。通过小水电开发，可以充分利用这些偏远地区的丰富水资源，在提高其河流的治理能力的同时，也能有效解决用户用电困难的问题。所以，小水电开发可以推动偏远山区的电气化进程，也是协调生态环境发展的重要举措 [5] [6] [7]。

小水电开发在带动经济发展的同时，也为配电网的日常运行带来了影响。由于小水电容量有限，输出功率会随着环境的影响表现出较大的波动性，一般根据出力随季节的变化特征，把一年分为丰水期和枯水期 [8] [9]。夏季降水较多，小水电出力一般为满发状态；而冬季降水一般较少，小水电仅能达到部分出力。传统的辐射状配电网潮流是从变电站流向负荷节点，而加入小水电后也增加了配电网功率流向的复杂性。丰水期的小水电出力，除了能满足负荷之外，甚至会向电网倒送功率，导致线损增大 [10] [11] [12]。因此，研究小水电接入配电网后的影响十分重要。

文献 [13] 对比均方根电流法与改进等效容量法的优缺点，最终采用均方根电流法计算了丰顺电网中多水电出力配电线路的线损；文献 [14] 将小水电视作容量为负的变压器进行统计计算，并采用等值电阻法计算了10 kV线路的理论线损；文献 [15] 对配电变压器、低压配电线路、接户线和电度表等的电能损耗进行了分析，并提出采用均方根电流法来计算低压线损；文献 [16] 考虑了分布式电源多点随机注入配电网的特点，建立了准确高效的分布式电源模型；文献 [17] 基于平均电流法及其误差，考虑分布式电源已知运行参数，提出了一种改进的含分布式电源的配电网理论线损计算方法。但以上文献均没有推导计及多小水电出力时的配电线路理论线损公式，如何具体结合影响线损的因素提出降损措施还有待研究。

据此，本文首先介绍了几种传统计算线损的理论方法，然后建立考虑小水电出力的配电线路模型，推导理论线损公式以及每台小水电对线损的贡献。最后，结合算例对比分析小水电在不同场景下的线损值，并对具体降损措施的可行性进行验证。

2. 线损计算方法

目前已有的理论线损研究计算方法总体上可分为三大类型：第一类为以均方根电流法、等值电阻法、最大电流法、平均电流法及电压损失法为代表的传统线损计算方法；第二类为基于潮流算法的牛顿拉夫逊法以及前推回代法；第三类为基于特征参数进行数学建模的线损计算方法，如多元回归法，人工智能算法等等 [18] [19] [20]。

2.1. 均方根电流法

假设某三相元件流过的电流为 $I (t)$ ，测计时段为T，则其均方根电流 $I_{rms}$ 为

$I_{rms} = \sqrt{\int_{0}^{T} I^{2} (t) d t / T}$ (1)

若该元件的电阻为R，则三相元件的电能损耗 $Δ A (kW \cdot h)$ 为

$Δ A = 3 R \int_{0}^{T} I^{2} (t) d t \times 10^{- 3}$ (2)

若实测的是三相有功功率、无功功率和线电压时，则有

$3 I_{rms}^{2} = \frac{1}{T} \sum_{0}^{T} \frac{P^{2} + Q^{2}}{U^{2}}$ (3)

$I_{rms} = \sqrt{\frac{\sum_{0}^{T} \frac{P^{2} + Q^{2}}{U^{2}}}{3 T}}$ (4)

式中： $P_{t}$ 、 $Q_{t}$ 为代表日正点时通过该元件电阻的三相有功功率和无功功率； $U_{t}$ 为与 $P_{t}$ 、 $Q_{t}$ 同一测量端同一时间的线电压。

均方根电流法可以应用于进行含多小水电的配电线路理论线损计算。其主要思路是将使用绝对值计算出来的小水电均方根电流加负号，目的是区别于各配变负荷均方根电流为正；然后再使用叠加原理计算配电线路各段线路的均方根电流值，利用各段线路均方根电流值计算各段线路损耗；最后使各段线路损耗相加，再加上配变损耗即可求得配电线路线损。

2.2. 等值电阻法

等值电阻法是基于均方根电流法衍生出的线损计算方法。为了弥补在精度上的不足，其基本思路是通过构建一个虚拟的等值电阻来模拟配电网线路电阻和变压器电阻，以避免收集大量的电网数据。

$Δ P = 3 \sum_{i = 1}^{n} I_{i}^{2} R_{i} = 3 I^{2} R_{e l}$ (5)

其中， $R_{i}$ 为第i段线路的电阻， $I_{i}$ 为第i段线路的电流，n为该馈线的总段数。

根据等值电阻原理，电能损耗可以利用电阻线路出口的电流或总功率的叠加来进行换算，提高了计算的方便性和可操作性。

2.3. 最大电流法

最大电流法根据均方根电流与最大电流的等效关系进行计算，由于计算出来的线损较大，所以需要乘以一个小于1的修正系数F，即损失系数。

$F = \frac{I_{rms}^{2}}{I_{\max}^{2}}$ (6)

其中， $I_{\max}$ 为最大负荷电流。

2.4. 平均电流法

平均电流法也称为形状系统法，与最大电流法类似，利用均方根电流与平均电流的等效关系进行计算，由于计算出来的线损较小，所以需要乘以一个大于1的修正系数F，即形状系数。

$K^{2} = \frac{I_{rms}^{2}}{I_{a r}^{2}} = \frac{α + \frac{1}{3} {(1 - α)}^{2}}{{(\frac{1 + α}{2})}^{2}}$ (7)

其中， $I_{a r}$ 为平均电流， $α$ 为最小负荷率。

3. 考虑小水电的线损简化计算模型

假设所有小水电集中为一个小水电，所有负荷集中在配电线路时如图1所示，分析配电线路上的损耗。

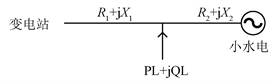
Figure 1. Simplified schematic diagram of a small hydropower network

图1. 含有小水电的配电线路简化图

3.1. 小水电不参与发电

当小水电不参与发电时，配电线路的损耗为：

$Δ P = \frac{S_{L}^{2}}{U_{N}^{2}} R_{1}$ (8)

式中， $Δ P$ 为配电线路的总线损， $S_{L}$ 为负荷的视在功率， $R_{1}$ 为线路的电阻。即此时配电线路中小水电不会引起多余的损耗，仅存在由负荷引起的线路损耗。

3.2. 小水电参与发电

当小水电参与发电时，配电线路的损耗为：

$Δ P^{'} = Δ P_{1} + Δ P_{2} = \frac{{(S_{L} - S_{水电})}^{2}}{U_{N}^{2}} R_{1} + \frac{S_{水电}^{2}}{U_{N}^{2}} R_{2}$ (9)

通过作差，得到

$Δ P_{a d d} = Δ P^{'} - Δ P = \frac{S_{水电} [S_{水电} (R_{1} + R_{2}) - 2 S_{L} R_{1}]}{U_{N}^{2}}$ (10)

则当，即 $Δ P_{a d d} > 0$ 时，其线路损耗反而比小水电不参与发电时大；反之，其比小水电不发电时小。因此有

$\frac{S_{水电}}{S_{L}} > \frac{2 R_{1}}{(R_{1} + R_{2})}$ (11)

特殊的，若 $S_{水电} > 2 S_{L}$ ，线路损耗都会变大。

通过上式可以初步通过小水电容量与线路参数之间的关系判断配电线路总线损的大小，但在实际中，每台小水电对线损的贡献度有差别。为分析出线损与每台小水电出力之间的关系，假设配电网中某条馈线如图2所示，该馈线上共有n个节点，其中有若干个负荷节点和小水电。

Figure 2. Distribution line diagram with n nodes

图2. n节点配电线路示意图

则该配电线路上的线损为

$Δ P = Δ P_{R - L} + Δ P_{R - S D}$ (12)

其中， $Δ P$ 为配电线路总线损， $Δ P_{R - L}$ 为节点之间的线损， $Δ P_{R - S D}$ 为小水电电源与配电线路之间的线损。

3.2.1. 节点之间的线损

将线路划分为n段，则整条线路的线损为：

$Δ P_{R - L} = Δ P_{0, 1} + Δ P_{1, 2} + \dots + Δ P_{m, m + 1} + \dots + Δ P_{r, r + 1} + \dots + Δ P_{n - 1, n}$ (13)

节点n − 1与节点n之间的线损为：

$Δ P_{n - 1, n} = \frac{{[{(- 1)}^{x_{n}} S_{n}]}^{2}}{U_{N}^{2}} R_{n - 1, n}$ (14)

同理，节点n − 2与节点n − 1之间的线损为：

$Δ P_{n - 2, n - 1} = \frac{{[{(- 1)}^{x_{n - 1}} S_{n - 1} + {(- 1)}^{x_{n}} S_{n}]}^{2}}{U_{N}^{2}} R_{n - 2, n - 1}$ (15)

以此类推，节点0与节点1之间的线损为：

$Δ P_{0, 1} = \frac{{[{(- 1)}^{x_{1}} S_{1} + {(- 1)}^{x_{2}} S_{2} + \dots + {(- 1)}^{x_{n - 1}} S_{n - 1} + {(- 1)}^{x_{n}} S_{n}]}^{2}}{U_{N}^{2}} R_{0, 1}$ (16)

其中， $U_{N}$ 为配电线路的基准电压， $R_{n - 1, n}$ 为节点n − 1与节点n之间线路的阻抗， $Δ P_{n - 1, n}$ 为节点n − 1与节点n之间的线损， $x_{n}$ 为节点n所连接是否为小水电的判断依据，1为小水电、0为负荷。

3.2.2. 小水电电源与配电线路之间的线损

$Δ P_{R - S D} = Δ P_{1} + Δ P_{2} + \dots + Δ P_{r} + \dots + Δ P_{n}$ (17)

易知， $Δ P_{n} = x_{n} \frac{S_{n}^{2}}{U_{N}^{2}} R_{n}$ ，则

$Δ P_{R - S D} = \sum_{i = 1}^{n} x_{n} \frac{S_{n}^{2}}{U_{N}^{2}} R_{n}$ (18)

其中， $R_{n}$ 为节点n与该节点所连接的小水电之间线路的阻抗， $Δ P_{n}$ 为节点n与该节点所连接的小水电之间的线损。

3.2.3. 某台小水电对配电线路总线损的贡献

假设节点n上接了一台小水电，则该台小水电对节点n − 1与节点n之间的线损的灵敏度为

$\frac{\partial Δ P_{n - 1, n}}{\partial S_{n}} = {(- 1)}^{x_{n}} \frac{2}{U_{N}^{2}} [{(- 1)}^{x_{1}} S_{1} + {(- 1)}^{x_{2}} S_{2} + \dots + {(- 1)}^{x_{n - 1}} S_{n - 1} + {(- 1)}^{x_{n}} S_{n}] R_{0, 1}$ (19)

则该台小水电对配电线路节点之间线损的贡献为

$\frac{\partial Δ P_{R - L}}{\partial S_{n}} = \frac{\partial Δ P_{0, 1}}{\partial S_{n}} + \frac{\partial Δ P_{1, 2}}{\partial S_{n}} + \dots + \frac{\partial Δ P_{n - 1, n}}{\partial S_{n}}$ (20)

$\frac{\partial Δ P_{R - L}}{\partial S_{n}} = {(- 1)}^{x_{n}} \frac{2}{U_{N}^{2}} {[\sum_{i = 1}^{n} {(- 1)}^{x_{n}} S_{n}] R_{0, 1} + [\sum_{i = 2}^{n} {(- 1)}^{x_{n}} S_{n}] R_{1, 2} + \dots + [{(- 1)}^{x_{n}} S_{n}] R_{n - 1, n}}$ (21)

$\frac{\partial Δ P_{R - L}}{\partial S_{n}} = {(- 1)}^{x_{n}} \frac{2}{U_{N}^{2}} {{(- 1)}^{x_{1}} R_{0, 1} S_{1} + {(- 1)}^{x_{2}} (R_{0, 1} + R_{1, 2}) S_{2} + \dots + {(- 1)}^{x_{n}} (\sum_{i = 1}^{n} R_{n - 1, n}) S_{n}}$ (22)

此外，该台小水电对小水电与配电线路之间线损的灵敏度为

$\frac{\partial Δ P_{R - S D}}{\partial S_{n}} = \sum_{i = 1}^{n} 2 x_{n} \frac{S_{n}}{U_{N}^{2}} R_{n}$ (23)

则可以得到，该台小水电对配电线路总线损的贡献为

$\frac{\partial Δ P}{\partial S_{n}} = \frac{\partial Δ P_{R - L}}{\partial S_{n}} + \frac{\partial Δ P_{R - S D}}{\partial S_{n}}$ (24)

通过计算出每台小水电对配电线路总线损的贡献，可以计算出每台小水电在不同工况时对配电线路总线损的影响占比，从而可以根据占比来收取小水电的过网费，保障运行过程中的经济性。

4. 降损措施

根据线损的理论计算公式和每台小水电对配电线路总线损的贡献，可以对比观察得到对线损贡献较大的小水电，从而针对性的改变线路电阻和小水电出力以达到降低线损的目的。

4.1. 优化配电线路区段导线截面

由式(13)得，每一段线损与导线电阻成正比。在输送负荷不变的情况下，通过减小线路电阻的思路来降低线损。可以通过直接法，即增大导线截面、增加并列线路运行等措施来减小线路电阻，也可以通过改造线路布局来减小电源和负荷的距离，从而可以达到降损节电的效果。

特别地，由式(13)~(15)得

$\frac{\partial Δ P_{n - 1, n}}{\partial R_{n - 1, n}} = \frac{{[{(- 1)}^{x_{n}} S_{n}]}^{2}}{U_{N}^{2}}$ (25)

$\frac{\partial Δ P_{n - 2, n - 1}}{\partial R_{n - 2, n - 1}} = \frac{{[{(- 1)}^{x_{n - 1}} S_{n - 1} + {(- 1)}^{x_{n}} S_{n}]}^{2}}{U_{N}^{2}}$ (26)

$\frac{\partial Δ P_{0, 1}}{\partial R_{0, 1}} = \frac{{[{(- 1)}^{x_{1}} S_{1} + {(- 1)}^{x_{2}} S_{2} + \dots + {(- 1)}^{x_{n - 1}} S_{n - 1} + {(- 1)}^{x_{n}} S_{n}]}^{2}}{U_{N}^{2}}$ (27)

负荷和水电出力一定时，通过对比每段线路的电阻对线损的贡献，筛选出对线损贡献较大的导线位置，则可以优先选择所需要更换导线的位置。

假设节点s到节点s + 1之间线路电阻为R，长度为L，线损为 $Δ P_{s, s + 1}$ ，更换单位长度的线路需要投资x元，则更换后整段线路电阻变为 $k R$ ( $0 < k < 1$ )，线损为 $k Δ P_{s, s + 1}$ 。假设在电价为f的运行时间Y内，其配电线路的单位投资效益(即投资更换单位长度导线后带来的收益)为

$C = \frac{(1 - k) Y f Δ P_{s, s + 1}}{x L}$ 。 (28)

4.2. 优化小水电接入位置

由于供电区域缺少电源布点，小水电所接入的位置完全由上级电源点母线直接出线。目前，实际运行的大多数水电站距负荷中心较远，配网线路普遍较长，供电质量较低。因此，小水电接入配电网中的位置应该选取在靠近负荷的位置，使负荷能够就近消纳小水电发出的电能，避免不合理的布线增大因电能传输带来的线路损耗，尽可能实现小水电出力的本地最大利用。

特别地，如果小水电的出力较大，可以考虑设置专线输送，通过新建上级变电站，增加配电变压器的方式以达到增加电源点和缩短供电半径。

5. 算例分析

为具体分析小水电并入配电线路后对线损的影响，本文采用20节点的配电网馈线系统进行计算。其中，2、4、7、8、11、14、15、18节点为小水电(小水电满发时的出力均为400 kW)，其余为负荷节点，假设所有线路的型号均为LGJ-70 (单位电阻为0.4018 Ω/km)，具体数据见表1。应用均方根电流法，通过改变小水电的出力和改变负荷的大小来对比该配电线路的总线损。

5.1. 枯水期与丰水期总线损计算

枯水期时，小水电部分出力，将其出力设置为满发时的25%，即100 kW，可以计算出配电馈线的总线损。丰水期时，小水电满发即400 kW，可以计算出配电馈线的总线损。

图3和图4均显示配电线路的总线损随着负荷的增大先减小后增大。枯水期，即小水电出力均为100 kW，负荷为0时，配电线路的总线损为0.0276 kW。负荷增大，总线损降低，在小水电出力之和为800 kW与负荷800 kW平衡时达到最低值0.0012 kW；负荷继续增大，配电线路的总线损持续增大。丰水期，即小水电出力均为400 kW与枯水期类似，负荷为0时，配电线路的总线损为0.442 kW，比枯水期向系统反馈的电能更多，线路中的电流更大，线损也更大。负荷增大，总线损降低，在小水电出力与负荷(3200 kW)平衡时达到最低值0.0192 kW；总线损随着负荷的继续增大而持续增加。

Table 1. Branch parameters of distribution line

表1. 配电线路支路参数

(a) 枯水期负荷变化时配电线路总线损 (b) 丰水期负荷变化时配电线路总线损

Figure 3. Total line loss of distribution line when load changes in different seasons

图3. 不同季节负荷变化时配电线路总线损

可以看出，负荷为0时，小水电出力全部向系统内反送电，配电线路的线损均由小水电出力造成。随着负荷的增大，小水电的出力直接提供给负荷，多余部分再反馈给电网，使流过馈线上的电流减小，总线损也减小；当小水电出力与配电线路负荷平衡时，总线损达到最低值。往后负荷继续增大，则系统中的电流增大，总线损增大，此时由配电线路向系统反馈电能的状态转变为系统向配电线路输送电能。

5.2. 应用降损措施

5.2.1. 增大导线截面

以配电线路全年运行在不同场景为例，即小水电出力均为400 kW (丰水期)、小水电出力均为100 kW (枯水期)时，在总负荷为2400 kW不变的基础上，计算更换线路后对配电线路降低的总线路带来的单位投资效益比。若均更换为单价为5000元/km的LGJ-120 (单位电阻为0.2373 Ω/km)，每年有8个月的丰水期、4个月的枯水期，考虑电价为0.5元/KW∙h，对比更换不同导线的单位投资效益比如下图4所示。

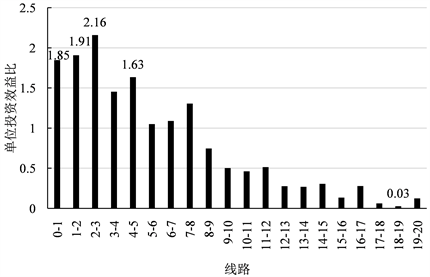
Figure 4. Efficiency ratio per unit investment after changing wire resistance

图4. 改变各段导线电阻的单位投资效益比

从图4可以看出，增大2~3段导线横截面后的单位投资效益比最大，其投资效益比为2.16，其次为1~2段、0~1段，而增大18~19段线路的横截面积对总线损的影响最小，其投资效益比为0.03。在实际工程中可以根据各段导线电阻对线损的贡献结合实际情况选择所需要改变的导线，可以保证降损过程中的经济性。

5.2.2. 更换小水电接入位置

以丰水期场景为例，即小水电出力均为400 kW时，总负荷为8000 kW，改变节点3的小水电位置。分别将节点3小水电换到节点1、5、12、15、19位置后，计算出总线损如下图5所示。

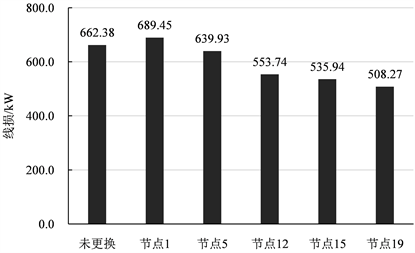
Figure 5. Comparison of line loss after changing small hydropower to different positions

图5. 改变节点3的小水电到不同位置后总线损对比

从图中可以看出，将节点3的小水电换到节点1的位置，配电线路总线损反而增加；换到其他位置总线损会有不同程度的减小。特别的，换到节点19的位置后线路的总线损为508.27 kW，其降损效果最好。在实际工程中，需要根据线路走廊可行性以及负荷中心相应确定小水电的位置，才能保证配电线路线损最低。

6. 结论

随着众多小水电逐渐接入配电网，在充分收集利用可再生能源的同时，也应研究小水电接入后配电线路的线损计算方法及降损措施。在丰水期时，小水电的出力增加，在满足本地负荷需求后，仍有较多功率反送回电网，可能远远高于平时的用电负荷，因而造成配电线路线损率增大。

本文对小水电并入配电线路后线损计算方法开展了研究，基于均方根电流法，给出了考虑不同接入点的线损计算模型，通过该模型，由小水电与线路的相关参数即可实现对配电线路总线损的计算，并进一步提出了各小水电对线损的贡献计算方法。在该模型基础上，提出了优化配电线路导线截面和优化小水电接入位置的降损方法，并通过实际算例，对两种降损措施的有效性进行了验证。由于小水电发电具有明显的季节性，在实际工程问题中需要考虑不同场景下的具体降损措施，从而保证其经济性。

文章引用

李毅,陈红州,黄明,何小平,马政,陈星田. 计及多小水电接入配电线路的线损计算方法及降损措施研究
Losses Calculation Method and Reduction Measures of Distribution Line with Multi-Small Hydropower[J]. 智能电网, 2020, 10(01): 1-10. https://doi.org/10.12677/SG.2020.101001

参考文献

1. 刘丙江. 线损管理与节约用电[M]. 北京: 中国水利水电出版社, 2005.

2. 姜富华, 杜孝忠. 我国小水电发展现状及存在的问题[J]. 中国农村水利水电, 2004(3): 82-83+86.

3. 邹体峰, 王仲珏. 我国小水电开发建设中存在的问题及对策探讨[J]. 中国农村水利水电, 2007(2): 82-84.

4. 彭智乐, 王星华, 彭显刚, 潘高峰. 基于区域同步特性的小水电出力随机建模及其准入容量评估[J]. 水电能源科学, 2015, 33(11): 171-175.

5. Elgerd, O.I. and Happ, H.H. (2007) Electric Energy Systems Theory: An Introduction. IEEE Transactions on Systems Man & Cybernetics, SMC-2, 296-297.
https://doi.org/10.1109/TSMC.1972.4309116

6. 史立山. 中国能源现状分析和可再生能源发展规划[J]. 可再生能源, 2004(5): 1-4.

7. Nadira, R., Wu, F.F., Maratukulam, D.J., Weber, E.P. and Thomas, C.L. (1990) Bulk Transmission System Loss Analysis. IEEE Transactions on Power Systems, 8, 405-416.
https://doi.org/10.1109/59.260846

8. 高久国. 探索小水电的综合管理新模式[D]: [硕士学位论文]. 杭州: 浙江大学, 2010.

9. 郑华槟. 有小水电上网线路的线损考核[J]. 农村电气化, 2005(12): 46.

10. 张海超. 基于唐山供电公司的线损分析及降损措施的研究[D]: [硕士学位论文]. 北京: 华北电力大学, 2013.

11. 黄细琴. 小水电上网对配网线损影响的解决措施[J]. 农村电气化, 2018(6): 78.

12. 陈玉波. 解决农村电网小水电并网线损增大实用方法研究[C]//云南电网公司、云南省电机工程学会. 2009年云南电力技术论坛论文集(优秀论文部分). 昆明: 云南省电机工程学会, 2009: 299-303.

13. 何伟龙. 含多小水电的配电线路降损措施研究[D]: [硕士学位论文]. 广州: 广东工业大学, 2018.

14. 谢云秋. 韶关中低压配电网线损分析及降损措施研究[D]: [硕士学位论文]. 广州: 华南理工大学, 2017.

15. 韩伟光, 宋唯, 王学庆. 均方根电流法计算低压线损[J]. 煤炭技术, 1999, 18(6): 7-8.

16. 高国梁. 分布式电源接入后的配电网降损及规划问题研究[D]: [硕士学位论文]. 济南: 山东大学, 2019.

17. 汝绪丽. 一种含分布式电源的配电网线损计算方法[D]: [硕士学位论文]. 济南: 济南大学, 2019.

18. 江木, 孙云超, 刘巨. 10 kV配电网理论线损计算方法及应用对比[J]. 供用电, 2019, 36(11): 78-83.

19. 周有学. 配电网的线损理论计算及降损措施[D]: [硕士学位论文]. 重庆: 重庆大学, 2001.

20. 樊华瑞. 多小水电接入型10 kV配电网电压控制策略研究[D]: [硕士学位论文]. 重庆: 重庆理工大学, 2018.

期刊菜单