Operations Research and Fuzziology
Vol.
09
No.
03
(
2019
), Article ID:
31597
,
7
pages
10.12677/ORF.2019.93024
A New Smoothing Newton Algorithm Based on the New Valued Function for Second-Order Cone Programming
Xiaojuan Liang
School of Mathematics and Information Science, Guangxi University, Nanning Guangxi

Received: Jul. 15th, 2019; accepted: Jul. 30th, 2019; published: Aug. 6th, 2019

ABSTRACT
Based on the Fischer-Burmeister function, a new Newton method is proposed for solving the Second-order cone programming. This algorithm adapts a new smoothing value function and proposes a Newton equation with disturbance to gain the search direction. Under suitable assumptions, we prove that the proposed new method is globally and locally quadratically convergent.
Keywords:Second-Order Cone Programming, Smoothing Newton Method, Global Convergence, Quadratical Convergence
二阶锥规划基于新价值函数的新光滑牛顿算法
梁晓娟
广西大学数学与信息科学学院,广西 南宁

收稿日期:2019年7月15日;录用日期:2019年7月30日;发布日期:2019年8月6日

摘 要
本文在Fischer-Burmeister (FB)函数的基础上,提出一种求解二阶锥规划(SOCP)问题的新光滑牛顿函数,并采用一种新的价值函数。同时用一个带扰动的牛顿方程组去获得搜索方向,在适当假设下,证明新算法具有全局收敛和局部二次收敛。
关键词 :二阶锥规划,光滑牛顿法,全局收敛,局部二次收敛

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文主要考虑以下线性二阶锥规划问题:
(1.1)
其对偶问题:
(1.2)
二阶锥规划是凸规划问题的一个重要分支,它是在仿射空间与有限个二阶锥的笛卡尔积的交集上极小化或极大化一个线性函数。在现实生活中有着广泛的应用:图论优化(文 [1] ),力学(文 [2] ),投资组合(文 [3] )等都可以转化为二阶锥规划问题求解。此外,许多数学问题也可转化为二阶锥问题求解:线性规划,二次规划,范数极小化(文 [4] ),因而研究二阶锥规划具有重要的理论与现实意义。本文在向量值FB函数的基础上进行改进得到一个新的光滑函数,并采用一个新的价值函数,给出求解二阶锥问题的一个光滑牛顿法,并证明算法是全局收敛和局部二次收敛。
2. 基础知识
为了更好地研究二阶锥规划,介绍一些与二阶锥相伴的欧几里得若当代数的基本概念以及二阶锥规划的最优性条件等。先介绍一些记号,其中U表示反射矩阵, 表示 阶单位阵, 表示一个箭形矩阵,本文用相应的大写字母表示箭形矩阵,比如 , , , 。
对于 ,定义如下若当积:
记 , 表示通常的向量的加法。
定理2.1 (谱分解定理) (文 [5] )
对向量x我们定义与二阶锥有关的谱分解为: ,其中x的谱值 和与之对应的谱向量 如下:
, 是满足 的任意向量。
定理2.2 (最优性条件) (文 [6] )如果(1.1)和(1.2)都有严格可行解,则 是(1.1)和(1.2)的最优解对当且仅当
(2.1)
对二阶锥规划,其二阶锥互补函数定义如下:
定义2.1 (文 [7] )如果向量值函数 满足
(2.2)
则称 为二阶锥互补函数。
对任意 ,定义函数 如下:
(2.3)
令
(2.4)
其中 是任意的二阶锥互补函数。易见 是与最优性条件等价的方程组,由此可知, 是 的解当且仅当 满足最优性条件,是问题(1.1)和(1.2)的最优解对。由上易知,求解此方程组的关键在于构造合适的二阶锥互补函数。由于常见的二阶锥互补函数:向量值最小函数,向量值FB函数在 点不可微(即非光滑),不能直接用牛顿法求解,为了进一步研究,先给出光滑化的概念。
定义2.2 (文 [8] )对于不可微函数 ,考虑带有参数 的函数 ,如果它具备如下性质:
(1) 对于任意的 , 是光滑的;
(2) ;
则称 是h的光滑函数。
3. 一个新的光滑函数及其性质
光滑函数在二阶锥规划算法研究中起着重要作用。由于向量值最小函数,向量值FB函数并不处处连续可微,大大影响了其实际应用。本文在FB函数的基础上通过光滑对称扰动,得到一个新的向量值函数 :
(3.1)
因此可考虑用牛顿法求解 ,但对于所构造的 ,其雅可比矩阵必须是非奇异的。在讨论 的性质之前先介绍相关结论。
引理3.1 (文 [7] )对于任意的 ,令 。则 是全局利普希茨连续的;若 ,其中 且 ,则 在 的任意邻域是连续可微的, 是强半光滑的。
引理3.2 (文 [9] )对于任意的 和 ,如果 ,则
,
且当 变为 时,上述结论仍然成立。
定理3.1设 由(2.3)式定义,令
,
则
(i) 是 上的全局利普希茨连续的处处强半光滑函数,且在 处连续可微,其雅克比矩阵为
(3.2)
其中
,
,
。
(ii) 如果矩阵A行满秩,对任意的 , 可逆。
证明:首先由引理3.1易知(i)成立。下证(ii)成立。对任意的 ,要证 可逆,只需要证方程组 只有零解,即 。将(3.2)式代入 可得
(3.3)
将 , 代入(3.3)式并将等式两端同时左乘W,得
(3.4)
因为 故由引理3.2知 与 可逆。将方程(3.4)左乘 ,由 得 。
令
,
则
(3.5)
由引理3.2知矩阵 正定,因此 ,从而 ,又矩阵A行满秩,由(3.3)式可得 ,即 只有零解,故 可逆。
4. 算法的描述
记 ,一般采用价值函数: ,本文采用价值函数: 。下面给出具体的算法描述:
算法4.1 (二阶锥规划的一个光滑牛顿法)
步骤0:(初始化)给出常数 满足 且 取 为初始点,令 ,令 。
步骤1:(终止准则)若 ,停止,否则令
,其中 , 。
步骤2:(确定搜索方向)解线性方程组 得到搜索方向 。
步骤3:(确定步长)记 是满足下式的最小非负整数l:
,
令步长 。
步骤4:(迭代更新)令 ,返回步骤1。
引理4.1令 由(2.4)式所定义,如果 ,则
(4.1)
证明:因为 ,所以 。
又因为 ,故 。又从上式第一个不等式得
,故 。综上可得(4.1)式成立。
引理4.2设 由算法的步骤2所定义,则对任意的 ,有
(4.2)
证明:对任意的 ,有 成立,故由算法的步骤2得 , ,故(4.2)式成立。
定理4.1设矩阵A行满秩,如果 ,则算法4.1是适定的。
证明:因为矩阵A行满秩且 ,由定理3.1知 可逆,所以算法4.1的步骤2是适定的。令 是步骤2中方程组的解,则对任意的 ,有
(4.3)
由于 在任意的 处连续可微,因此对任意的 ,有
(4.4)
由(4.3)式和(4.4)式得
上式第二个不等式由引理4.2可得,又因为 ,所以存在一个常数 ,使得对任意的 ,有
(4.5)
即步骤3可在有限步终止,故步骤3是适定的。综上可知,算法4.1是适定的。
5. 收敛性分析
定理5.1 (i) 设矩阵A行满秩且
是算法4.1生成的无穷迭代点列,则对
,有
,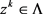 ,其中
,其中
, (5.1)
(ii) (全局收敛) 的任意聚点 都是 的解。
证明:(i) 由算法4.1的步骤4可知 单调下降,由 的定义可知 单调下降。先用数学归纳法证明 ,由算法4.1的步骤0知 ,假设 ,下证 ,由于 , ,由(4.3)式知 ,故 。
同理用数学归纳法证明 ,由算法4.1的步骤0知 ,即 ,假设 ,
下证 ,由(4.3)式可得 ,故 。
(ii) 不失一般性,设 是点列 的任意聚点,要证 ,用反证法。假设 ,由算法4.1的步骤3知 单调下降其有下界,结合 的连续性,有 。由 的定义知 单调下降且趋于 : 。另外,由(5.1)知,对任意的 ,有 ,从而 。又因为 可逆,令 为算法4.1的步骤2的解,存在一个非负整数 使得 ,当k充分大时,有 。存在 的一个闭邻域 和正数 ,使得对于任意的 和所有的 ,都有 , 非奇异且
(5.2)
由算法4.1的步骤3知,对于充分大的k,步长 ,因此有
上式两端取极限得
由 知, ,即 ,与算法步骤0中 矛盾,故 。因此算法4.1是全局收敛的。
定理5.2 (局部二次收敛)设矩阵A行满秩且 是算法4.1产生的迭代点列 的任意聚点,若 都是非奇异的,则 ,且 。
证明:类似文献 [10] 中定理8的证明可得此结论,在此省略。
文章引用
梁晓娟. 二阶锥规划基于新价值函数的新光滑牛顿算法
A New Smoothing Newton Algorithm Based on the New Valued Function for Se-cond-Order Cone Programming[J]. 运筹与模糊学, 2019, 09(03): 215-221. https://doi.org/10.12677/ORF.2019.93024
参考文献
- 1. Buss, M., Hashimoto, H. and Moore, J.B. (1996) Dexterous Hand Grasping Force Optimization. IEEE Transactions on Robotics and Autimation, 12, 406-418. https://doi.org/10.1109/70.499823
- 2. Beatriz, L., Antonio, M. and Joaquin, S. (2014) Robot Grasping Foundations. From Robot to Human Grasping Simulation, 19, 15-31. https://doi.org/10.1007/978-3-319-01833-1_2
- 3. Lobo, M.S., Vandenberghe, L., Boyd, S. and Lebret, H. (1998) Applications of Second-Order Cone Programming. Linear Algebra and Its Application, 284, 193-228. https://doi.org/10.1016/S0024-3795(98)10032-0
- 4. Andersen, K.D., Christiansen, E. and Overton, M.L. (1998) Computing Limit Loads by Minimizing a Sum of Norms. SIAM Journal on Scientific Computing, 19, 1046-1062. https://doi.org/10.1137/S1064827594275303
- 5. Faraut, J. and Koranyi, A. (1994) Analysis on Symmetric Cone Oxiord. Clarendon Press, Oxford.
- 6. Alizadeh, F. and Goldfarb, D. (2003) Second-Order Cone Programming. Mathematical Programming, 95, 3-51. https://doi.org/10.1007/s10107-002-0339-5
- 7. Sun, D.F. and Sun, J. (2005) Strong Semismoothness of the Fischer-Burmeister SDC and SOC Complementarity Functions. Mathematical Programming, 103, 575-581. https://doi.org/10.1007/s10107-005-0577-4
- 8. Hayashi, S., Yamashita, N. and Fukushima, M. (2005) A Com-bined Smoothing and Regularization Method for Monotone Second-Order Cone Complementarity Problems. SIAM Journal on Optimization, 15, 593-615. https://doi.org/10.1137/S1052623403421516
- 9. Fukushima, M., Luo, Z.Q. and Tseng, P. (2001) Smoothing Functions for Second-Order Cone Complementarity Problems. SIAM Journal on Optimization, 12, 436-460. https://doi.org/10.1137/S1052623400380365
- 10. Qi, L, Sun, D, Zhou, G. (2000) A New Look at Smoothing Newton Methods for Nonlinear Complementarity Problems and Box Constrained Variational Inequalities. Mathematical Programming, 87, 1-35. https://doi.org/10.1007/s101079900127