Operations Research and Fuzziology
Vol.
10
No.
03
(
2020
), Article ID:
36833
,
5
pages
10.12677/ORF.2020.103017
The Construction of Some Classes of Minimally t-Tough Graphs
Huili Tong, Zongtian Wei
Department of Mathematics, Xi’an University of Architecture and Technology, Xi’an Shaanxi

Received: Jul. 9th, 2020; accepted: Jul. 24th, 2020; published: Jul. 31st, 2020

ABSTRACT
A graph G is minimally t-tough if the toughness of G is t and the deletion of any edge from G decreases the toughness. Constructing a minimally t-tough graph and studying its structural characteristics are of great significance in theory and applications. This paper proves that several kinds of Cartesian product graphs and line graphs are minimally t-tough and also construct a class of k-regular, and minimally k/2-tough graphs.
Keywords:Toughness, Minimally t-Tough Graph, Cartesian Product Graph, Line Graph, Regular Graph

几类极小t-坚韧图的构造
同会利,魏宗田
西安建筑科技大学理学院,陕西 西安

收稿日期:2020年7月9日;录用日期:2020年7月24日;发布日期:2020年7月31日

摘 要
若图G的坚韧度为t,且删除G中任意一条边后坚韧度减小,则称图G是极小t-坚韧的。构造极小t-坚韧图并研究其结构特性在理论和应用上都具有重要意义。证明了几类笛卡尔积图和线图的极小t-坚韧性,并构造出一类k-正则的极小k/2-坚韧图。
关键词 :坚韧度,极小t-坚韧图,笛卡儿积图,线图,正则图

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1973年,Chvátal [1] 首次提出坚韧度的概念,用于研究图的哈密尔顿性。后来,坚韧度成为一个重要的网络抗毁性参数。
定义1 [1] 设G是一个非完全连通图,其坚韧度定义为
。
如果 ,则称 为G的一个坚韧集,简称t-集。
定义2 [1] 设G是一个图, 为G的连通分支数。若对于G的任意点割集S,有 ,其中t是正实数,则称图G是t-坚韧的。
Chvátal同时研究了图的坚韧度和哈密尔顿性的关系,提出了一个关于坚韧度的著名猜想:存在一个确定的正数 ,任何 -坚韧图都是哈密尔顿图 [1]。2006年,Bauer在文献 [2] 中综述了坚韧度和周长的关系、2-坚韧猜想的反证明、因子、特殊图类、计算复杂度,以及与坚韧度相关的各种结果。
Broersm于1999年首次提出极小t-坚韧图的概念 [3]。
定义3 [3] 若图G的坚韧度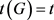 ,且每一个支撑真子图H的坚韧度
,则称G是极小t-坚韧的。
,且每一个支撑真子图H的坚韧度
,则称G是极小t-坚韧的。
换言之,删除G中任意一条边e,图G的坚韧度减小,就说这个图G是极小t-坚韧的。
Katona给出了一些极小t-坚韧图顶点度的上界,并证明了每个极小1-坚韧图的无爪图是一个圈 [4]。2018年,Katona等构造出几类特殊的极小t-坚韧图,并证明了,对于任意正整数t以及任意正有理数 ,极小t-坚韧图的判定问题是DP-完备的 [5] [6]。
极小t-坚韧图具有重要的结构特性与研究意义,然而目前得到的极小t-坚韧图研究成果并不多。因此本文对极小t-坚韧图进行了研究,主要研究了几类笛卡尔积图和线图的极小t-坚韧性,并构造了一类k-正则的极小k/2-坚韧图。文中提及的图均为简单无向图,未加说明的概念和术语见文献 [7]。
2. 几类特殊的极小t-坚韧图
2.1. 笛卡尔积图的极小t-坚韧性
本节主要研究几类常见的笛卡儿积图,证明了完全图与完全图,路与圈的笛卡儿积图是极小t-坚韧的。
定义4设 和 是两个点不交的简单图, 和 的笛卡尔积 是一个简单图,其中 ,并且对 ,, ,且 或者 且 。
引理1 [8] 设 是两个完全图的笛卡尔积,则 。
引理2 [9] 设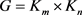 ,其中
,则
,其中
,则
1) G是 -正则的;
2) G是 -连通的。
定理1设 是两个完全图,则 是极小 -坚韧的。
证明由引理1知,
。再由引理2,容易知道,对
的任意一点
w,其邻点集即为
的一个t-集,且
,。设
是
的任意一条边,记 ,则有
。令S为u在H中的邻点集,则有
,。
,则有
。令S为u在H中的邻点集,则有
,。
这表明
由定义3即得, 是极小 -坚韧的。
定理2设 , 分别表示路和圈,其中m为奇数,则 是极小 -坚韧的。
证明明显地, 是3-正则图。设 ,,且在 中,点i的邻点是 和 ,其中 ,并且关于模m同余。记 ,则由
坚韧度的定义,易知
是
的一个t-集,
。设
是
的任意一条边,则在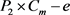 中,
均为2度点。因为
,,所以有
。故结论成立。
中,
均为2度点。因为
,,所以有
。故结论成立。
当 或m为偶数时, ,所以 不一定是极小t-坚韧图。
2.2. 轮形图的极小t-坚韧性
定义5设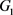 和
是两个点不交的图,
和
的联图,记为
和
是两个点不交的图,
和
的联图,记为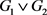 ,是指在
中将
的每个顶点与
的每个顶点之间用一条边连接起来所得到的图。
,是指在
中将
的每个顶点与
的每个顶点之间用一条边连接起来所得到的图。
定义6称 和 的联图 为轮形图,记为 。 中的点称为 的中心,与该点关联的边称为辐条。
定理3轮形图 是极小3/2-坚韧的。
证明由轮形图的结构易知,其中心和 上任意两个不相邻的点构成一个t-集,故有
。
对于任意的 ,考虑以下两种情形。
情形1 。设 ,则在 中, 均为2度点。因为 ,所以 。
情形2 。用v表示e在圈 上的任一端点,v为2度点。与情形1同理,可知 。
综上所述,结论成立。
2.3. 线图的极小t-坚韧性
本节主要讨论三类线图的极小t-坚韧性,证明了路,圈,完全二部图的线图是极小t-坚韧的。
定义7一个图G的线图用 来表示,它的顶点集是G的边集, 中任意两点之间是相邻的,当且仅当G中对应的边是相邻的。
引理3 [5] 树T是极小 -坚韧的弦图。
定理4设 是n阶路,则其线图 是极小1/2-坚韧的。
证明由线图的定义, 是 阶的路。由引理3, 是极小1/2-坚韧的。
定理5设 是n阶圈,则其线图 是极小1-坚韧的。
证明由圈的结构和坚韧度的定义易知,n阶圈 是极小1-坚韧的。又因为 ,所以 是极小1-坚韧的。
完全二部分图的线图 是两个完全图的笛卡尔积,因此有如下结论:
定理6设 是完全二部分图,则其线图 是极小 -坚韧的。
3. 一类极小t-坚韧正则图的构造
本节以轮形图为基础,构造了一类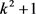 阶的k-正则的极小k/2-坚韧图。
阶的k-正则的极小k/2-坚韧图。
定义8设 是轮形图,将中心点之外的每个顶点都用一个k阶团替换,记这些团为 ,任意两个团 和 之间恰有一条边相连,每个团中的每个顶点有且仅有一个邻点不在这个团中。将所得到的图记为 ,则 是 阶的k-正则图。图1给出的是一个例子 。
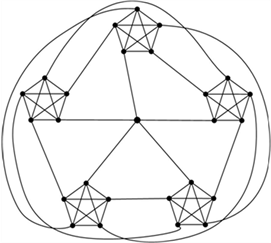
Figure 1. A 5-regular graph with order 26
图1. 一个26阶的5-正则图
定理7由定义8所构造的图 是 阶k-正则的极小k/2-坚韧图,其中 。
证明因为 是 阶k-正则图,则对 的任意一点u,其邻点集 为 的一个t-集,且 ,,即 。设 是 的任意一条边,则在 中, 。令S为u在 中的邻点集,则 ,。易知S是 的一个t-集,从而
。
所以, 是极小k/2-坚韧的。
4. 总结
坚韧度是用来刻画网络抗毁性的一个重要参数。坚韧度与图的结构、哈密尔顿性结合的研究一直是图论中的热点问题。本文证明了几类笛卡尔积图和线图是极小t-坚韧的,并且构造出一类k-正则的极小k/2-坚韧图。极小t-坚韧图是大量存在的,但是找到这些图比较困难。有关极小t-坚韧图的构造与分类,仍有很多问题值得深入研究。
文章引用
同会利,魏宗田. 几类极小t-坚韧图的构造
The Construction of Some Classes of Minimally t-Tough Graphs[J]. 运筹与模糊学, 2020, 10(03): 167-171. https://doi.org/10.12677/ORF.2020.103017
参考文献
- 1. Katona, G.Y. and Varga, K. (2018) Minimally Toughness in Special Graph Classes. arXiv:1802.00055.
- 2. Katona, G.Y., Kovács, I. and Varga, K. (2017) The Complexity of Recognizing Minimally Tough Graphs. arXiv:1705.10570.
- 3. Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Applications. Macmillan London and Elsevier, New York. https://doi.org/10.1007/978-1-349-03521-2
- 4. Chvatal, V. (2006) Tough Graphs and Hamiltonian Circuits. Discrete Mathe-matics, 306, 910-917. https://doi.org/10.1016/j.disc.2006.03.011
- 5. Chvátal, V. (1973) Tough Graphs and Hamiltonian Circuits. Discrete Mathematics, 5, 215-228. https://doi.org/10.1016/0012-365X(73)90138-6
- 6. Bauer, D., Broersma, H. and Schmeichel, E. (2006) Toughness in Graphs—A Survey. Graphs and Combinatorics, 22, 1-35. https://doi.org/10.1007/s00373-006-0649-0
- 7. Broersma, H., Eng-bers, E. and Trommel, H. (1999) Various Results on the Toughness of Graphs. Networks: An International Journal, 33, 233-238. https://doi.org/10.1002/(SICI)1097-0037(199905)33:3<233::AID-NET9>3.0.CO;2-A
- 8. Gunther, G. and Hartnell, B.L. (1991) On m-Connected and k-Neighbour-Connected Graphs. Graph Theory, Combinatorics, and Applications, 2, 585-596.
- 9. Katona, G.Y., Soltész, D. and Varga, K. (2018) Properties of Minimally t-Tough Graphs. Discrete Mathematics, 341, 221-231. https://doi.org/10.1016/j.disc.2017.08.033