Hans Journal of Wireless Communications
Vol.07 No.05(2017), Article ID:22679,8
pages
10.12677/HJWC.2017.75019
Node Scheduling Optimization Algorithm in Heterogeneous Ad Hoc Networks Based on MIMO
Wanmei Feng
School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou Guangdong

Received: Oct. 24th, 2017; accepted: Nov. 7th, 2017; published: Nov. 15th, 2017

ABSTRACT
Multiple-input and multiple-output (MIMO) can obviously improve transmission reliability and bandwidth efficiency in wireless networks. The nodes in heterogeneous Ad Hoc networks enable to communicate directly without wired connections, making up the lack of communication with fixed network infrastructures. Therefore, heterogeneous Ad Hoc networks combined with MIMO techniques becomes one of the research hotspots in academia. However, in heterogeneous Ad Hoc networks based on MIMO, different transmitter-receiver pairs transmit data streams by different links which have the effect of co-channel interference. A good scheduling algorithm plays an important part in reducing the co-channel interference. According to the characteristics of heterogeneous Ad Hoc networks and the contention regions between links, we propose node scheduling optimization algorithm to obtain resource allocation (rate). Based on different rate of different links, transmitters can choose the optimum receivers to transmit data streams via node scheduling. The results of the experience proof that node scheduling optimization algorithm can highly improve the system throughput with reducing the effect of co-channel interference.
Keywords:MIMO, Heterogeneous Ad Hoc Network, Node Scheduling, Interference
基于MIMO异构Ad Hoc网络节点调度 优化算法
冯婉媚
华南师范大学物理与电信工程学院,广东 广州
收稿日期:2017年10月24日;录用日期:2017年11月7日;发布日期:2017年11月15日

摘 要
多输入多输出(MIMO)技术在很大程度上提升无线网络的传输可靠性与频谱利用率。异构Ad Hoc网络中的节点不需要有线连接就能够直接通信,从而弥补了固定网络基础设施通信的缺陷。因此,异构Ad Hoc网络结合MIMO技术成为了学术界的一个研究热点。然而,在基于MIMO异构Ad Hoc网络中,不同的发送–接收对之间是通过不同的链路传输数据流,而链路与链路之间会存在共信道干扰的现象。好的节点调度方法对减少链路之间的干扰起很重要的作用。针对异构Ad Hoc网络传输链路特点,本文提出的分布式节点调度优化方法,根据每一条链路与其他链路之间的竞争情况,得到每一条链路的资源分配(rate)。在进行节点调度的过程中,根据不同链路的rate值,发送节点可以选择最优的接受节点传输数据流。实验仿真结果表示,分布式节点调度优化算法能够明显减少共信道干扰现象,从而提升系统的吞吐量。
关键词 :MIMO,异构Ad Hoc网络,分布式节点调度,干扰

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,人们对于互联网与便携式计算机的需求不断增加,进而推进了对于无线移动装置需求的增长。无线Ad Hoc网络是一种由若干无线通信设备组合形成的分布式无线分组网络,具有组网灵活、分布实施、抗毁能力强、快速组网等特点,可作为野战通信、公安、紧急搜救、会议会场、信息家电等的通信网络。无线Ad Hoc网络分为同构Ad Hoc网络与异构Ad Hoc网络。在同构网络中,每个节点的硬件条件相同。与同构Ad Hoc网络不同,异构Ad Hoc网络具有不同节点的优先级传输、信道状态、天线的数量、发送数据流可能不同的特点。因此,异构Ad Hoc网络具有广阔的应用前景,已成为国内外的一个研究热点。
多输入多输出(MIMO)技术是移动通信领域的一项重大突破。在MIMO系统中,每个节点可以具有多个天线。当发射天线的数量不大于接收天线的数量,接受节点就可以正确分离从不同的发射节点发送的独立的数据流。利用这种新的收发机体系结构,多个独立的数据流可以在相同的信道上同时发送,这为大幅度提高无线Ad Hoc网络的容量性能提供一个崭新而有效途径。然而,现有与MIMO技术有关的研究工作大多数都集中在物理层上,如提高系统容量和提高传输可靠性。事实上,一个好的节点调度方案应该在利用MIMO技术优点与优化整体网络性能的同时,还能保留一些分布式接入的性能。因此,在通信网络中应用MIMO技术值得进一步研究,特别是在移动Ad Hoc网络中。
为了提升系统的吞吐量,文献 [1] 提出了基于MIMO的分布式调度算法。在文献 [1] 中,发送节点根据其信道状态、天线的数量、发送数据流的大小等的信息选择合适的传输数据的方式传输数据流给接受节点。然而,文献 [1] 中的分布式调度算法并没有考虑共信道干扰对节点调度的影响。在自组织网络中,发送节点向接收节点发送数据流经过的一段物理路线称为链路,每条链路都是用来传送数据流。然而,在现实生活中,链路与链路之间可能会存在竞争的情况(在一定的范围内) [2] ,这样就会对数据包的传输造成影响。当一条链路与其他链路的竞争情况越大时,对传输数据的干扰就会越大。因此,通过了解每一条链路与其他链路的竞争情况,我们也能够根据每个节点的所有数据流的情况选择相应的更优的接收节点发送数据流,从而大大地减少链路干扰的现象并提高数据传输的可靠性。为了减少链路竞争的现象,文献 [3] 提出了集中式SCMA算法与分布式SCMA算法,针对传输链路之间的干扰提供了优化的考虑。然而,文献 [3] 提出的节点调度算法没有考虑在异构Ad Hoc网络中节点调度的问题。本论文结合异构Ad Hoc网络特点,考虑传输链路之间的共信道干扰的现象,提出了分布式节点调度优化算法。仿真结果表明,分布式节点调度优化方法能够明显减少共信道干扰的现象,提升系统的吞吐量。
2. 基本原理
2.1. 信道模型
在无线通信中,发射机的天线发出的无线电波可以从不同的路径(直射、反射、绕射、散射)到达接收机,这就是多径传播,而多径传播的环境必然会引起信道的衰落。在多径传播的条件下,当接收机在接收信号的包络服从瑞利分布,此时的信道可以建模成瑞利衰落。当接收机接受的信号的包络服从莱斯分布,此信道可以建模成莱斯衰落 [4] 。瑞利衰落一般是发生在发射机与接收机之间没有直射波信号但存在很多发射波信号的条件下(即离基站较远的情况下)存在的,而莱斯衰落一般是在离基站较近且直射波信号占支配地位的条件下存在的。我们用一个 的矩阵 表示节点 和节点 之间的信道。 和 分别代表的是节点 和节点 的天线数量。信道矩阵中每一个元素可以表示为 [4] :
(1)
其中, 是一个角度,其取值范围是 。 是服从均值为0,方差为 的正态分布。k是直射路径能量与分散路径能量的比值。当 时,该信道是瑞利衰落,当 时该信道是莱斯衰落。每一个发送数据流s用数据流容量𝒷(s)和数据流优先级𝓅(s)两个方面来表示。𝓅(s)表示的是包裹被服务的优先级。数据流容量𝒷(s)表示的是无差错传输的情况下最大程度能够传输的数据流的大小,它与接收信号的信号干扰噪声的比率(SINR)密切相关。𝒷(s)可以由以下的公式得出:
𝒷(s) (2)
代表的是数据流s的发射功率。当发射功率越大的时候,发送信号的信号强度越高,而信号的传输范围也就越远。然而,发射功率的增大就会涉及到能量消耗的问题。因此发射功率的取值范围需要有限制条件。 是一个信道向量。 代表的是噪声系数。 代表的是在接收节点处对接受数据流造成干扰的所有数据流的集合。
2.2. PEO (Perfect Elimination Ordering)和最大派别的识别方法
在图1(a)中,7个节点随机分布在一定的空间范围内,G(V, E)代表节点的网络拓扑图。在G(V, E)中,V代表的是网络中的节点的数量,而E代表的是两个节点之间形成的链路的集合(两个节点在传输范围内)。图1(b)是由图1(a)中的网络节点图转变过来的数据流竞争图G'(V', E', W)。在G'(V', E', W)中,V’代表的是在网络中链路的集合,E'代表的是在G'中任意两个节点之间的边缘,W是每个边缘的权重,代表着两个节点之间的干扰情况。每个节点与其竞争的节点形成竞争区域。从数据流竞争图中可知链路之间的竞争情况以及每条链路所在的派别,而每一条链路可能属于多个不同的派别。每个派别的识别如下:在
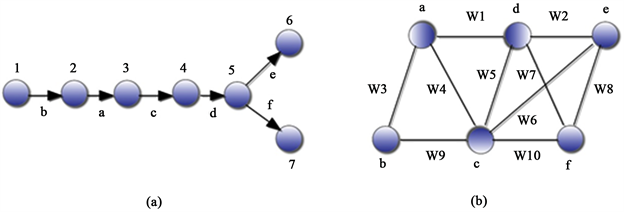
Figure 1. An illustration of network topology. (a) Topology example; (b) Corresponding channel contention
图1. 一个网络拓扑图的举例。(a) 网络节点图;(b) 数据流竞争图
数据流竞争图中,首先通过LexBFS算法 [5] 找出所有的PEO,接着通过Fulkerson and Gross [6] 算法识别所有的最大派别。根据每条链路属于最大派别的情况,链路可以分成红色链路或者白色链路。红色链路是属于两个或者两个以上的最大派别的链路,反之就是白色链路。
2.3. 按比例公平分配资源模型
代表所有能够直接或者间接利用红色链路j牺牲的数据流来发送数据流的链路的集合,当链路 满足以下的条件时,即成为集合 中的元素:
其中,c表示最大派别, 代表链路i所在的最大派别的集合, 代表所有属于竞争区域d中链路的集合, 代表集合 中的元素的个数。
在每一个竞争区域中,根据每一条链路所属最大派别的情况分配占用资源的比例rate [3] 。占用资源的比例反映每一条链路最大占用资源块的程度。当链路i属于红色链路时,rate可以表示为:
当链路为白色链路时,
其中, 代表的是链路 所在的最大派别中的所有链路分配最小的资源,而 代表的是 中所有的成员分配的最小的资源。
2.4. 贫穷节点与富裕节点
根据节点是否能够作为发送节点与接受节点这个特点,所有的节点可分为贫穷节点与富裕节点。贫穷节点可作为发送节点或者接收节点,富裕节点只能够作为接收节点 [1] 。当 成立时,
节点i为能够作为贫穷节点,否则节点i只能够作为富裕节点,其中 , 。 代表节点i的优先级, 代表节点i中所有的数据流的集合,而𝓅(siq)是节点i上第q个数据流的优先级。 是节点i的邻居节点中所有活跃的节点的平均优先级, 代表的是节点i的邻居节点中活跃的节点的集合。 代表的是在节点i中用于传输给邻居节点的数据流的平均优先级, 是一个随机数,其取值范围是 。在 中, 代表的是节点j中的接收限制, 代表的是节点i中所有的邻居节点的集合。
3. 分布式节点调度优化算法
分布式节点调度优化算法的主要思想是:根据每一个节点天线的数量,发送数据流大小,信道状况以及链路之间的共信道干扰等的信息,选择合适的发送–接受对传输数据流,进一步地减少共信道干扰现象,从而提升系统的吞吐量。此算法的主要步骤如下所示:
1) 输入网络拓扑图G(V, E),根据链路之间的竞争情况,将网络拓扑图G(V, E)转变成数据流竞争图G'(V', E', W)。
2) 通过数据流竞争图识别出所有的最大派别,将链路分成红色链路与白色链路。
3) 根据每一条链路所属最大派别的情况分配占用资源的比例。
4) 所有节点分为贫穷节点和富裕节点。
5) 节点调度过程:发送节点根据链路之间的干扰情况以及发送数据包大小选择接收节点传输数据流,但发送节点与接收节点不能是同一个节点。
在节点调度之前,根据(1)-(6)的步骤,把所有节点分成贫穷节点与富裕节点,链路分成红色链路与白色链路。节点调度的过程,如上述步骤(7)所示。然而,两个或者两个以上的节点需要进行数据传送时会产生冲突的现象,CSMA/CA协议能够解决这个问题。发送节点首先把信道状态,发送的数据流的数量,发送节点的ID与接收节点的ID等的信息放入RTS中,并发送给接收节点。ID是用于标识每个节点的,而每个节点都会有一个不同的ID。每一个接收节点可能会收到很多来自不同节点的RTS,而接收节点就会根据每个节点的优先级选择优先级最高的发送节点。当优先级相同的时候,接收节点就会选择ID更高级别的发送节点进行数据传输。接下来,接收节点就会根据发送节点中RTS所包含的信息进行分析,当接收节点发现与发送节点之间存在很长的距离或者发送节点与接收节点之间的信道是严重衰落的信道,那么接收节点就会通过发送CTS给发送节点让其寻找一个更可靠的接收节点。如果接受节点周围的信道状况适合与接受节点通信,接收节点就会把传输方式,接收节点的接收限制,信道状况,还有接收节点的ID等的信息放入CTS中并发送给发送节点。发送节点接收了接收节点的CTS之后,就会确定是否能够与接受节点进行通信。若发送节点与接受节点之间能够允许通信,发送节点就会确定数据的传输方式并开始发送数据流给接受节点。在节点调度的过程中,本算法也考虑到信道环境等的问题,对信道环境差的情况作出相应的处理,进一步提高通信质量。当发现接收节点处于弱信道时,发送节点就会减少一条发射天线从而使得剩下能够用于发送数据流的每一条天线的发射功率增大。当发射功率增大之后,系统的通信质量提高,减少包裹丢失的概率。发送完最高级别的数据流之后,发送节点接着寻找下一个最优的数据流发送给接受节点,如此循环能够把每一个节点的所有数据流尽可能地传输给接受节点。当接收节点全部接受发送节点传输的数据流之后,就会把接收节点的ID,接收数据流的数量,丢失包裹的数目等的信息放入ACK中再发送给发送节点,从而确定接收完毕。
4. 仿真结果
本次仿真中,100个节点随机分布在1250 m × 1250 m的空间中形成无线Ad Hoc网络。在Ad Hoc网络中的每一个节点的天线数量服从均值为4,方差为1的随机分布。每一个节点的传输范围是250 m,且节点可以在空间范围内自由地移动。每一个节点转发的包裹大小是100 bytes,且每一个到达的通信量服从参数为λ的泊松分布。网络认为是静态的。频谱资源的带宽是20 MHZ。每一个传输时隙是2.5 ms。
从图2可以看见,在不考虑干扰的情况下,天线数量增加会提升系统总体的吞吐量。这个是由于在节点数量不变的情况下,总体的天线数量增加就会使得发送数据流的总和增加,系统的吞吐量就会提升。这个同样也是MIMO系统比SISO的系统的吞吐量更大的原因。在考虑到干扰的情况下,当天线数量提升时,分布式节点优化调度算法的系统吞吐量明显提升。
从图3可以看见,在不考虑干扰且空间范围确定的情况下,当增加空间中的节点的数量时,系统的吞吐量会因此相应地增加。这个是由于增加空间中的节点的数量,相应地增加发送节点与接收节点数量,传输的数据流的总量也会增加,进而提升系统的总的吞吐量。在考虑干扰的情况下,当节点数量增加时,分布式节点调度优化算法的系统吞吐量明显提升。
节点的天线数量的方差越大,表明节点的自由度增加时,此时符合异构网络的特点。当自由度(方差)为0时候,此时网络就是同构网络。在同构网络中,所有的节点的天线数量相同。从图4可以看见,节点的天线数的方差增加,系统的吞吐量就会下降。
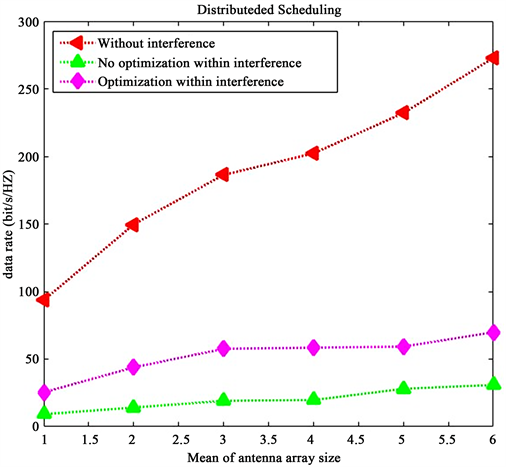
Figure 2. Impact of mean of antenna array size
图2. 天线数量的均值大小的影响
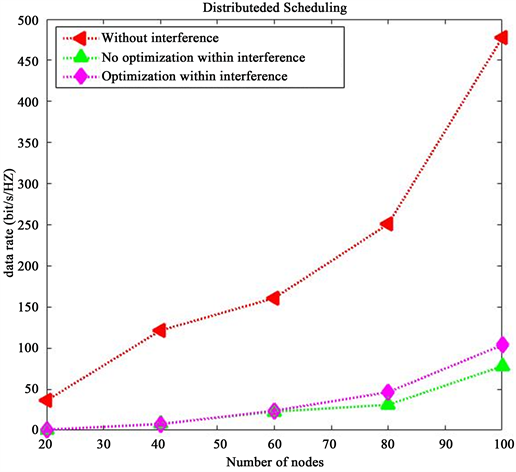
Figure 3. Impact of node density
图3. 节点数量大小的影响
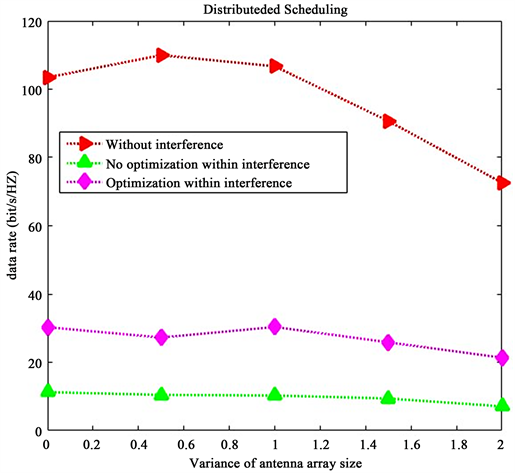
Figure 4. Impact of variance of antenna array size
图4. 天线数量的方差大小的影响
5. 结束语
在节点调度的过程中,传输链路之间存在着共信道干扰的现象,这样会导致通信系统的质量下降。为了改善链路之间的干扰现象,本文提出了分布式节点调度优化算法。此算法在节点调度的过程中,考虑节点的数量,天线的数量,信道状态,发送数据流的数量,共信道干扰等的情况,发送节点选择最优的接收节点发送数据流。与其他调度算法相比,本文提出的分布式节点调度优化方法能够明显提升系统的吞吐量。
致谢
本论文获得华南师范大学研究生创新计划项目资助。
文章引用
冯婉媚. 基于MIMO异构Ad Hoc网络节点调度优化算法
Node Scheduling Optimization Algorithm in Heterogeneous Ad Hoc Networks Based on MIMO[J]. 无线通信, 2017, 07(05): 155-162. http://dx.doi.org/10.12677/HJWC.2017.75019
参考文献 (References)
- 1. Chu, S., Wang, X. and Yang, Y. (2014) Adaptive Scheduling in MIMO-Based Heterogeneous Ad Hoc Networks. IEEE Transactions on Mobile Computing, 13, 964-978. https://doi.org/10.1109/TMC.2013.112
- 2. Nandagopal, T., Kim, T.E., Gao, X., et al. (2000) Achieving MAC Layer Fairness in Wireless Packet Networks. International Conference on Mobile Computing & Networking, Boston, 6-11August 2000, 87-98. https://doi.org/10.1145/345910.345925
- 3. Sundaresan, K., Sivakumar, R., Ingram, M.A., et al. (2004) Medium Access Control in Ad Hoc Networks with MIMO Links: Optimization Considerations and Algorithms. IEEE Transactions on Mobile Computing, 3, 350-365. https://doi.org/10.1109/TMC.2004.42
- 4. Tse, D. and Viswanath, P. (2009) Fundamentals of Wireless Communication. Posts and Telecom Press, Beijing, 1-5.
- 5. Donald, J. and Tarjan, E.R. (1978) Algorithmic Aspects of Vertex Elimination. Siam Journal on Applied Mathematics, 34, 176-197. https://doi.org/10.1137/0134014
- 6. Fulkerson, D.R. and Gross, O.A. (1965) Incidence Matrices and Interval Graphs. Pacific Journal of Mathematics, 15, 835-855. https://doi.org/10.2140/pjm.1965.15.835