Hans Journal of Wireless Communications
Vol.
09
No.
01
(
2019
), Article ID:
28617
,
7
pages
10.12677/HJWC.2019.91001
A Hyperparameter-Free Direction-Finding Algorithm in the Compressive Sensing Framework
Xiangdong Ma, Ming Guo, Xiangyang Wu
Luoyang Electronic Equipment Test Center of China, Luoyang Henan

Received: Jan. 1st, 2019; accepted: Jan. 17th, 2019; published: Jan. 24th, 2019

ABSTRACT
The fully automatic sparsity-parameter estimation algorithms do not require the user to make any hard decision (possibly via trial-and-error) on the values of the hyperparameters, making them more pragmatic in practice. This paper provides a unified interpretation of the existing approaches including covariance matrix fitting (CMF), sparse iterative covariance based estimation (SPICE) and likelihood-based estimation of sparse parameters (LIKES). The point of view taken is that they are all covariance-fitting-based algorithms under different statistical distances. Following this, we present a new covariance-fitting scheme trying to minimize one of the two asymmetrical Itakura-Saito distances. Simulations show that the proposed method appears to be preferable as it outperforms the aforementioned algorithms in general.
Keywords:Spectrum Management, Spectrum Monitoring, Direction Finding, Array Signal Processing
一种基于压缩感知的无需超参数的测向算法
马向东,郭明,吴向阳
中国洛阳电子装备试验中心,河南 洛阳

收稿日期:2019年1月1日;录用日期:2019年1月17日;发布日期:2019年1月24日

摘 要
全自动的稀疏参数估计算法不需要用户对于超参数的数值做出任何艰难的决定(可能是试错而来),因而更加实用。本文给出了现有方法的统一阐释,包括协方差矩阵拟合(CMF)、基于稀疏迭代协方差的估计(SPICE)以及基于似然的稀疏参数估计(LIKES),认为它们全部都是不同统计距离下的基于协方差矩阵拟合的方法。在此基础上,本文提出了一种新的协方差矩阵拟合方案,将两种非对称Itakura-Saito距离的其中一种最小化。计算机仿真表明,本文提出方法相比上述方法的性能具有优势。
关键词 :频谱管理,频谱监测,测向,阵列信号处理

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
频谱监测是频谱管理的重要工具,主要目的是完成对无线电频谱的监测和无线电信号参数的测量,其中,无线电信号的测向是其主要任务之一。现代测向技术包括旋转天线、多普勒、沃森–瓦特、相位干涉仪、相关干涉仪、高分辨率测向等等。本文讨论的是高分辨率测向技术,该项技术主要用来分辨相同频率的多个发射机的信号的方向 [1] 。
代表性的高分辨率测向技术有波束形成法 [2] 和子空间方法 [3] 。近年来,基于压缩感知的方法由于相较前两类方法进一步提升了估计精度而逐渐受到关注 [4] 。从数学上看,测向设备对空间谱的感知是一种欠定方程,即:以比较少的天线单元个数来分辨来自于各个方向的信号的能量。欠定方程的解通常有无穷多个,为了减少解的数量,提高对空间谱的分辨能力,需要对方程施加更多的约束。压缩感知(compressive sensing),亦称为压缩传感,是一种利用未知矢量的稀疏性(sparsity),对解进行约束的方法。稀疏性指的是一个矢量只有少数的几个元素不为零,大多数是零元素。空间谱符合稀疏性这一特征:对于某一个频点/信道而言,空间中只存在有限个方向的同频信号,大部分的方向是没有该频点/信道的信号的。该类方法的最新趋势是摆脱算法用户的人工干预,无需用户设定超参数(hyperparameter)从而实现全自动计算 [5] [6] [7] 。本文的目的即是提出一种基于压缩感知的无需超参数的测向算法,以实现高精度同频信号测向。
2. 数学模型
考虑一个N个天线单元和接收通道组成的测向设备接收到了M个同频窄带信号 ,其导向矢量分别为 ,背景噪声为 。阵列测量矢量由下式给出:
(1)
令
为可以覆盖所有可能入射区域的栅格,并覆盖了(至少是近似覆盖了)上述M个信号的入射角度,相应的导向矢量为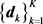 ,其中,
。于是,式(1)可以重新表述为:
,其中,
。于是,式(1)可以重新表述为:
(2)
其中, 代表来自于 方向的可能存在的辐射源的信号。基于压缩感知的到达角估计算法的目标即是从K个可能存在的辐射源中找出M个真实存在的辐射源。
上述问题可以采用约束lp范数最小化方法解决,例如LASSO [8] 、FOCUSS [9] [10] 、l1-ACCV [11] 等等。然而,因为没有用来确定上述方法中涉及的拟合门限、正则化参数等超参数的规则,上述方法在实际应用中常常难以实施。最近,学者们提出了一系列基于协方差矩阵拟合 [12] 的稀疏参数估计方法,由于这些方法不需要设定超参数,因而可以全自动运行。
假设入射信号之间相互独立,背景噪声为空时白噪声,那么阵列协方差矩阵的稀疏表示为:
(3)
其中, 为第k个可能存在的辐射源信号的功率, 为噪声协方差矩阵, 代表共轭转置。为了考虑噪声功率不均匀的情况,可以定义 , , ,所以有:
(4)
同时,对于给定的L组阵列采样 ,阵列采样协方差矩阵的估计公式为:
(5)
2.1. 协方差矩阵拟合算法(CMF)
协方差矩阵拟合算法(CMF)是在均匀噪声功率的假设下,将理论协方差矩阵 与采样协方差矩阵 之间的欧式距离(SED)最小化 [5] ,即
(6)
其中, 为 的特征值。如果我们使用非均匀噪声功率模型,上述问题将会简化为:
(7)
2.2. 基于稀疏迭代协方差的估计(SPICE)
SPICE算法 [6] 实际上是将两种高斯分布 和
之间的Jeffreys距离(亦称为对称Kullback-Leibler距离) [13] 最小化:
和
之间的Jeffreys距离(亦称为对称Kullback-Leibler距离) [13] 最小化:
(8)
对于非高斯分布而言,上述拟合公式仍然是一种度量两个协方差矩阵差异的优秀标准。论文 [6] 中有关随机相位信号的仿真结果证明了这一点。
2.3. 基于似然的稀疏参数估计(LIKES)
LIKES算法 [7] 使用的是高斯最大似然(GML)标准:
(9)
其中, 。论文 [14] 证明了对于参数估计而言,GML代价函数最小化等价于两种高斯分布 和 之间的两种非对称Itakura-Saito距离(ISD)的其中一种最小化,由下式给出:
(10)
和式(8)一样,式(9)中的拟合标准对于非高斯分布来说仍然有效。然而,式(9)中的优化问题不是凸优化问题,需要利用SPICE算法进行迭代优化 [7] 。
3. 本文提出的协方差矩阵拟合方案
本文提出利用另外一种非对称Itakura-Saito距离(ISD)用作拟合标准,即
(11)
经过简单的计算可知,
(12)
容易验证,对于 , ,有 。因此, 的最小化问题属于“max-det”凸优化问题 [15] 。如同LIKES方法,该方法也属于最大似然方法 [16] 。
有关鲁棒自适应波束形成的研究表明,直接使用采样协方差矩阵的逆矩阵 可能会导致算法性能下降,尤其是在采样点数较小的情况下 [14] 。为了解决这一问题,我们将 替换为基于广义线性组合(GLC) [17] 的收缩型增强估计:
(13)
其中,
(14)
因此,本文提出的方法可以表述为:
(15)
式(15)可以利用“max-det”问题专用数学工具MAXDET [18] 、通用凸优化数据工具CVX [19] 等来实现优化计算。例如,当使用CVX数学工具时,可以定义:
(16)
(17)
(18)
那么,式(15)的CVX优化代码为:
cvx_begin quiet
cvx_precision best
cvx_expert true
variable p(K+N,1)
minimize (c'*p-log_det(D*diag(p)*D'))
subject to
p >= zeros(K+N,1);
cvx_end
对矢量 进行局部极值搜索,即可获得测向结果。
4. 计算机仿真
本节给出计算仿真示例来验证本文提出算法的性能。仿真场景为一个10阵元的均匀线性阵列(阵列间距为半个波长),接收三个同频率的远场窄带信号(分别来自−5˚,15˚和25˚),背景噪声为加性高斯白噪声。使用步进为0.1˚的均匀栅格来覆盖可能的入射角度(−90˚,90˚],即 。图1展示了本文提出的算法与CMF、SPICE、LIKES方法的均方根误差(RMSE)随着信噪比(SNR)变化的曲线,其中采样点数固定为200。图2则展示了上述算法的RMSE随着采样点数变化的曲线,其中信噪比固定为10 dB。图1和图2的结果均为300次蒙特卡洛随机实验的平均结果,RMSE利用下式进行计算:
(19)
其中, 、 、 分别是对 、 、 的第n次估计结果。
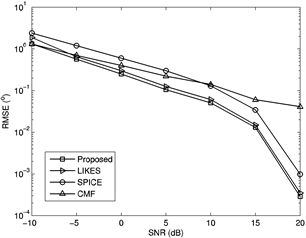
Figure 1. RMSE versus varied SNR
图1. 均方根误差随信噪比的变化曲线
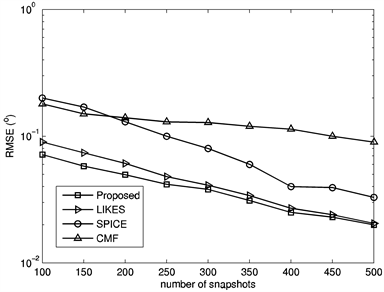
Figure 2. RMSE versus varied numbers of samples
图2. 均方根误差随采样数的变化曲线
从图1和图2可以看出,本文提出算法在参与比较的算法中是最准确的。它的性能与LIKES算法相仿,略有提升。这两种算法是基于非对称Itakura-Saito距离的两个相反的方向:一个衡量的是 到 的收敛度,另一个衡量的是 到 的收敛度。需要指出的是,LIKES算法的优化是一个非凸优化问题,在某些随机实验中难以做到全局收敛,而本文算法的优化是一个凸优化问题,其全局收敛性得到了保证。这最终造成了两者在角度估计精度上的差别。
5. 结论
本文针对数种基于协方差拟合的稀疏系数估计算法,给出了一种统一的基于收敛距离的解释,并在此基础上提出了一种利用Itakura-Saito距离的新方法,该方法的估计性能优于参与比较的方法。鉴于收敛距离的种类繁多,在将来还有许多研究需要做。举例来说,Bhattacharyya距离 [20] 和Wasserstein度量 [21] 不需要用户指定参数,具有作为拟合标准的潜力。
文章引用
马向东,郭 明,吴向阳. 一种基于压缩感知的无需超参数的测向算法
A Hyperparameter-Free Direction-Finding Algorithm in the Compressive Sensing Framework[J]. 无线通信, 2019, 09(01): 1-7. https://doi.org/10.12677/HJWC.2019.91001
参考文献
- 1. ITU (2011) Spectrum Monitoring Handbook. ITU, Geneva.
- 2. Capon, J. (1969) High-Resolution Frequency-Number Spectrum Analysis. Proceedings of the IEEE, 57, 1408-1418.
https://doi.org/10.1109/PROC.1969.7278 - 3. Schmidt, R.O. (1986) Multiple Emitter Location and Signal Parameter Estimation. IEEE Transactions on Antennas and Propagation, 34, 276-280.
https://doi.org/10.1109/TAP.1986.1143830 - 4. Malioutov, D., ?etin, M. and Willsky, A. (2005) A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays. IEEE Transactions on Signal Processing, 53, 3010-3022.
https://doi.org/10.1109/TSP.2005.850882 - 5. Yardibi, T., Li, J., Stoica, P., et al. (2008) Sparsity Constrained Deconvolution Approaches for Acoustic Source Mapping. Journal of Acoustical Society of America, 123, 2631-2642.
https://doi.org/10.1121/1.2896754 - 6. Stoica, P., Babu, P. and Li, J. (2011) SPICE: A Sparse Covariance-Based Estimation Method for Array Signal Processing. IEEE Transactions on Signal Processing, 59, 629-638.
https://doi.org/10.1109/TSP.2010.2090525 - 7. Stoica, P. and Babu, P. (2012) SPICE and LIKES: Two Hyperparameter-Free Methods for Sparse-Parameter Estimation. Signal Processing, 92, 1580-1590.
https://doi.org/10.1016/j.sigpro.2011.11.010 - 8. Tibshirani, R. (1996) Regression Shrinkage and Selection via the Lasso. Journal of Royal Statistical Society: Series B (Statistical Methodology), 58, 267-288.
https://doi.org/10.1111/j.2517-6161.1996.tb02080.x - 9. Gorodnitsky, I.F. and Rao, B.D. (1997) Sparse Signal Reconstruction from Limited Data Using FOCUSS: A Re-Weighted Minimum Norm Algorithm. IEEE Transactions on Signal Processing, 45, 600-616.
https://doi.org/10.1109/78.558475 - 10. Cotter, S.F., Rao, B.D., Engan, K., et al. (2005) Sparse Solutions to Linear Inverse Problems with Multiple Measurement Vectors. IEEE Transactions on Signal Processing, 53, 2477-2488.
https://doi.org/10.1109/TSP.2005.849172 - 11. Xu, D.Y., Hu, N., Ye, Z.F., et al. (2012) The Estimate for DOAs of Signals Using Sparse Recovery Method. Proceedings of the 37th IEEE International Conference on Acoustics, Speech, and Signal Processing, Kyoto, 2573-2576.
https://doi.org/10.1109/ICASSP.2012.6288442 - 12. Ottersten, B., Stoica, P. and Roy, R. (1998) Covariance Matching Estima-tion Techniques for Array Signal Processing Applications. Digital Signal Processing, 8, 185-210.
https://doi.org/10.1006/dspr.1998.0316 - 13. Kullback, S. (1997) Information Theory and Statistics. Dover Edition. Dover, New York.
- 14. Bensaid, S. and Slock, D. (2012) Blind Audio Source Separation Exploiting Periodicity and Spectral Envelops. Pro-ceedings of International Workshop on Acoustic Signal Enhancement, Aachen.
- 15. Vandenberghe, L., Boyd, S. and Wu, S.P. (1998) Determinant Maximization with Linear Matrix Inequality Constraints. SIAM Journal on Matrix Analysis and Applications, 19, 499-533.
https://doi.org/10.1137/S0895479896303430 - 16. Landi, L., De Maio, A., De Nicola, S., et al. (2008) Knowledge-Aided Covariance Matrix Estimation: A MAXDET Approach. IET Radar, Sonar & Navigation, 3, 341-356.
https://doi.org/10.1109/RADAR.2008.4720823 - 17. Li, J., Du, L. and Stoica, P. (2008) Fully Automatic Computation of Di-agonal Loading Levels for Robust Adaptive Beamforming. Proceedings of the 33rd IEEE International Conference on Acoustics, Speech, and Signal Processing, Las Vegas, 2325-2328.
- 18. Wu, S.P., Vandenberghe, L. and Boyd, S. (1996) MAXDET: Software for Determinant Maximization Problems. Information Systems Laboratory, Stanford University, Stanford.
- 19. Grant, M. and Boyd, S. (2012) CVX: MATLAB Software for Disciplined Convex Programming, Version 2.0 Beta. http://cvxr.com/cvx
- 20. Bhattacharyya, A. (1943) On a Measure of Divergence between Two Statistical Populations Defined by Their Probability Distributions. Bulletin of the Calcutta Mathematical Society, 35, 99-109.
- 21. Zolotarev, V.M. (1984) Probability Metrics. Theory of Probability and Its Applications, 28, 278-302.
https://doi.org/10.1137/1128025