Hans Journal of Data Mining
Vol.
09
No.
02
(
2019
), Article ID:
28838
,
9
pages
10.12677/HJDM.2019.92002
Application of Likelihood Ratio Scanning Method in Multiple Mean Changes in Long Memory Time Series
Qiongyao Xu, Yuhong Xing
School of Mathematics and Statistics, Qinghai Normal University, Xining Qinghai
Received: Jan. 23rd, 2019; accepted: Feb. 6th, 2019; published: Feb. 13th, 2019

ABSTRACT
Based on likelihood ratio scanning method (LRSM), this paper studies the multiple change point problem of mean in piecewise stationary long memory time series. Through numerical simulation, it is found that applying the LRSM directly to long memory time series will lead to inaccurate detection of the number and location of change points. By revising the residual estimation method of likelihood function parameters in LRSM, a new LRSM is proposed which is suitable for long memory time series. The effectiveness and practicability of the improved method are proved by numerical simulation and actual data analysis.
Keywords:Long Memory Time Series, Mean Change Points, Likelihood Ratio Scanning Statistics
似然比扫描法在长记忆时间序列均值多变点中的应用
徐琼瑶,邢玉红
青海师范大学数学与统计学院,青海 西宁
收稿日期:2019年1月23日;录用日期:2019年2月6日;发布日期:2019年2月13日

摘 要
本文基于似然比扫描方法,研究分段平稳长记忆时间序列中的均值多变点问题,通过数值模拟发现,直接将似然比扫描方法应用于长记忆时间序列会导致对变点个数及位置的检测不准确。通过改变似然比扫描方法中似然函数参数的残差估计方法,提出了一种适合长记忆时间序列的似然比扫描方法,数值模拟和实际数据分析证明了改进后的方法的有效性和实用性。
关键词 :长记忆时间序列,均值多变点,似然比扫描统计量

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
变点问题起源于page [1] 1954年在Biometrika上发表的一篇有关于连续抽样检验的文章,自此,变点问题引起了众多统计学者的关注。特别是近几十年以来,变点的检测问题已经成为统计学,计量经济学等领域研究的热点问题。产品质量的变化,股市的异常波动,气候的变化等系统的波动问题均可以被抽象为变点问题,这使得变点检测问题在质量监控、金融 [2] 、气候 [3] 、医学 [4] 等领域都有实际的应用背景,因此,研究变点的检测问题不仅具有重要的理论意义,更具有重要的实际意义。
有很多的学者对单变点的情况进行了实验研究,Kokoszka等 [5] [6] [7] 利用累积和CUSUM统计量研究了ARCH变点问题,Kim等 [8] [9] 在CUSUM统计量的基础上对GARCH模型的变点问题进行了研究。马建琦等 [10] 提出了一些新的比率型统计量来检验长记忆时间序列中的均值变点。但是在实际生活中,变点的数量并非有且仅有一个,这使得研究者必须要去检测多变点的存在问题,秦瑞兵等 [11] 提出了检验独立随机序列均值多点的非参数方法,Chen [12] [13] 等利用滑动比率法研究了时间序列中持久性多变点的检验和估计问题。此外,通过优化一个特定的目标函数来寻找变点是解决这一问题的有效办法,例如最小二乘准则,贝叶斯信息准则BIC (Yao等 [14] 和Lavielle和Ludena [15] )。值得注意的是,随着样本量的增长,检测到的可能是变点的数量会呈指数增长,这使得优化函数计算量的难度和复杂度都会大大提升。为了解决这一难题,许多学者也提出了一些解决办法,例如Davis等人 [16] 在2006年提出的遗传算法,Killick等人 [17] 在2012年提出的PELT方法,但是优化难题依然存在,特别是遗传算法涉及到很多的调优参数,操作起来困难重重;另外,PELT方法的计算复杂度接近n2,这里n是样本量。
为了避免在优化上遇到的难题,一个比较受欢迎的解决方法就是二分法,二分法可以追溯到上世纪80,90年代(Vostrikova [18] 和Bai [19] ),二分法在均值多变点和方差多变点的检测和估计上也有很多的应用,具体可以参见文献Inclan和Tiao [20] 和Berkes等人 [21] 。之后,Fryzlewicz在2014年在检测均值变点的问题上对二分法做了一个很重要的扩展,可见文献 [22] ,扩展之后的二分法被命名为WBS;此外,Yau和Zhao提出了似然比扫描方法(LRSM),可见文献 [23] ,与WBS,PELT等方法相比,似然比扫描方法不仅在计算难度上从n2降低到了 ,而且提高了变点估计的精度。遗憾的是,该方法仅仅是用在了自回归序列上,在日常生活中,很多数据都具有长记忆性,因此,将该方法拓展到长记忆时间数据的应用上刻不容缓。
本文主要研究似然比扫描方法在检测长记忆时间序列均值多变点中的应用,数值模拟发现直接将该方法应用到长记忆时间序列中并不能准确地检测到变点,改变似然比扫描法方法中似然函数参数残差的估计方法,变点个数的估计以及变点位置的检测在准确度上有所提高,最后通过数值模拟和实际数据的分析来证明改进后的方法的有效性。本文的主体框架如下:第2节详细介绍似然比扫描方法,第3节介绍新方法,第4节通过数值模拟来说明将似然比扫描方法直接应用到长记忆时间序列中的不足,以及新方法的有效性,实际数据的分析放在第5节。
2. 似然比扫描方法
2.1. 基本设定和假设
假设观测序列 可以被分割成 段平稳的自回归序列,令 ,j表示变点个数,用 表示序列从第j段跳跃到第 段突变点的位置(第j个变点的位置)。令 , ,那么第j
段平稳自回归序列的表达式可以由下式给出:
, ,
这里 表示平稳自回归过程,满足
为独立同分布的白噪声序列,且均值为0,方差为1。
假设2.1.1 用 表示第j段自回归序列的参数向量,假定所有的 都是紧致空间 的内部点。
假设2.1.2 假设所有被分割成的每一段自回归序列的阶数都是有限的,这里把每一段自回归序列的最大阶数用整数 来表示。
假设2.1.3 假设所有被分割成的每一段自回归序列都相互独立。
在接下来的这一小节中,介绍用似然比扫描方法估计多变点的三个步骤。
2.2. 用似然扫描方法估计变点的三个步骤
第一步:
定义在t点的扫描窗口
,
扫描窗口对应的观测值为
这里 ,h称为扫描窗口的窗口半径,这里假定在样本量小于等于800时,h的取值为25,当样本量大于800时,我们把h的取值定义为 ,这里n是样本量。在样本量大于800时,本文取 。
为了检测扫描窗口中的变点,似然比统计量成为一个很自然的选择。任意给定一个样本 ,定义拟似然统计量
(1)
这里 是在 之前给定观测值的条件密度函数,在 的情况下, 。那么,扫描窗口 的似然比扫描统计量就可以定
义为
这里 , 和 的定义方式与表达式(1)类似,但是对应的观测值分别为 , 和 。
因为被分割的每一段序列所拟合的自回归模型 都可以表示成 ,这里就把每一段的序列在拟合成自回归模型时,把所有的阶数定为 ,为了提高模型的实际性能,可以使用信息准则(如Akaike信息准则AIC或者是BIC信息准则)分别对 , 和 三个估计量的自回归模型的阶
进行估计。
用 统计量扫描所有的观测值可以得到一系列的似然比扫描统计量
。如果t是变点,那么 的值会趋向于变大,由于选择的窗口长度为2h,
那么也就意味着在每一个窗口2h的长度中,变点的个数最多只有一个,因此,通过估计局部变点的位置,可以获得一系列可能是整个序列上的变点的所有疑似变点,定义为:
当 或者是 时, ,如果 在以点m为中心的窗口 中达到最
大值,就把m点当做是一个局部变点。
第二步:
通过模型选择的方法从第一步得到的疑似变点的 集合中找到正确的变点。
由于在第一步估计变点的问题上可能存在过估计的问题,所以在第二步要选择一个最小化准则来优化在第一步当中得到的变点个数及位置,本文采用的最小化准则是拥有较好经验性能够的最小描述长度(MDL)准则,由下式给出:
其中, 表示在第一步中得到的变点, 表示被分割成的每一段序列的样本量, 是每一段序列上估计 的自回归模型的阶数。
通过对集合 中的变点进行最小化准则的优化后,可以得到优化后的变点,其表达式如下:
第三步:
对第二步中得到的变点集合 中的变点进行最终估计。
定义第j个变点 的扩展扫描窗口
其对应的观测值为
令 ,对于 ,定义最后的变点估计量为:
这里 ,同理可以得到 的定义。
3. 对似然比扫描方法的改进
本文对似然比扫描方法的改进之处在于对 的估计方法上,似然比扫描方法是在给定序列为自回归序列的情况下提出的,所以在估计 时采用的是通过拟合自回归模型得到的残差序列进行估计,而现在使用的数据为带有长记忆性的时间序列,所以,再用拟合自回归模型的方式得到残差序列进而估计 的值必然不合适。因此,必须考虑长记忆时间序列模型( 模型)
,
其中n是样本容量,L是滞后算子, 为长记忆参数, 为独立同分布的随机变量,且满足 , ,本文只考虑平稳的长记忆时间序列,即 。
而对于长记忆时间序列残差的估计方法在R语言程序中由专门的程序包,除此之外,不再对似然比扫描方法做任何改变,因此,原方法的所有理论结果都适用于经过改善过的新方法,所有的理论证明都可以参见文献 [23] ,在此不做多余阐述。
4. 数值模拟
本小节通过数值模拟来表现直接将似然比扫描方法应用到长记忆时间序列中的不足,以及检验所提新方法的有效性,所有模拟实验通过R语言程序3.5.0版本实现,数据由 模型生成,样本量分别取600,800和1000,长记忆参数 分别取0.1,0.2,0.3和0.4,变点位置 ,分别设置没有变点,有一个变点,有两个变点三种情况进行模拟实验,在变点前后,跳跃度设置为1,在设置成一个变点的情况下, 取0.5;在设置成两个变点的情况下, 取0.5和0.75,S.D表示标准差,MSE表示均方误差,所有模拟结果都经过1000次循环得到。
表1给出了原方法与新方法在样本量分别为600,800和1000,不设置任何变点的情况下,在1000次模拟实验中,正确检测出没有变点的次数,从表中可以看出,随着样本量的增大,检测效果越好,总体上看,新方法与原方法的检验效果不相上下。
Table 1. Correctly detect the number of times that there is no change point
表1. 正确检测出没有变点的次数
表2给出了原方法与新方法在样本量分别为600,800和1000, 取值0.1,0.2,0.3和0.4,序列中设置一个变点, 取值为0.5的情况下,在1000次模拟实验中,正确检测出变点的次数,变点的位置,以及每一次检测到变点之间的标准差和均方误差。从表中可以看出,随着样本量和长记忆参数 的增大(即序列越来越趋向于不平稳),与原方法相比较,新方法正确检测到变点的次数要多于原方法,且在检测到变点的位置上,总体上也更加准确。这些都可以从表中标准差,以及均方误差的数值差异中更加确切的体会到,总体上可以说明所提新方法的有效性。
Table 2. Correctly detect the number, position and error of one change point
表2. 正确检测出一个变点的次数,位置及误差
Table 3. Correctly detect the number, position and error of two change points
表3. 正确检测出两个变点的次数,位置及误差
表3给出了原方法与新方法在样本量分别为600,800和1000, 取值0.1,0.2,0.3和0.4,设置两个变点, 取值为0.5和0.75的情况下,在1000次模拟实验中,正确检测出变点的次数,变点的位置,以及每一次检测到变点之间的标准差和均方误差。从表中可以看出,随着样本量和长记忆参数 的增大(即序列越来越趋向于不平稳),与原方法相比较,新方法正确检测到变点的次数要多于原方法,且在每一次检测到变点的位置上,变点位置的标准差以及均方误差总体上较原方法更小,所以新方法较原方法对于长记忆时间多变点的检测更加准确,更加有效。
5. 实例分析
本节将采用一组实际数据来说明所提新方法的有效性,由于股票数据具有长记忆性,因此,选择上证指数1992年1月2日到2000年12月29日12年共2483个股票收益的数据,拿到数据后,先对数据进行对数处理,得到收益率的数据,经过取对数处理的数据图可以参见图1。用原似然比扫描方法对这组数据进行变点检测,结果检测出该组数据分别在第350,618,1116,1713,2081和2294这6个样本点存在变点,同样的,使用经过改良后的似然比扫描方法,重新对改组序列进行变点检测,检测结果显示在第228,1116,1605和1713这4个样本点的位置上存在变点。从图1中清晰的看到,在样本点1713之后检测出没有变点的结果更加符合具体情况,这说明原似然比扫描方法可能具有过估计的问题,而提出的新方法在检验长记忆时间序列均值变点上更加有效,更具有实用性和可靠性。
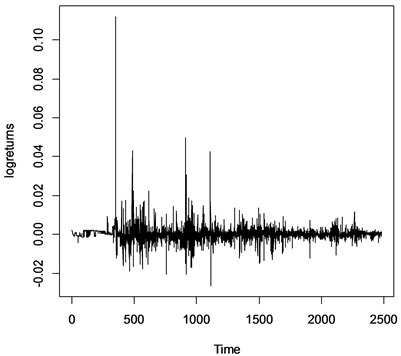
Figure 1. Yield of Shanghai composite index on January 2, 1992 solstice on December 29, 2000
图1. 上证指数1992年1月2日至2000年12月29日收益率
6. 小结
本文在似然比扫描方法的基础上,研究了新似然比扫描方法,用以检测具有长记忆性且带有均值多变点的时间序列,从模拟实验看,提出的新方法相较于原方法来说,实验结果更加理想,从实际数据的分析来看,相较于原方法,提出的新方法的检测结果更加符合实际情况,从而说明了新方法的有效性。
基金项目
国家自然科学基金(11661067);青海省自然科学基金(2019-ZJ-920)。
文章引用
徐琼瑶,邢玉红. 似然比扫描法在长记忆时间序列均值多变点中的应用
Application of Likelihood Ratio Scanning Method in Multiple Mean Changes in Long Memory Time Series[J]. 数据挖掘, 2019, 09(02): 9-17. https://doi.org/10.12677/HJDM.2019.92002
参考文献
- 1. Page, E.S. (1955) A Test for a Change in a Parameter Occurring at an Unknown Point. Biometrika, 42, 523-527. https://doi.org/10.1093/biomet/42.3-4.523
- 2. 王欣, 尹留志, 方兆本. 异常交易行为的甄别研究[J]. 数理统计与管理, 2009, 28(4): 671-677.
- 3. 张丕远, 王铮, 刘啸雷. 中国近2000年气候演变的阶段性[J]. 中国科学(B), 1994, 24(9): 998-1008.
- 4. Staudacher, M., Telser, S., Amann, A., Hinterhuber, H. and Ritsch-Marte, M. (2005) A New Method for Change Point Detection Developed for On-Line Analysis of the Heart Beat Variability during Sleep. Physica A, 349, 582-596. https://doi.org/10.1016/j.physa.2004.10.026
- 5. Kokoszka, P. and Leipus, R. (2000) Change-Point Estimation in ARCH Models. Bernoulli, 6, 513-539. https://doi.org/10.2307/3318673
- 6. Kokoszka, P. and Leipus, R. (1998) Change-Point in the Mean of Dependent Observations. Statistics & Probability Letters, 40, 385-393. https://doi.org/10.1016/S0167-7152(98)00145-X
- 7. Kokoszka, P. and Leipus, R. (1999) Testing for Parameter Changes in ARCH Model. Lithuanian Mathematical Journal, 39, 182-195. https://doi.org/10.1007/BF02469283
- 8. Kim, S., Cho, S. and Lee, S. (2000) On the CUSUM Test for Parameter Changes in GARCH(1,1) Models. Communication in Statistics-Theory and Methods, 29,445-462. https://doi.org/10.1080/03610920008832494
- 9. Lee, S., Tokutsu, Y. and Maekawa, K. (2004) The CUSUM Test for Parameter Change in Regression Models with ARCH Error. Journal of the Japanese Statistical Society, 34, 173-188. https://doi.org/10.14490/jjss.34.173
- 10. 马健琦, 陈占寿, 吕娜. 基于Sieve Bootstrap 方法的长记忆过程均值变点的检验[J]. 青海师范大学学报(自科版),2017, 33(2): 34-38.
- 11. 秦瑞兵, 田铮, 陈占寿. 独立随机序列均值多变点的非参数检验[J]. 应用概率统计, 2013, 29(5): 449-457.
- 12. Chen, Z., Tian, Z., et al. (2012) Moving Ratio Test for Multiple Changes in Persistence. Journal of Systems Science & Complexity, 25, 582-593. https://doi.org/10.1007/s11424-012-9255-9
- 13. Chen, Z., Jin, Z., Tian, Z., et al. (2012) Bootstrap Testing Multiple Changes in Persistence for a Heavy-Tailed Sequence. Computational Statistics & Data Analysis, 56, 2303-2316. https://doi.org/10.1016/j.csda.2012.01.011
- 14. Yao, Y.C. (1987) Approximating the Distribution of the Maximum Likelihood Estimate of the Change-Point in a Sequence of Independent Random Variables. The Annals of Statistics, 15, 1321-1328. https://doi.org/10.1214/aos/1176350509
- 15. Lavielle, M. and Ludena, C. (2000) The Multiple Change Points Problem for the Spectral Distribution. Bernoulii, 6, 845-869. https://doi.org/10.2307/3318759
- 16. Davis, R.A., Lee, T.C.M. and Rodriguez-Yam, G.A. (2006) Structural Break Estimation for Non-Stationary Time Series Models. Journal of the American Statistical Association, 101, 223-239. https://doi.org/10.1198/016214505000000745
- 17. Killick, R., Fearnhead, P. and Eckley, I.A. (2012) Optimal Detection of Change Points with a Linear Computational Cost. Journal of the American Statistical Association, 107, 1590-1598. https://doi.org/10.1080/01621459.2012.737745
- 18. Vostrikova, L. (1981) Detecting Disorder in Multidimensional Random Processes. Soviet Mathematics, Doklady, 24, 55-59.
- 19. Bai, J. (1997) Estimating Multiple Breaks One at a Time. Econometric Theory, 13, 315-352. https://doi.org/10.1017/S0266466600005831
- 20. Inclan, C. and Tiao, G.C. (1994) Use of Cumulative Sums of Squares for Retrospective Detection of Change of Variance. Journal of the American Statistical Association, 89, 913-923.
- 21. Berkes, J., Gombay, E. and Horvath, L. (2009) Testing for Changes in the Covariance Structure of Linear Processes. Journal of Statistical Planning and Inference, 139, 2044-2063. https://doi.org/10.1016/j.jspi.2008.09.004
- 22. Fryzlewicz, P. (2014) Wild Binary Segmentation for Multiple Change-Point Detection. The Annals of Statistics, 42, 2243-2281. https://doi.org/10.1214/14-AOS1245
- 23. Yau, C.Y. and Zhao, Z. (2016). Inference for Multiple Change Points in Time Series via Likelihood Ratio Scan Statistics. Journal of the Royal Statistical Society: Series B, 78, 895-916. https://doi.org/10.1111/rssb.12139
