Hans Journal of Data Mining
Vol.
10
No.
01
(
2020
), Article ID:
33406
,
15
pages
10.12677/HJDM.2020.101001
Semi-Structured Entity Resolution Algorithm
Hailang Wei, Gui Li, Zhengyu Li, Ziyang Han, Keyan Cao
School of Information and Control Engineering, Shenyang Jianzhu University, Shenyang Liaoning
Received: Nov. 21st, 2019; accepted: Dec. 4th, 2019; published: Dec. 11th, 2019

ABSTRACT
Entity resolution is the identification of similar or identical records in one or more datasets. In this paper, an entity resolution algorithm based on string similarity is proposed for semi-structured data with unknown patterns. The records are divided into several substrings, and the correlation between substrings is calculated by editing similarity. On this basis, the maximum weighted matching algorithm of binary graph is introduced to measure the correlation between records. Due to the computing time complexity of this method is higher, for Web entity resolution large data sets, the time cost is larger; therefore, this article also puts forward a kind of entity resolution algorithm based on set similarity, considering record as a collection of all the property values, each attribute value as the elements in the collection, using an array of tag to represent each element, according to these tags array for each record to create a signature, to find other similar records match the signature. The optimized maximum matching algorithm is used to select the truly similar records. Finally, this paper uses the actual data set to verify that the above method is more effective than the traditional method.
Keywords:Entity Resolution, Edit Similarity, Set Similarity, Maximum Weighted Matching of Binary Graph
半结构化实体解析算法
韦海浪,李贵,李征宇,韩子扬,曹科研
沈阳建筑大学信息与控制工程学院,辽宁 沈阳
收稿日期:2019年11月21日;录用日期:2019年12月4日;发布日期:2019年12月11日

摘 要
实体解析是指识别一个或多个数据集中的相似或相同的记录。该文主要针对模式未知的半结构化数据,提出了一种基于字符串相似度的实体解析算法,将记录分成多个子字符串,采用编辑相似度计算子字符串之间关联度,在此基础上引入二分图最大加权匹配算法度量记录之间的关联度。由于该方法的计算时间复杂度比较高,对于Web大数据集实体解析来说,所需的时间成本较大,因此,该文还提出了一种基于集合相似度的实体解析算法,将记录看作所有属性值的集合,每个属性值作为集合中的元素,用一个标记数组来表示每个元素,根据这些标记数组为每个记录创建一个签名,找出与签名相匹配的其他相似记录。并且采用优化后的最大匹配算法来选出真正相似的记录。最后,该文采用实际数据集进行实验验证了上述方法比传统方法更有效。
关键词 :实体解析,编辑相似度,集合相似度,二分图最大加权匹配

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着互联网技术的发展和应用,数据量越来越大,越来越多的数据分析师需要将不同Web数据源中指向现实世界同一实体的记录识别出来。然而这些数据往往是以模式未知的半结构化数据形式存储的。这些数据虽然存在一定的结构,但是结构不完全一致,往往存在着数据位移,属性缺失、属性值交错存储等问题,因此对数据集成造成了很大的困难。如表1所示的模式未知的两条记录,没有一个属性是完全匹配的,但实际上指的是同一个实体。
Table 1. Training data set
表1. 训练数据集
为了解决这个问题。本文提出下面的方法。首先,引入并改进了基于字符串相似度识别相似记录的算法。将每个记录的所有属性值作为一个长字符串,采用分隔符分词的方法将字符串分为多个子字符串,再对每个子字符串进行相似度计算,利用二分图最大加权匹配 [1] 算法计算出相似记录。由于在Web大数据集中该算法的最坏的运行时间复杂度是O(n3m2),其中n是子字符串的数量,m是记录的数量 [1]。因此,本文还引入并改进了基于集合相关性识别相关记录的算法来降低m的数量。将记录看作所有属性值的集合,每个属性值作为集合中的元素,用一个标记数组来表示每个元素,根据这些标记数组为每个记录创建一个签名,找出与签名相匹配的其他相似记录。最后采用基于三角不等式优化了的最大二分图匹配的方法来选出真正相似的记录。这里将两个集合作为二分图的两边(每个元素假设为一个顶点),用相似性函数来测量元素之间的相似度。
本文的主要贡献如下:
1) 提出一种不考虑模式、类型的记录相似度定义,能够有效的表达半结构化记录的相似性。
2) 在本文定义的字符串相似度基础上,引入最大二分图加权匹配算法(Kuhn-Munkres算法)有效计算记录之间的相关性。
3) 为了减少候选记录之间的比较次数,引入并改进集合相似性,为记录创建有效签名空间,以及生成最优签名的步骤,将签名和倒排索引结合,对相关记录进行初步选择。
4) 为了降低最大匹配算法的时间复杂度,采用两种新的过滤器,减少不相关的候选集,同时采用三角不等式来优化最大匹配方法。
论文的其余章节组织如下。本文在第2节介绍了目前阶段对于半结构化实体解析的一些相关工作,第3节介绍了集合相关性和字符串相似度的相关理论,在第4节和第5节给出了基于字符串相似度和集合相似度识别相关记录的模型,提出相应的算法,最后在第6节对算法进行实验验证。第7节进行了总结。
2. 相关工作
实体解析又被称为记录链接、对象识别、重复检测等。经过近几年的发展,有一系列实体解析技术问世;文献 [2] 是对早期实体解析工作的综述;文献 [3] [4] [5] 是国内对实体解析技术的研究综述;文献 [6] 用记录的相关字段构成键,按照键对记录进行排序,然后按顺序对记录进行相似度检测。文献 [7] 把每条记录看成字符串,对记录进行排序,然后使用固定大小的优先队列按顺序扫描已排序的记录,并将它们聚类;文献 [8] 采用N-gram方法对记录进行聚类;文献 [9] 将每个字段值分解成多个tokens,对tokens进行排序,进而对记录进行排序,使用滑动窗口的方法来比较临近范围的记录。文献 [10] 提出了一个近似的Jaccard相似性度量来评估两个字符串之间的相似性。文献 [1] [11] 提出了用于集合相似性搜索和连接的近似算法。文献 [12] 提出了使用前缀过滤器来解决集合相似性连接问题。这些工作都未考虑到这种模式未知的半结构化数据,不适用于处理Web数据源大数据集中的实体解析。
3. 相关理论
3.1. 字符串相似度
本文将每条记录的所有属性值作为一个长字符串,用标点符号作为分隔符分词法将字符串分为多个子字符串,这些子字符串之间的相关性用编辑相似度计算。编辑相似度公式为:
其中 和 为x和y的长度。 表示字符串x和y之间的编辑距离(Edit Distance)。字符串编辑距离是建立在一系列编辑操作(字符串中单个字符的插入、删除和替换)的基础之上的,通常每个编辑操作会被分配一个代价来表示其发生的可能性。给定一个编辑操作的集合和它们的代价,两个字符串x和y之间的编辑距离 被定义为:把字符串x转换成字符串y所需要采取的编辑操作序列的最小代价。下面给出编辑操作,编辑操作的代价和编辑距离的形式化定义:
定义1:令A是字符的有限集合,A*是A上所有串的集合, 表示空字符, , 表示字符串x的长度。
编辑操作指:
替换: (如果a = b,则被称为一致替换,否则为非一致替换);
删除: ;
插入: ;
定义2:代价函数指的是每个编辑操作指定一个[0,1]之间的非负实数为代价的函数。令 , 和 ,分别表示替换,删除和插入操作的代价,对于一个编辑操作的序列 ,其代价被定义为公式:
其中规定任何一致替换的代价都是0。
定义3:两个字符串x和y之间的编辑距离 被定义为:把字符串x转换成字符串y所需要采取的编辑操作序列的最小代价。即:
在确定这些子字符串之间的相似度后,为了描述记录之间的相关性,结合上述子字符串之间的编辑相似度,引入了第4.2节中的二分图最大加权匹配算法 [1],求出记录之间的最大加权匹配分数作为记录之间的相似度 。
3.2. 集合相关性
首先将两个集合R和S的相关性概念形式化。在这里主要采用的是Jaccard相似度函数来识别相似度较高的元素对。假设用相似度函数 来表示两个元素x和y之间的Jaccard相似度,取值范围在[0,1]之间,1代表完全相似,0代表完全不同。为此提供了相似度阈值 ,相似函数 的定义如下:
从上述定义中可以看出,相似度大于或等于阈值 的元素视为匹配元素。
给出一个相似函数 为两个集合R和S构建加权二分图。图中每个顶点代表R或S中的元素,使用 为连接顶点的边加权。然后求出该图的最大加权二分图匹配 [1],其中一个数据集中的每个顶点恰好与另一个数据集中的一个顶点相连接,使边的权值之和达到最大值。最大匹配的分数就是边权重之和。本文用 [13] [14] 表示最大匹配分数。定义4给出了基于最大匹配分数的集合相关性定义:
定义4:假设两个集合R和S中含有相似的元素则称两个集合相关,用 来表示,相似函数为 。将集合相关性分为下面两种情况:
1) SET-SIMILARITY:检查两个集合是否相似。则SET-SIMILARITY计算公式为:
2) SET-CONTAINMENT:检查一个集合是否是另一个集合的子集。其中 ,则SET-CONTAINMENT的计算公式为:
根据用户需求取阈值 ,当且仅当 时,两个集合就被称为相关的。
4. 基于字符串相似度的实体解析算法
4.1. 数据分词
由于半结构化数据常常表现为模式未知或属性值为文本型字符串的形式存储(表1),很难直接判断出记录之间的关联性。因此首先指定以下分词规则对数据进行处理:
将半结构化数据集中的每条记录的所有属性值作为一个长字符串(如表2),并采用分隔符将每个记录分隔成多个子字符串。例如将表2中数据采用顿号分隔符分为表3的多个子字符串。
Table 2. Training data set string representation
表2. 训练数据集字符串表示
Table 3. Data segmentation results
表3. 数据分词结果
4.2. 记录相关性计算
为了衡量记录之间的相关性,首先结合4.1节中的分词结果,计算出这些子字符串之间的编辑相似度。根据基于子字符串的相似度来定义记录的相似度。提出了一种基于二分图最优匹配的相似度定义,方法如下:
根据待比较的两条记录ri和rj生成一个完全有权二分图 ,其中V1中每个节点u代表ri的一个子字符串ui,V2中的每个节点v代表rj的一个子字符串vj, ,权函数W定义为3.1节中两个子字符串之间的相似度 。 是B的最优匹配,其中 ,
。则记录ri和rj的相似度定义为: 其中m、n分别代表ri和rj的子字符串个数。
本文采用Kuhn-Munkres算法(KM算法)来计算记录的相似度,下面给出具体的算法流程:
1) 由算法1构造两条记录的完全二分图;
2) 算法2计算两条记录相似性,其中 返回r1的第i个字符串和r2的第j个字符串之间的相似性, 指的是二分图的最优匹配,返回最优匹配中所有权值之和,其中B表示完全二分图,w是B的权值矩阵,m是w的阶;
3) 根据用户需求给定阈值 ,用算法3将记录之间相似度大于该阈值的记录选择出来作为相似记录对。
5. 基于集合相关性的实体解析算法
第4节描述的方法虽然能快速的找到相似记录,但是其算法时间复杂度为O(n3m2),其中n是子字符串的数量,m是记录的数量。本节在第4节算法的基础上进行了改进,减少m的数量。
5.1. 属性值规范化标记分词及创建倒排索引表
首先将这些字段分为字符型和数值型并对其标记化分词处理:
数值型字段:例如表示地图坐标的字段(121.575509, 38.945373)由于不同数据源中表示的方式不同,在这里,统一将数值型字段精确到小数点后两位。
字符型字段:采用基于领域词典(基于城市,地区等划分的词典)的分词法,例如将“东至规划路”和“东规划路”统一规范化为“规划路”。
Table 4. Semi-structured tag array collection representation
表4. 半结构化标记数组集合表示
表4中,R是一个参考集,对应于一个实体记录,S是用于搜索相关集合的记录集合。将表1中的记录划分为表4中记录R的12个字段,在这里用符号ti代替标记,按照这些分词频率递减的顺序作为标记化后的下标。此外将记录中的每个文本属性都看作一个元素。每个元素都用一组标记(例如 ,t1 = 西南路,t5 = AB区,t6 = 沙河口区,t4 = 春风街,t7 = 1号,t8 = 905-1号)来表示。对于S数据集,使用上述生成的标记为该数据集按照标记在各个元素中出现的频率创建一个倒排索引表。
5.2. 有效签名生成
本节将签名和倒排索引一起使用来识别相关的集合对。该算法从5.1节中生成的标记集合中找到一个子集来生成一个有效签名。通过这个签名来寻找相关的候选集,从而删除不相关的候选集。
5.2.1. 有效签名
在集合R中,假设每个元素 都是一个标记数组。则定义所有标记的集合为 。根据标记集合,定义一个签名如下:
定义5 (签名):给定一个集合R,则标记集合 的任何子集都是R的签名。
定义6 (有效签名):给定一个集合R和一个相关性阈值 ,如果任何可能匹配的集合S满足 ,同时在 中有一个签名 ,使 ,那么该签名 为有效签名。
如果给定集合 的一个签名 ,那么将有效签名定义为 ,其中 (即, 是 的一组签名标记)。
例1:对于表4中的集合R,有 ,假设子集 是集合R的一个可能的签名。相应的有效签名就是 。
5.2.2. 加权签名方案
最大匹配阈值:在处理签名时,定义一个相关量θ,作为最大匹配阈值。最大匹配阈值是基于 和 定义的。
对于 ,要判断R和S的关联性则需要满足:
即 。因此本文为 定义了最大匹配阈值 。
对于 要想判断R与S相关联则需要满足公式:
鉴于 ,则有:
所以对于 来说最大匹配分数也是 。
加权签名方案:加权签名方案是在未加权签名方案 [13] 中的所有签名基础上,为集合创建一个相似度上限更严格的签名。下面给出该签名方案的方法:
给出r中任何元素与s之间的jaccard相似度计算公式为: ,对于任何元素r,假设有一个元素s只与r共享一个标记;它会有一个相似的分数 。那么当一个元素s与r共享x个标记时,其相似度得分为: 。这个上界 为r中的每个标记赋予权值 ,表示每个标记对总体最大匹配得分的贡献的上限。
下面形式化定义了加权签名方案。
定义7 (加权签名方案)给定一个集合 和一个关联阈值 ,加权签名方案是所有含有满足 的有效签名集合 的总和签名 。
例3:以表4中的集合R为例,假设 。拐点 。 在加权签名方案中是图1中的一个有效签名 的有效签名,其中
。
5.2.3. 最优签名选择
在上文中,选择倒排索引表中集合的并集作为相关候选集。因此,如何最大限度减少这个并集的规模,选择最优签名是一个主要问题。在本文中,采用与该并集大小成正比的倒排索引表的总长度作为优化目标。
问题(最优有效签名选择):给定一个集合R和一个关联阈值 ,找到一个有效签名 满足可以使
最小化, 指的是倒排索引表中标记的个数。
本文中,将这个问题看做是一个背包问题,使用贪心近似算法来解决。下面给出该方法步骤:
1) 给出一个集合 ,对于每一个在 中的t,给它赋值 以及一个代价 ;
2) 为了最小化倒排序列的大小,在 中按cost/value对所有标记以递增次序进行排序;
3) 依次选择标记,直到定义7中的条件得到满足为止,得到有效签名,其中所选的标记是 的签名标记;
例4:考虑表4,图2中表示了这个倒排索引,costs (即:索引列表的长度)为在 中的12个tokens 分别为9,7,7,6,6,6,5,3,3,1,1,1。Values对于 值为8/15, 的值为1/3每个
值为11/30, 为1/6, 为1/5。我们可以基于cost/value值按照递增序列排序并对他们进行选择。首先选 , 以及 。因此,有 比值 大。然后继续选择 ;如果选择 ,就有 以及 。则有 ,比 小,停止继续选择,则有效签名为 。
5.3. 候选集过滤
尽管上述方法删除了许多不相关的集合,但仍然会产生许多不相关的候选集。为了进一步删除误报的候选集,采用检查过滤器和最近邻过滤器来删除误报候选集。
5.3.1. 检查过滤器
通过上述有效签名的创建,已经确定了与ki共享标记的元素s,那么可以近似的计算出 。如果证明所有r中的共享标记ki和s仍然满足 ,那么集合S将作为候选集(即使S与 只共享一个标记)。该方法被称为检查过滤器。
算法4描述了检查过滤器。对签名中的每一个标记,检索与签名匹配的倒排索引列表。如果集合通过5~6行中的步骤,则将集合添加到候选集合中。
例5:以表4为例。假设 ,有含 的有效签名集合 。访问相应的倒排列表,并在三个候选集S2、S3和S4上测试检查过滤器。S2没有通过检查过滤器 , 。S3和S4通过检查过滤器 和 。
5.3.2. 最近邻过滤器
最近邻过滤器,即R和S之间的最大匹配分数值不会超过R中每个元素与其在S中最相似的元素(最近邻)的相似性总和:
所以,如果有一个候选集S的最近邻相似度之和小于θ,那么就可以删除这个候选集。本文采用下面几种技术来优化该过滤器。
1) 搜索有效最近邻:遍历每个标记 ,对于每一个标记t,使用倒排索引表I[t]获取S中包含标记t的所有元素s。计算得到r和每个s之间的相似性;相似度得分最大的s被认为是最近邻。
2) 计算重用:在检查过滤器中,已经计算了r和 中包含r的签名标记的所有元素之间的实际相
似度。由于这些超过 的最大值之外的的其他不包含r签名标记的元素其相似度分数一定不会超过 界限,所以这个相似度最大值一定是最近邻相似度。
3) 提前终止:对于 中签名标记出现在候选集合S中的元素,其最近邻相似度并不能保证
,因此要么重用检查过滤器中的计算公式,要么直接进行最近邻搜索。而对于签名标记没有出现在S集合中的元素 ,对所有 边界 仍然保留。该算法首先通过对匹配元素r的最近邻相似性进行求和来推断出一个总的估计值,并使用 估计非匹配元素 。然后,遍历每个 ,使用 的最近邻相似性来更新总估计值。如果总估计低于θ,则删除该候选集。
算法5描述了最近邻过滤器。NNSearch指最近邻搜索步骤。在第3步构建一个总估计值,4~5行计算匹配元素的最近邻相似度,6~9行计算不匹配元素的最近邻相似度与提前终止的最近邻相似度。
例6:以表4为例,假设 。对于候选集S3。当 和 共享签名标记。 的最近邻是 ,他们
的相似分数为5/6。对于 ,给它一个相似分数上界 。对于 ,尽管 与签名 相似,但是它没有通过检查过滤器,因此也可以给它一个上界 。然后为 做最近邻搜索,发现 的相似度为0.25。因此 的相似度分数上界更新为0.25。则总估计值为 ,因此提前
终止最近的邻居过滤器并删除候选集S3。
5.4. 最大匹配验证
在本节中,将对最大匹配验证进行优化。假设 为相似函数 的对偶距离函数。可以看出,如果距离函数满足一定的约束条件(例如:满足三角不等式),则最大匹配中一定存在相同的元素。假设有一对相同的元素r和s与其他元素 和 的关系有:
(1)
(2)
(3)
(4)
(5)
在(1)中,将相似函数转换为它们的对偶距离函数。在(2)中使用r = s,并在(3)中应用三角形不等式,从(4)到(5),由于r = s则使用 来替换,在(5)中,可以看出连接r和s比连接r到 和 到s更好。因此,r和s一定存在于最大匹配中。
应用这个三角不等式,本文从R和S中移除了所有相同的元素,并且在生成的集合上应用最大匹配算法。在最大匹配之后,将相同元素的数量添加到最大匹配分数中,即为最终的最大匹配分数,如表4中的数据,经验证S4即为与R相关的记录。
6. 实验评估
6.1. 数据集
本文用Python对“面向领域的Web数据抽取”项目所抽取的多个数据源的房地产数据进行实验。抽取到的数据信息量如下表5。这些数据记录都是以模式未知的半结构化数据存储的。可能存在的记录之间的差异有:数据物理存储顺序差异,数据丢失,数据类型差异以及属性交叉存储等。
Table 5. Statistics of information extracted from real estate
表5. 房地产抽取信息量统计
6.2. 实验方法
本文采用三种实体解析方法进行实验(表6)。
Table 6. Description of experimental methods
表6. 实验方法描述
6.3. 实验结果及分析
为了使实验更具说服力本文分别从抽取到的房地产数据中随机抽取500,000条数据进行实验,其中有1000条重复数据。根据用户需求取记录相似度阈值 分别为0.70,0.75,0.80。来对上述三种方法进行实验分析。
评价指标:本文采用精确度(precision)、召回率(recall)、F1-score,对实验结果进行评估分析。精确度(P)是分块正确的正例数量占所有分为正例的百分比,召回率(R)是分块正确的正例数量占实际正例数量的百分比,F1-score是它们的调和均值。同时采用运行时间来比较三种方法的运行速率。
从图1中可以看出,本文提出的两种模式未知的实体解析算法与传统的实体解析算法相比在精确率、召回率以及F1-score上几乎相同,甚至能优于传统的方法。从图2中可以看出,本文提出的两种算法比传统的方法在运行速率上能提高不少。而基于集合相似度的算法更优于基于字符串相似度的算法。从图3中,比较了采用三种方法最终选择出的候选集个数,通过该表可以明显的看出基于集合相似性的方法大大减少了候选集m的个数。通过实验结果,可以看出本文提出的两种方法,在保证了与传统算法相同的结果的同时,提高了算法的运行速率,解决了模式未知的半结构化数据集实体解析的问题。
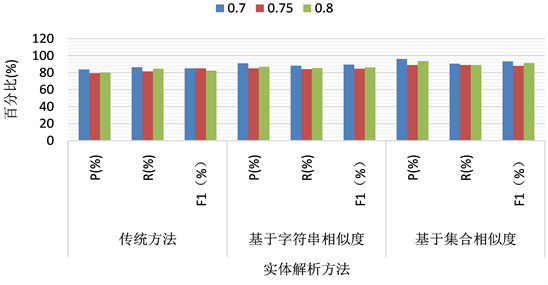
Figure 1. Experimental results of the three methods
图1. 三种方法的实验结果

Figure 2. Running time comparison of three methods under different thresholds
图2. 三种方法在不同阈值下的运行时间比较

Figure 3. Comparison of the number of candidate sets of the three methods
图3. 三种方法候选集个数的比较
7. 总结
本文研究了模式未知的半结构化数据实体解析问题,提出了一种基于字符串相似度的二分图最大加权匹配计算模式未知的记录相似度的方法,在此基础上,又提出了一种基于集合相似性的改进了的二分图最大加权匹配方法来解决实体解析问题。最后通过实验验证了在保证与传统方法实验结果相同的情况下,这两种方法提高了运行速率。理论分析和实验结果表明,这两种方法是正确且有效的。
基金项目
国家自然科学基金(No.61602323);辽宁省博士启动基金(No.201601209);住建部科学技术项目(No. 2017-K8-038)。
文章引用
韦海浪,李 贵,李征宇,韩子扬,曹科研. 半结构化实体解析算法
Semi-Structured Entity Resolution Algorithm[J]. 数据挖掘, 2020, 10(01): 1-15. https://doi.org/10.12677/HJDM.2020.101001
参考文献
- 1. Galil, Z. (1986) Efficient Algorithms for Finding Maximum Matching in Graphs. ACM Computing Surveys, 18, 23-38.
https://doi.org/10.1145/6462.6502 - 2. Elmagarmid, A.K. and Member, S. (2007) Duplicate Record Detection: A Survey. IEEE Transactions on Knowledge and Data Engineering, 19, 1-16.
https://doi.org/10.1109/TKDE.2007.250581 - 3. 高广尚. 面向实体解析的无监督聚类方法综述[J]. 计算机工程与应用, 2018(7): 11-19.
- 4. 高广尚, 张智雄. 关于实体解析基本方法的研究和述评[J]. 数据分析与知识发现, 2019, 3(5): 27-40.
- 5. 王宁, 李杰. 大数据环境下用于实体解析的两层相关性聚类方法[J]. 计算机研究与发展, 2014, 51(9): 2108-2116.
- 6. Hernandez, M. and Stolfo, S. (1995) The Merge Purge Problem for Large Databases. ACM, New York.
https://doi.org/10.1145/223784.223807 - 7. Monge, A.E. and Elkan, C.E. (1997) An Efficient Do-main-Independent Algorithm for Detecting Approximately Duplicate Database Records. Proceedings of Workshop on Research Issues on Data Mining and Knowledge Discovery, Newport Beach, 14-17 August 1997, 23-29.
- 8. Gravano, L. and Ipeirotis, P.G. (2001) Using Q-Grams in a DBMS for Approximate String Processing. IEEE Data Engineering Bulletin, 24, 28-34.
- 9. Ristad, E.S. and Yianilos, P.N. (1998) Learning String-Edit Distance. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20, 522-532.
https://doi.org/10.1109/34.682181 - 10. Deng, D., Fer-nandez, R.C., Abedjan, Z., Wang, S., Stonebraker, M., Elmagarmid, A., Ilyas, I.F., Madden, S., Ouzzani, M. and Tang, N. (2017) The Data Civilizer System. 8th Biennial Conference on Innovative Data Systems Research, Chaminade, CA, USA, 8-11 January 2017, 7 p.
- 11. Deng, D., Li, G. and Feng, J. (2014) A Pivotal Prefix Based Filtering Algorithm for String Similarity Search. ACM SIGMOD International Conference on Management of Data, Snowbird, 22-27 June 2014, 673-684.
https://doi.org/10.1145/2588555.2593675 - 12. Fredman, M.L. and Tarjan, R.E. (1987) Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms. Journal of the ACM, 34, 596-615.
https://doi.org/10.1145/28869.28874 - 13. Wang, J., Li, G. and Feng, J. (2011) Fast-Join: An Efficient Method for Fuzzy Token Matching Based String Similarity Join. 27th International Conference on Data Engineering, 11-16 April 2011, 458-469.
https://doi.org/10.1109/ICDE.2011.5767865 - 14. Wang, J., Li, G. and Feng, J. (2014) Extending String Similarity Join to Tolerant Fuzzy Token Matching. ACM Transactions on Database Systems, 39, 7.
https://doi.org/10.1145/2535628
