Advances in Porous Flow
Vol.4 No.01(2014), Article ID:13252,8 pages
DOI:10.12677/APF.2014.41001
Experimental Study and Mathematical Model on Permeability of Clayey Soil with Shear Deformation
HydroChina Kunming Engineering Corporation, Kunming
Email: hongjunlei@126.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jan. 13th, 2014; revised: Feb. 10th, 2014; accepted: Feb. 20th, 2014
ABSTRACT
A new seepage device was developed to measure permeability of clayey soil under different physical and mechanical status with shearing deformations. A series of seepage tests were carried out on a certain clayey soil and indicated that permeability of the soil was related with many factors, among which the shearing strain and confining pressure were the most important. Based on the testing results and mechanism analysis, a new relation model of permeability to reflect effect of physical and mechanical status was raised. The model was then fitted and checked by the testing results.
Keywords:Permeability; Shearing Deformation; Seepage; Mathematical Model

粘性土剪切变形中渗透性试验
研究及数学模型
雷红军
中国水电顾问集团昆明勘测设计研究院,昆明
Email: hongjunlei@126.com
收稿日期:2014年1月13日;修回日期:2014年2月10日;录用日期:2014年2月20日

摘 要
本文研制了一种新型的渗流试验设备,用以测定土体在发生剪切变形过程中不同物理力学状态条件下的渗透系数,针对某种粘性土进行了一系列试验,结果表明粘性土剪切变形过程中的渗透系数受到多种因素的影响,其中剪切应变和围压的影响最为显著。在此基础上提出了一个可反映土体物理状态变化及剪切中结构变化对其渗透性影响的数学模型,通过试验数据拟合验证,结果表明该模型可有效反映土体剪切变形过程中不同物理力学状态条件下的渗透系数。
关键词
渗透系数;剪切变形;渗流;数学模型

1. 引言
渗透系数是土的最重要的参数之一,一般随物理力学状态的变化而变化。但由于问题的复杂性,在一般的岩土工程设计计算中,渗透系数通常被假设为常数,但这种假设有时可能给设计计算结果带来很大误差。因此有必要针对土体物理力学状态变化时的渗透性进行深入研究。
目前,有学者研究了土体渗透性与物理指标如初始孔隙率、饱和度、粒径级配等的关系。Chu等采用不同的试验方法测定了某粘性土的渗透性[1] ,结果表明渗透系数随深度增加而逐渐降低。Marshall通过试验研究了粘性土孔隙比对渗透性的影响[2] ,结果表明孔隙比对粘性土的渗透性有重要影响,同种粘性土的渗透性随孔隙比的减小而迅速减小。Nishida等针对大量粘性土的渗透性试验结果表明粘性土的渗透系数与其孔隙比有密切关系[3] 。Garcia对某淤泥质粘性土进行了试验研究[4] ,定性分析了孔隙分布对土体渗透系数的影响。Bryant对某工程场地的粘性土进行了渗透试验[4] ,研究了土体平均粒径和土体密度对其渗透性的影响。
也有一些学者研究了力学状态如围压、固结度等对渗透性的影响。Chan利用三轴仪对某粘性土进行了渗透试验[5] ,测定了垂直于层面及平行层面两个方向的渗透系数,求得了两个方向的渗透比率,但试验过程中没有改变试样的受力条件。Carpenter在三轴仪中对某粘性土进行了渗透试验[6] ,研究了试样尺寸、水力坡降、渗透历时以及渗流出口处的有效应力等因素对渗透系数的影响,得出了一些有益的结果,但试验中没有考虑应力状态变化对土体渗透性及渗透各向异性的影响。在国内,朱建华进行了某粘性土的室内渗透试验[7] ,分析了渗流出口处有效应力、试样长度、水力坡降及渗透历时对土体渗透系数的影响,认为粘性土渗透性受有效应力的影响较大,随有效应力的增加而降低。李平通过在三轴仪中对某饱和粘性土试样的渗透试验[8] ,研究了初始孔隙比、固结度、周围压力对土体渗透性的影响,结果表明对相同初始孔隙比的试样,固结后土体的渗透系数与孔隙比在半对数坐标系下呈近似直线关系,且土体渗透系数随固结度和周围压力的增大而减小。
实际上,土体常处于不等向应力的剪切过程中,因土体剪切引起的物理力学状态变化是引起其渗透性变化的根本原因。而目前的试验研究中,土体要么没有发生变形,要么只是发生等向固结变形,均没有考虑不等向剪切变形的影响。
本文研制了一种新型的试验设备,可测试粘性土发生不等向剪切变形时的渗透系数。通过一系列试验,分析了不等向剪切变形对土体渗透性的影响,基于试验成果,提出了一种粘性土渗透系数的数学模型,并通过实测数据对该模型进行了拟合验证。
2. 试验装置和试验土料
2.1. 试验装置
试验装置原理示意图如图1所示,是在三轴仪的基础上通过改进底座和上帽并增加内部三向渗透系统而得。试样为长方体形状,尺寸为长9 cm、宽4.5 cm、高11 cm。改造的底座与顶帽主体部分水平横断面均为椭圆形,与试样接触部位为方形,中间设置平滑过渡。试样放置在底座的方形平台上,上面放置顶帽。在底座和上帽中设置三向渗透管路及开关控制系统,以实现试样三个垂直方向上任一方向的渗流。
试样的固结和剪切功能通过三轴仪本身的围压和轴向剪切系统实现。当试样被剪切至某轴向变形时,通过控制渗流管路的开合,对试样某一方向两侧表面施加水压力,通过预先放置于试样渗透方向的两侧表面上的透水性土工织物实现导水渗流。试验过程中,试样的剪切过程需足够慢,以尽量减小剪切产生的超静孔隙水压力影响。
渗流试验中,当流量趋稳时,记录相应时刻试样的围压、轴向应力、轴向位移、渗流量及时间等,通过相应计算获得试样当前状态下的渗透系数。然后,试样可被继续剪切至不同轴向变形后再次进行渗流试验,如此反复多次可得到试样在不同剪切变形条件下的一系列渗透系数。
更换试样,可改变试样围压、渗透方向、渗透水压力等条件,研究试样的渗透性变化规律。
2.2. 试验土料
试验土料为某心墙堆石坝的心墙粘性土,主要的物理指标如表1所示,级配曲线如图2所示。
为了解试验土料的力学性质,首先进行了常规三轴试验,结果表明该土料的剪胀性很弱。

Figure 1. Sketch map of the seepage test device
1-底座;2-量水管;3-出水管与阀门;4-X方向渗流进水管;5-Y方向渗流进水管;6-Z方向渗流进水管;7-试样;8-进水侧土工织物;9-出水侧土工织物;10-上帽;11-X方向渗流出水管;12-Y方向渗流出水管;13-Z方向渗流出水管;14-传力杆
图1. 渗流试验装置示意图
表1. 试验土料的物理指标
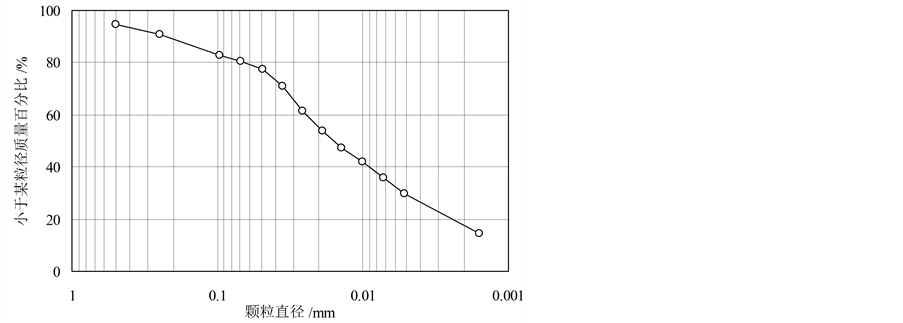
Figure 2. Gradation curve of the testing soil
图2. 试验土料的粒径级配曲线
3. 典型试验结果与分析
利用研制的试验装置,针对上述土料,分别在试样的三个垂直方向,进行了不同剪切应变、围压、渗透压力等条件下的渗透试验,求取了一系列的渗透系数,以下针对典型试验结果进行分析。
3.1. 不同剪切应变和围压条件下的渗透性
图3表示了试样在不同围压条件下发生不同的轴向剪切应变后的渗透系数,对应的渗透方向为Y方向,渗透水压力为50 kPa。从图3可以看出:
1) 在试样承受不等向应力发生剪切应变的起始阶段,渗透系数迅速减小,随着轴向应变的增加,变化速率越来越慢,最后渗透系数基本趋于稳定。
2) 低围压下,渗透系数变化幅度较大,最大可达数十倍,而高围压下渗透系数的变化幅度相对较小,一般只有3~5倍。
3) 在低围压如100 kPa、300 kPa时,试样在轴向应变增加到某一程度时,渗透系数有反向增加趋势,但增加幅度不明显。高围压下试样的渗透系数没有反向增加现象。
4) 不同围压下的试样在产生相同的轴向应变时,围压小的试样其渗透系数较大,围压大的试样其渗透系数较小。且这种差别随围压的增加而逐步变得不明显。
以上结果可解释如下:在轴向应变不大的起始阶段,试样在压缩及剪切作用下变得越来越密实,水流在试样中的通过变得越来越困难,渗透系数逐步减小。随着轴向位移的继续增加,土样密度的增加幅度越来越小,其渗透系数的变化也越来越慢。低围压下试样渗透系数反向增加的现象可能与试样的剪胀特性有关,由于试验土料的的剪胀性很弱,因此这种反向增加的现象及幅度也很弱,且随着围压的升高表现得越来越弱,直至消失。
3.2. 不同方向的渗透系数
图4表示在700 kPa围压下,针对三个试样,分别在X、Y、Z三个垂直方向施加50 kPa渗透压力时,
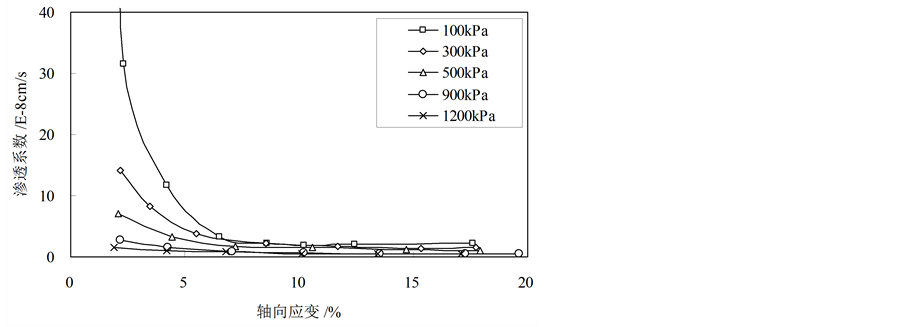
Figure 3. Permeability under different axial strain
图3. 试样渗透系数随轴向应变的变化
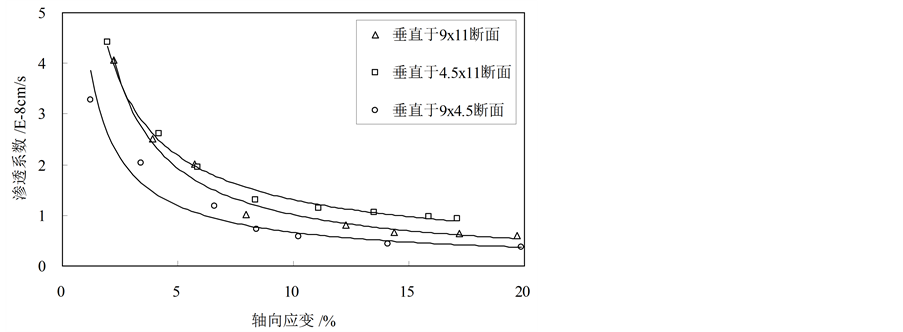
Figure 4. Permeability in different directions
图4. 不同方向的渗透系数
试样渗透系数随轴向应变的变化。
可以看出,三个方向渗透系数总体变化趋势均表现为逐步减小,与上述特点类似。但在与剪切方向相对关系不同的渗透方向上,渗透系数存在差异,竖直方向渗透系数小于水平方向,这可能与土体的各向异性有关。
4. 渗透性数学模型
4.1. 渗透系数与孔隙比的关系
计算出试样在不同轴向应变条件下的孔隙比,并将其与对应的渗透系数值绘制于半对数坐标系中,如图5所示。
可以看出,试样的渗透系数随孔隙比增加而增加。围压较低的试样,其孔隙比相对较大,而高围压试样的孔隙比相对较小,这是由于围压大小对试样等向固结和剪切过程中的排水量有较大影响。
在图5中,各围压对应的曲线的起始点在每一系列曲线中的孔隙比为最大,此时试样的轴向应变很小,其渗透系数接近于试样等向固结完毕而尚未发生不等向剪切变形时的渗透系数。因此,将这些曲线按变化趋势做反向延伸,估算得到各围压下试样仅发生等向固结时的渗透系数,得到点A、B、C、D、E如图5所示。可以看出,A、B、C、D、E五点基本在同一条直线上,这条直线可反映出试样只发生等向固结变形时的渗透系数与孔隙比的关系,称之为“等向固结渗透系数线”,即只发生等向固结的试样,其渗透系数沿“等向固结渗透系数线”的趋势变化。当试样发生不等向剪切变形时,其渗透系数值发生向下偏移并脱离“等向固结渗透系数线”,此时的渗透系数与试样的应力状态有关。
4.2. 渗透系数与剪应力水平的关系
在图5中,不同围压下的试样渗透系数变化趋势不同,表明渗透系数并不只取决于孔隙比,还与试样的应力状态有关。本文选取剪应力水平表示土体应力状态的变化,剪应力水平可反映土体剪切引起的结构变化,而研究表明,结构对于土体的渗透性有较大影响。剪应力水平是土体剪切破坏面上的剪应力与其抗剪强度的比值,可按下述公式计算。
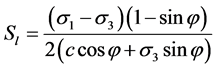 (1)
(1)
其中,σ1、σ3、c、φ分别是大主应力、小主应力、粘聚力和内摩擦角。
计算出试样在不同轴向应变下的剪应力水平,将其与对应的渗透系数绘制于半对数坐标系中如图6所示。可以看出,试样的渗透系数随剪应力水平的增加而逐步降低。当剪应力水平较小时,渗透系数的变化速率较快,剪应力水平较高时,渗透系数的变化速率减慢。同一围压条件下,对应于不同的剪应力

Figure 5. Permeability and void ratio in semi-log coordinate system
图5. 半对数坐标系中渗透系数与孔隙比的关系
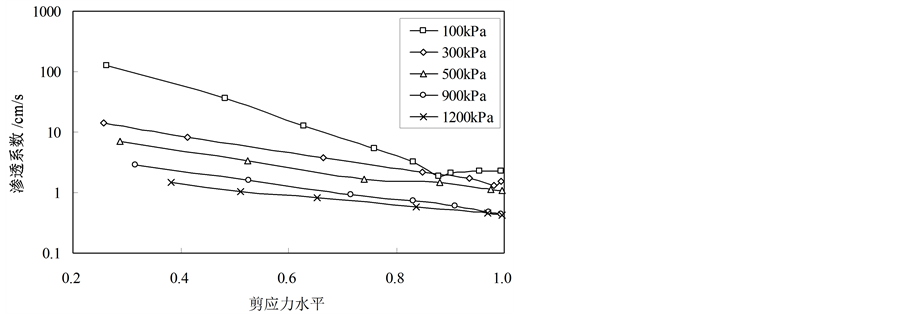
Figure 6. Permeability and shearing stress level in semi-log coordinate system
图6. 半对数坐标系中渗透系数与剪应力水平的关系
水平,试样的渗透系数不同,表明剪应力水平也是影响土体渗透系数的重要因素。
4.3. 土体剪切变形中渗透系数数学模型
本文建议用式(2)所示指数函数描述粘性土剪切变形中渗透系数与孔隙比和剪应力水平的关系。
 (2)
(2)
其中,k、e、Sl分别是渗透系数、孔隙率和剪应力水平,a、b、c是模型参数,可通过一组试验求取。
式(2)可转化为式(3)。
 (3)
(3)
在式(3)中,第一部分 可反映土体物理状态变化对渗透系数的影响,第二部分
可反映土体物理状态变化对渗透系数的影响,第二部分 则从力学状态的角度反映了土体剪切作用引起的结构变化对渗透系数的影响。
则从力学状态的角度反映了土体剪切作用引起的结构变化对渗透系数的影响。
当剪应力水平Sl = 0,即土体只发生等向固结变形时,式(3)退化为
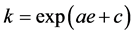 (4)
(4)
式(4)即前文所述的“等向固结渗透系数线”。
4.4. 数学模型的空间形式
式(2)可以表示为一个空间曲面如图7所示,其中两个水平向坐标轴分别为孔隙比e和剪应力水平Sl,竖直向坐标轴为渗透系数k。这个空间曲面上的任意一点均对应于一个具有一定孔隙比和剪应力水平的土体的渗透系数值。
当试样只发生等向固结时,剪应力水平Sl为0并保持不变,此时式(2)所表示的曲面与k-e坐标平面的交线即“等向固结渗透系数线”。当土体发生剪切变形时,孔隙比及剪应力水平同时变化引起渗透系数的变化,土体渗透系数的变化轨迹如图7中“一般轨迹”所示。

Figure 7. Dimensional curve surface of permeability
图7. 数学模型的空间曲线形式

Figure 8. Calculated values and measured values of permeability
图8. 渗透系数的模型计算值与实测值对比
4.5. 模型拟合与验证
根据本文试验结果,计算式(3)中的参数a、b、c,得到试验土料的渗透系数公式为
 (5)
(5)
将式(5)计算结果与试验结果进行对比,图8表示了试样在300 kPa、500 kPa、900 kPa条件下的对比结果。可以看出,模型计算结果与实测值较为接近,表明上述数学模型是有效的。
5. 结论
通过本文研究可得到如下结论:
1) 基于三轴仪改进的渗透试验装置可有效用于测试试样在剪切变形过程中的渗透系数。
2) 试验结果表明,粘性土的渗透系数受诸多因素的影响,如轴向剪切应变、围压、渗透方向和渗透水压力等,其中,剪切应变和围压的影响最为显著。
3) 所提出的渗透系数数学模型一方面通过孔隙比反映土体物理状态变化对渗透性的影响,另一方面通过剪应力水平反映剪切引起的结构变化对土体渗透系数的影响。当土体仅发生等向固结时,渗透系数沿数学模型的退化形式“等向固结渗透系数线”发展,当土体发生剪切变形时,渗透系数随着“一般轨迹”运行。
4) 基于试验数据的模型拟合表明,所提出的数学模型可有效反映土体在剪切变形过程中不同物理力学状态条件下的渗透系数。
基金项目
本文得到国家自然科学基金:50879039的资助。
参考文献 (References)
- [1] Chu, J. (2002) Consolidation and Permeability Properties of Singapore Marine Clay. Journal of Geotechnical and Geoenvironmental Engineering, 128, 724-732.
- [2] Marshall, T.J. (1958) A Relation between Permeability and Size Distribution of Pores. European Journal of Soil Science, 9, 1-8.
- [3] Nishida, Y., Koike, H. and Nakagawa, S. (1971) Coefficient of Permeability of Highly Plastic Clays. Proceedings of the 4th Budapest Conference on Soil Mechanics and Foundation Engineering, Budapest, 12-15 October 1971, 127- 133.
- [4] Garcia, I., Lovell, C.W. and Altschaeffle, A.G. (1979) Pore Distribution and Permeability of Silty Clays. Journal of the Geotechnical Engineering Division, 105, 839-856.
- [5] Bryant, W.R. and Richardson, M.D. (1992) Permeability and Porosity of Clayey Sediments in Seismo-Acoustics. The Journal of the Acoustical Society of America, 92, 2308-2321.
- [6] Chan, H.T. and Kenney, T.C. (1973) Laboratory Investigation of Permeability Ratio of New Liskeard Varved Soil. Canadian Geotechnical Journal, 10, 453-472.
- [7] Carpenter, G.W. and Stephenson, R.W. (1986) Permeability Testing in the Triaxial Cell. Geotechnical Testing Journal, 9, 3-9.
- [8] 朱建华 (1989) 土坝心墙原状土的三轴渗透试验. 岩土工程学报, 4, 57-63.
- [9] 李平, 骆亚生 (2006) 饱和土的三轴渗透试验研究. 路基工程, 6, 32-33.
