Advances in Porous Flow
Vol.07 No.02(2017), Article ID:21158,8
pages
10.12677/APF.2017.72002
LBM Simulation of Pore-Throat Radius Variation Due to Particle Deposition
Xiaodong Han
CNOOC Ltd, Tianjin Branch, Tianjin

Received: Jun. 8th, 2017; accepted: Jun. 22nd, 2017; published: Jun. 28th, 2017

ABSTRACT
During the developing process of oil and gas reservoirs, particles deposited in pore-throats may result in the decrease of its effective radius and capability for fluid flowing through. For studying the influence of deposited particles on the pore-throat radius and its changing rule, the formula for calculating the effective radius is obtained based on the capillary model and theoretical derivation. Besides, sensitive analysis is conducted for various parameters. The simulation results show that, the effective radius of pore-throats gets smaller with the increase of deposited particle radius and the decreasing rate is higher at the bigger particle size; the closer the particle deposits from the inlet face, the smaller of the effective radius is; besides, the effective radius of the pore- throat will be much greater when the pore-throat has a bigger ratio value between the length and its width. In addition, a mathematical model for calculating the effective radius is proposed based on the regression fitting, which may provide a useful guidance for research on the formation damage.
Keywords:Porous Media, Particle Deposition, LBM, Capillary Model, Effective Radius
微粒沉积导致孔喉尺寸变化的Lattice Boltz-Mann模拟研究
韩晓冬
中海石油(中国)有限公司天津分公司,天津
收稿日期:2017年6月8日;录用日期:2017年6月22日;发布日期:2017年6月28日

摘 要
油气田开发过程中,微粒在孔喉内的沉积会导致孔喉有效尺寸减小,流体流动能力降低。为研究微粒沉积对孔喉尺寸的影响及孔喉尺寸变化规律,以毛管模型为基础,通过理论推导和LBM模拟结合的方法对微粒沉积后孔喉有效半径进行求解,并选取不同参数进行了敏感性分析。模拟结果显示,随微粒粒径的增大,孔喉有效半径减小,且微粒越大有效半径减小越快;微粒沉积位置越靠近入口端,孔喉有效半径越小;孔喉长度与宽度比值越大时,孔喉有效半径值越大。最后通过回归建立了微粒沉积后孔喉有效半径的计算数学模型,可对从微观尺度研究微粒沉积导致储层伤害起到一定的指导作用。
关键词 :多孔介质,微粒沉积,LBM,毛管模型,孔喉有效半径

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
多孔介质内微粒的侵入和沉积在油气田开发过程中广泛存在。例如,在钻井、完井和压裂等作业过程中,大量微粒会随作业流体进入地下在井壁沉积产生泥饼,部分微粒会随流体进入储层,在孔喉内发生沉积导致孔喉尺寸降低 [1] [2] ;另一方面,在注水驱替过程中,随注入水流入储层或从孔喉壁面脱落的微粒,随注入流体流动的过程中也会在流经孔喉发生沉积,导致孔喉尺寸减小,流体流动阻力增大 [3] [4] [5] [6] [7] 。微粒在孔喉内沉积后,在微观上体现为孔喉有效半径减小,导致渗流能力降低;在宏观上则表现为储层渗流能力降低,渗透率值减小,即导致储层伤害。
为了从微观角度对微粒沉积对孔喉尺寸的影响及其规律进行研究,本文通过理论推导加LBM模拟的方法对微粒沉积后孔喉的有效半径进行了模拟求解,并选取微粒粒径、微粒沉积位置以及孔喉长度与宽度比值三个参数进行敏感性分析,对孔喉有效半径随不同参数的变化规律进行了分析。最后在大量模拟计算的基础上回归得到了微粒沉积后孔喉有效半径的计算数学模型。
2. 微粒沉积后有效半径计算
流体在多孔介质中的流动为层流,且符合Poiseuille公式 [8] [9] ,对于单个孔喉满足下式:
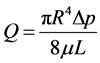 (1)
(1)
式中: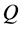 为孔喉内流体流速,
为孔喉内流体流速,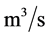 ;
;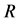 为孔喉半径,m;
为孔喉半径,m; 为孔喉两端压差,
为孔喉两端压差,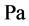 ;
;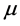 为流体粘度,
为流体粘度, ;
;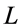 为孔喉长度,m。由式(1)可得:
为孔喉长度,m。由式(1)可得:
 (2)
(2)
孔喉微粒沉积示意图,如图1所示。
微粒在孔喉壁面沉积后,由于微粒的存在会对流体施加一个附加阻力,导致在相同流量条件下,
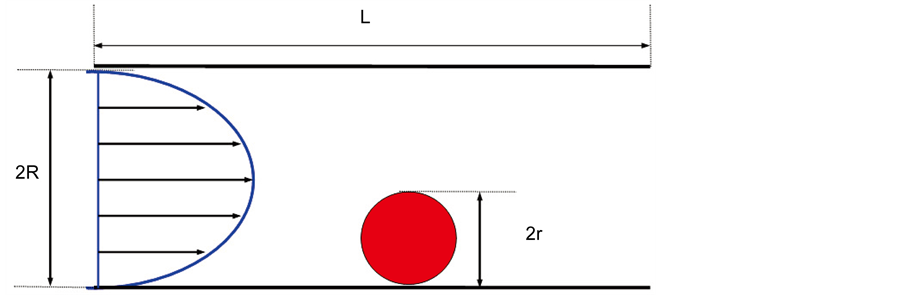
Figure 1. Schematic figure of particle depositing in pore-throat
图1. 孔喉微粒沉积示意图
孔喉两端压差增加,微粒沉积后孔喉两端压差计算如下式所示:
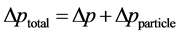 (3)
(3)
式中: 为无微粒时孔喉两端压差,
为无微粒时孔喉两端压差,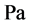 ;
;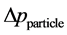 为由于微粒沉积导致的附加压差,
为由于微粒沉积导致的附加压差,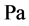 。
。
若假设微粒沉积后孔喉内流体流动依然符合Poiseuile公式,使用有效半径为 的毛管等效微粒沉积后毛管内流体的流动,则其有效半径值应满足:
的毛管等效微粒沉积后毛管内流体的流动,则其有效半径值应满足:
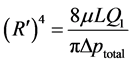 (4)
(4)
式中: 为微粒沉积后孔喉有效半径,m。
为微粒沉积后孔喉有效半径,m。
由式(2)和式(4)联立,在微粒沉积前后孔喉流量恒定(即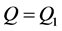 )的条件下,沉积后有效半径与原始半径比值满足:
)的条件下,沉积后有效半径与原始半径比值满足:
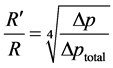 (5)
(5)
由式(5)可知微粒沉积后孔喉有效半径同原始半径的比值与其对应压差倒数的开四次方成正比。故在实际研究和计算微粒沉积对孔喉有效半径影响时,可以通过计算定流量条件下微粒沉积前后孔喉两端压差,进而根据式(5)进行求解。此处应用格子Boltzmann方法对不同条件下入口与出口间压差进行求解计算,进而对不同条件下有效半径的变化规律进行研究。
3. 格子Boltzmann方法模拟实现
格子Boltzmann方法由格子气自动机发展而来,由于其具有边界处理简单等优点,近十几年在多相流、传热等许多应用方面取得了长足发展 [10] [11] [12] [13] 。本文采用LBGK模型中的D2Q9模型对微粒沉积前后孔喉两端压差进行模拟计算,该模型每个格点处的速度配置如图2所示。
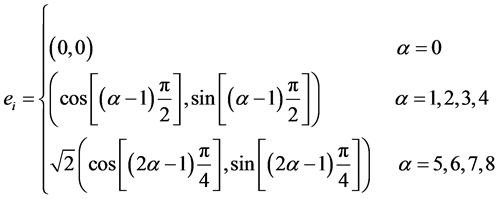 (6)
(6)

Figure 2. D2Q9 lattice structure model
图2. D2Q9模型速度分布
其演化方程为:
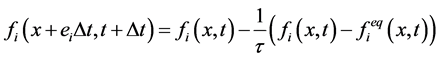 (7)
(7)
平衡态分布函数按下式计算:
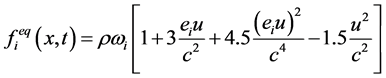 (8)
(8)
不同网格点处的宏观密度、宏观速度和压力值计算表达式如下所示:
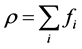 (9)
(9)
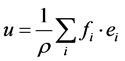 (10)
(10)
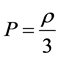 (11)
(11)
式中,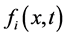 为
为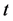 时刻格点
时刻格点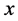 处沿
处沿 方向的粒子分布函数;
方向的粒子分布函数;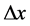 和
和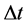 分别为空间步长和时间步长;
分别为空间步长和时间步长;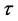 为松弛时间;权系数为
为松弛时间;权系数为 ,
, ,
, 。
。
进行模拟计算时,按图1中所示进行模型建立及网格划分。上下边界为孔喉固体壁面,设定为反弹
边界;左侧边界为流体入口,设为速度边界;右侧边界为流体出口,且边界处满足 。微粒壁面同
。微粒壁面同
样采用反弹边界,且模拟过程中微粒位置固定,不随流体运动。具体微粒沉积后有效半径计算步骤如下:
① 定x、y方向的网格数目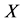 和
和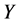 :由于网格步长相同,
:由于网格步长相同,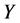 与
与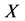 的比值即为孔喉的长度与宽度比;
的比值即为孔喉的长度与宽度比;
② 边界条件设置:上下边界为反弹边界,左右边界为速度边界且保持流体流量恒定;
③ 孔喉内无微粒时孔喉入口、出口间压差计算:应用式9和式11得到入口和出口处的压力值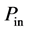 、
、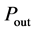 ,计算可得出入口与出口间压差为
,计算可得出入口与出口间压差为 ;
;
④ 将微粒添加进孔喉:设置微粒在孔喉内距入口的距离以及微粒半径值,微粒所在网格设置为固体边界,且微粒边界同样采用反弹边界;
⑤ 孔喉内有沉积微粒时孔喉入口、出口间压差计算:同样应用公式9和公式11得到入口和出口处的压力值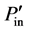 、
、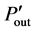 ,计算出入口与出口间压差为
,计算出入口与出口间压差为 ;
;
⑥ 微粒沉积后有效半径计算:在得到微粒沉积前后孔喉两端压差 和
和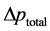 后,应用公式4即可计算得到微粒沉积后孔喉后有效半径与原始半径的比值
后,应用公式4即可计算得到微粒沉积后孔喉后有效半径与原始半径的比值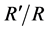 。
。
4. 不同因素下有效半径变化规律
通过之前的公式推导得到了微粒沉积前后孔喉有效半径的计算方法,并可以通过格子Boltzmann方法进行模拟实现。本节,通过选取对有效半径有较大影响的微粒和孔喉几何参数进行模拟计算,并分析不同参数对有效半径影响的变化规律。选取的主要参数为:微粒粒径、微粒沉积位置和孔喉长度与宽度比。
4.1. 微粒粒径的影响
模拟过程中其它条件保持不变,通过改变微粒的几何尺寸,对不同微粒粒径下的有效半径进行模拟求解,其中微粒位于入口和出口中间,具体结果如图3所示。图中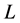 为孔喉长度,m;
为孔喉长度,m; 为孔喉半径,m。
为孔喉半径,m。
从图中可以看出,随着微粒粒径的不断增大,沉积微粒对孔喉的半径影响越大,导致有效半径值越小。且当微粒粒径从小逐渐增大过程中,孔喉的有效半径减小逐渐变快。
4.2. 微粒沉积位置的影响
模拟过程中通过改变微粒距入口端的距离即微粒在孔喉壁面的位置,对不同微粒位置处的有效半径进行模拟求解,孔喉的长宽比 ,具体结果如图4所示。图中
,具体结果如图4所示。图中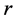 为微粒半径,m;
为微粒半径,m;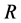 为孔喉半径,m。
为孔喉半径,m。
从图中可以看出,微粒距孔喉入口端越近,孔喉的有效半径值越小,即微粒沉积时越靠近入口端,沉积微粒对孔喉的伤害程度越大。且从图中可以看出有效半径随微粒位置的变化曲线具有较好的线性关系。
4.3. 孔喉长宽比的影响
模拟过程中其它参数保持不变,只改变孔喉的长度,对不同孔喉长宽比对有效半径的影响规律进行模拟分析,其中微粒位于孔喉中间,具体模拟结果如图5所示。图中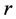 为微粒半径,m;
为微粒半径,m;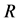 为孔喉半径,m。
为孔喉半径,m。
从图5中可以看出,在其它条件保持不变的情况下,随孔喉长宽比的逐渐增大,微粒沉积后有效半径值逐渐增大。即孔喉长宽比越大,沉积微粒对孔喉半径的伤害程度越小。同时可以看出,有效半径随孔喉长宽比的变化曲线同样具有较好的线性关系。
5. 孔喉有效半径计算模型
为实现对不同微粒沉积条件下孔喉有效半径的计算,以及微粒沉积导致多孔介质孔隙度、渗透率等宏观参数变化规律的模拟,本节通过对不同条件下有效半径值进行模拟计算,并通过多元回归方法 [14] 建立有效孔喉半径的计算数学模型,其中选取的拟合参数包括:微粒粒径、微粒沉积微粒和孔喉长宽比。
在大量模拟计算的基础上,通过多元回归得到的微粒沉积后孔喉有效半径计算数学模型如下:
 (12)
(12)
 (13)
(13)
式中: 为微粒沉积后有效半径,m;
为微粒沉积后有效半径,m;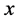 为微粒沉积位置距孔喉入口段的距离,m;
为微粒沉积位置距孔喉入口段的距离,m;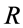 为孔喉半径,m;
为孔喉半径,m;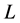 为孔喉长度,m。
为孔喉长度,m。
国外部分学者研究认为,当微粒半径大于孔喉半径的 时,微粒会通过多微粒架桥堵塞的方式将其沉积的孔喉堵塞,导致该孔喉失去连通性 [15] [16] 。故该处所建立模型主要用于
时,微粒会通过多微粒架桥堵塞的方式将其沉积的孔喉堵塞,导致该孔喉失去连通性 [15] [16] 。故该处所建立模型主要用于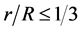 时孔喉有效半径的计算。
时孔喉有效半径的计算。
为验证拟合得到的数学模型的准确性,对模拟计算得到的有效半径值与应用式(12)和(13)得到的估计值进行对比,具体对比结果如表1所示。
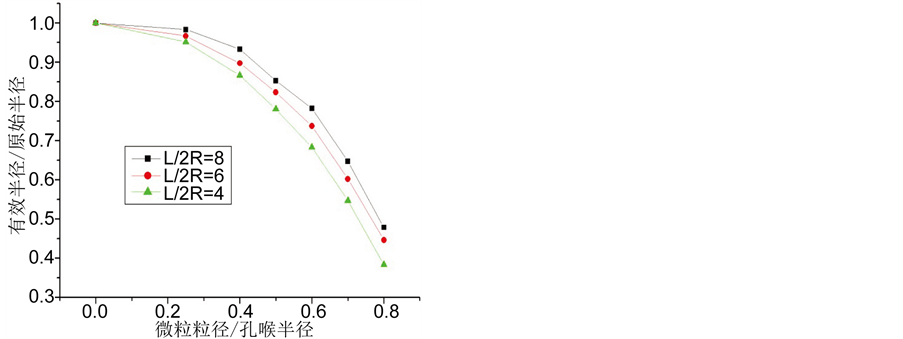
Figure 3. Effective radius vs ratio between particle radius and the pore-throat radius
图3. 微粒粒径与孔喉半径比值对有效半径的影响

Figure 4. Effective radius vs location of the deposited particle
图4. 微粒位置对有效半径的影响
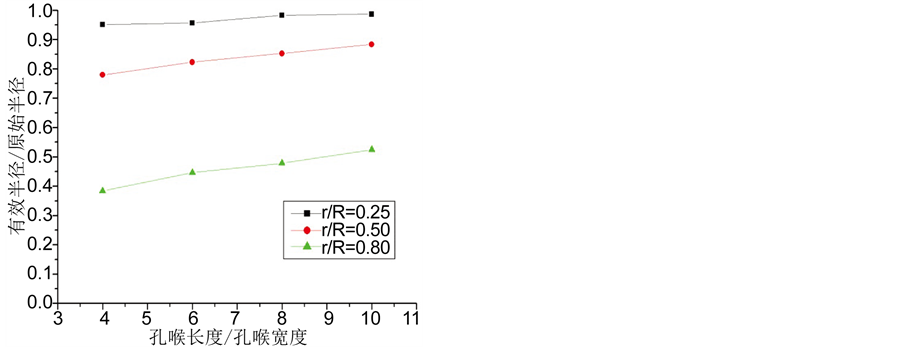
Figure 5. Effective radius vs ratio between the length and the width of the pore-throat
图5. 孔喉长宽比对有效半径的影响
Table 1. Comparison between the simulated effective radius and predicted value
表1. 有效半径的模拟计算值和式13估计值对比
从表l中数据可知,公式估计值与模拟计算值之间吻合度较高,拟合误差小于1.0%,故利用该数学模型计算微粒沉积后孔喉的有效半径值具有较高的可靠性。
6. 结论
1) 以毛细管模型为基础推导了微粒沉积后孔喉有效半径的计算公式,得到有效半径与原半径比值的四次方与对应压差比值呈反比;且应用格子Boltzmann方法对孔喉有效半径进行模拟求解可行。
2) 通过模拟结果得出:沉积微粒粒径越大,孔喉有效半径越小;微粒沉积位置越靠近孔喉入口端,孔喉的有效半径越小;微粒的长度和宽度之比越小,微粒沉积后孔喉有效半径越小。也就是说,微粒粒径越大、微粒越靠近孔喉入口段、孔喉长度越短,微粒沉积导致的伤害程度越大,孔喉有效半径越小。
3) 在大量模拟的基础上,通过回归得到了微粒沉积后孔喉有效半径的计算模型。通过对比公式估算值及模拟值确定该计算模型能较好地对微粒沉积后有效半径进行预测计算。
基金项目
国家科技重大专项“海上稠油油田热采技术试验示范”(2011ZX05057-005)。
文章引用
韩晓冬. 微粒沉积导致孔喉尺寸变化的Lattice Boltz-Mann模拟研究
LBM Simulation of Pore-Throat Radius Variation Due to Particle Deposition[J]. 渗流力学进展, 2017, 07(02): 13-20. http://dx.doi.org/10.12677/APF.2017.72002
参考文献 (References)
- 1. 冯其红, 韩晓冬, 王守磊, 等. 注入水中悬浮微粒导致储层伤害网络模拟研究[J]. 西南石油大学学报: 自然科学版, 2014, 36(3): 179-184.
- 2. 苏崇华. 疏松砂岩油田生产过程中储层伤害机理研究[J]. 中国海上油气, 2009, 21(1): 31-34.
- 3. 刘义坤, 冯树义, 刘云龙, 等. 卫星油田储层敏感性分析[J]. 大庆石油学院学报, 2007, 31(5): 51-54.
- 4. 胡雪滨, 徐永高. 油田注入水引起储层伤害的试验评价[J]. 江汉石油学院学报, 2002, 24(3): 53-55.
- 5. Khlar, K.C. and Fogler, H.S. (1983) Water Sensitivity of Sandtones. SPEJ, 23, 55-64. https://doi.org/10.2118/10103-PA
- 6. Rege, S.D. and Fogler, H.S. (1987) Network Model for Straining Dominated Particle Entrapment in Porous Media. Chemical Engineering Science, 42, 1553-1564. https://doi.org/10.1016/0009-2509(87)80160-4
- 7. Jalel, O. and Jean-Francois, V. (1999) A Two-Dimensional Network Model to Simulate Permeability Decrease Under Hydrodynamic Effect of Particle Release and Capture. Transport in Porous Media, 37, 303-325. https://doi.org/10.1023/A:1006690700000
- 8. 秦积舜, 李爱芬. 油层物理学[M]. 东营: 中国石油大学出版社, 2006.
- 9. 刘忠玉, 乐金朝, 苗天德. 无粘性土中管涌的毛管模型及其应用[J]. 岩石力学与工程学报, 2004, 23(22): 3871-3876.
- 10. 张浩龙, 陶实, 郭照立. 振动纤维补集颗粒的格子Boltzmann模拟[J]. 计算物理, 2016, 33(3): 311-320.
- 11. 姚军, 赵建林, 张敏, 等. 基于格子Boltzmann方法的页岩气微观流动模拟[J]. 石油学报, 2015, 36(10): 1280- 1289.
- 12. 朱益华, 陶果, 方伟. 基于格子Boltzmann方法的储层岩石油水两相分离数值模拟[J]. 中国石油大学学报(自然科学版), 2010, 34(3): 48-52.
- 13. 赵金洲, 符东宇, 李永明, 等. 基于格子Boltzmann方法的页岩气藏气体滑脱效应分析[J]. 油气地质与采收率, 2016, 23(5): 65-70.
- 14. 袁迎中, 张烈辉, 何磊, 等. 注采比多远回归分析及合理注采比的确定[J]. 石油天然气学报, 2008, 30(1): 229- 302.
- 15. Choo, C.-U. and Tien, C. (1995) Simulation of Hydrosol Deposition in Granular Media. A.I.Ch.E. Journal, 41, 1426- 1442. https://doi.org/10.1002/aic.690410609
- 16. Gao, C.H. (2008) Understanding Capture of Non-Brownian Particles in Porous Media with Network Model. Asia-Pacific Journal of Chemical Engineering, 3, 298-306. https://doi.org/10.1002/apj.149
