基于遗传算法的生鲜超市水果库存控制研究 Research on Inventory Control of Fresh Supermarket Fruit Based on Genetic Algorithm

doi:10.12677/MSE.2019.82015

Management Science and Engineering
Vol. 08 No. 02 ( 2019 ), Article ID: 29586 , 11 pages
10.12677/MSE.2019.82015

Research on Inventory Control of Fresh Supermarket Fruit Based on Genetic Algorithm

Ai Zhang, Jianqin Zhou

●How to Cite this Article

School of Economics and Management, Beijing Jiaotong University, Beijing

Received: Mar. 13^th, 2019; accepted: Mar. 28^th, 2019; published: Apr. 4^th, 2019

ABSTRACT

With the gradual improvement of people’s consumption level, people’s demand for healthy, nutritious and safe fruits and vegetables has become increasingly high. At the same time, they turned to be too picky on the freshness of the fruits and vegetables, which makes it harder for the administrator to operate the fruit with seasonal, perishability and short shelf life. The operating profit of fresh supermarket is largely determined by the inventory control level, and the scientific and effective inventory control strategy is an effective way to improve the inventory management level of fresh supermarket. This paper constructs an inventory control model considering the characteristics of fresh supermarket business hours and consumer demand affected by price and freshness. Then combined with the S fresh supermarket American cherry sales data as an example, the genetic algorithm of binary coding is used to solve the model. The sale profit increased 13.7% which achieved the rationality of fruit inventory control.

Keywords:Fresh Fruit, Inventory Control, Genetic Algorithm

基于遗传算法的生鲜超市水果库存控制研究

张爱，周建勤

北京交通大学经济管理学院，北京

收稿日期：2019年3月13日；录用日期：2019年3月28日；发布日期：2019年4月4日

摘要

随着人们消费水平逐渐提高，人们对健康、营养、安全的果蔬品的需求日益高涨，对果蔬的新鲜度等愈加挑剔，从而增大了水果这种易变质、货架期短的生鲜农产品在生鲜超市的运营难度。生鲜超市的经营收益在很大程度上是由库存控制水平决定的，而科学有效的库存控制策略是提高库存管理水平的有效途径。本文考虑生鲜超市营业时间分段、消费者需求受价格和新鲜度影响的特点构建了库存控制模型，并结合S生鲜超市美国车厘子销售实例采用二进制编码的遗传算法对模型进行求解，销售利润提升了13.7%，实现了超市水果库存控制的合理性。

关键词 :生鲜水果，库存控制，遗传算法

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

近年来随着人们消费水平的逐渐提高，人们对健康、营养、安全的果蔬品的需求日益高涨，对果蔬的新鲜度等愈加挑剔，从而增大了水果这种易变质、货架期短、季节性强的生鲜农产品在生鲜超市的运营难度，如何在提高消费者满意度的同时又能最大程度的避免水果滞销损耗或者缺货等库存问题的困扰，整体上提高生鲜超市的销售利润是目前生鲜超市经营水果亟需解决的问题。

在日常超市的经营过程中，生鲜超市的水果采购人员对于水果的库存不能及时做到每日盘点，对于库存管理的意识不高，在每天订货时完全是依靠自己的工作经验，一方面由于自己的经验不足对于订购周期和订购数量难以把控，另一方面由于经营水果种类繁多，缺乏相应管理信息系统的支持对市场需求进行精准预测，因此导致的水果缺货、滞销损耗现象较为严重，由于库存策略的缺失间接导致生鲜超市的销售利润较低，一般在4%到7%的范围内波动。因此为了保证正常经营减少水果损耗，生鲜超市需要提高库存管理水平，优化库存控制策略。

2. 易腐品库存控制研究现状

最早研究易腐品库存问题的是美国学者Whitin (1957) [1] ，他提出时尚服装在库存周期末应该降价处理，并对相应的EOQ模型进行了探讨。在此之后Ghare和schrader (1963) [2] 研究了变质率为常数，需求率为时间的线性函数的库存控制模型,通过模型求解来表示易变质产品逐渐衰减的过程。后来学者关于易变质产品的库存控制模型大多是在它的基础上展开的。励凌峰、黄培清等(2004) [3] 首次提出变质率和需求率存在一定的数量关系，并研究了有限时域内的库存控制模型，以迭代逼近的算法来求解最优的订购批量和订货周期。王淑云等(2015) [4] 以整个供应链上的销售利润最大化来研究易变质产品的库存决策问题。段永瑞等(2014) [5] 站在零售商的角度，假设需求依赖于货架区的库存，以平均销售总利润最大化为目标函数，决策变量为订购量与订购点在此基础上建立了易变质品库存控制模型。Donselaar K.V. (2006) [6] 等人提出针对生鲜农产品的订货，如果硬件条件以及数据支持，那么门店应该采用自动订货系统来进行库存控制。张青山(2015) [7] 提出订货是损耗控制的源头，只有科学合理的订货，才能做到把紧损耗控制的大门。陈军、但斌(2009) [8] 等人研究了基于流通损耗控制下的生鲜农产品订货策略，他们提出零售商为了降低新鲜度的衰减对顾客造成的满意度的影响，应该采取多级价格折扣的方式来刺激消费者的购买欲望。刘月(2018) [9] 等考虑了货架期、变质期和订货提前期之间的关系，以零售商单个订货周期内的销售利润最大化为目标，考虑销售时间段的影响构建了库存控制模型，并设计相应的算法进行求解。德新玲(2012) [10] 介绍了货架期理论，他认为货架期在某种程度上可以表示变质率的大小，并根据变质率的不同表达形式得出了货架期和变质率的三种数学具体表达式，并在此基础上构建了需求为常数的生鲜品库存控制模型。樊华(2015) [11] 从定性的角度出发，通过实际调研分析影响超市生鲜食品库存管理的因素，提出了超市应该深化经营品类的分析、做到经常盘点库存、实施供应商管理库存以及加大开放式的管理信息系统的平台建设等建议。

国内外学者针对易腐品库存管理问题进行了广泛的研究，通过需求率、变质率、是否允许价格折扣、是否允许缺货等不同形式的组合来建立模型，为了自己研究问题的创新来简化相关条件，最后得出相应结论，但是现有研究中综合考虑超市营业时间特点以及消费者需求受新鲜度影响的较少。本文根据影响水果库存管理水平的因素，从需求和变质特性对库存水平的变化进行分析，基于Ghare和Schrader [2] 的经典易变质产品库存管理模型，考虑消费者需求受价格和新鲜度影响的，超市营业时间分段的特点，构建生鲜超市水果库存控制模型，然后设计遗传算法对库存控制模型进行求解。

3. 生鲜超市水果库存控制模型构建

3.1. 问题描述

本文研究具有一定销售周期的季节性水果，生鲜水果不同于其他一般商品，货架期最长的为十几天，最短的为2天，腐烂速率非常快。在超市进行销售时有具体的货架期标准，货架期为。水果超出货架期后失去销售价值，立马下架报损。根据生鲜超市水果的易腐性和销售特点，分别描述水果在需求、定价等方面的特殊性，并以此作为模型建立的基础。

生鲜水果的需求受价格和新鲜度变化，因此假设需求是价格和新鲜度的函数。

实际生活中，生鲜超市并不像便利店一样24小时营业，分为营业时间段和非营业时间段。超市营业时间为t₁，一个销售日是一天。在[0, t₁]时间段内超市不营业，[t₁, 1]在时间段内超市营业。在非营业时间段内，消费者的需求为0，但是变质一直在发生，因此消费者的需求是一个分段函数，库存水平表达式也是一个分段函数。

频繁变价是大多数生鲜超市销售的主要特点。一般情况下超市会采用周期性定价的方式，定价周期为1~2天。本文考虑价格为决策变量，考虑天天定价的库存控制模型，使得生鲜超市销售利润最大化。

3.2. 模型假设

1) 水果的订货周期为n，在第n天通过调价或者扔掉使得当日结束时库存为0。

2) 假设不允许缺货，即当库存量将为0时，生鲜水果采销负责人在该天销售结束时立即发出订单通知，发出订货请求后供应商凌晨送货到门店。

3) 水果在超市进行销售时变质速率为常数θ。

4) 一个订货周期内的各项采购成本、单次订购的固定成本、单位库存持有成本不发生变化且为常数。

3.3. 参数说明

1) 决策变量

n：订货周期；

p_w：第w个销售日的销售价格；

2) 主要参数

L：水果的销售时间长度；

n：订货周期；

m：水果的货架期；

Q：订购批量；

t：一个销售日的销售时刻；

t₁：超市开始营业时间点；

θ：水果的变质率；

β：水果最初到达超市的新鲜度；

w：第w个销售日；

q_w:第w个销售日的初始库存量；

I_w(t)：第w个销售日t时刻的库存量；

D_w(t):第w个销售日t时刻的需求量；

H_w(n)：第w个销售日的库存持有成本；

H(n)：总库存持有成本；

R_w(n)：第w个销售日的销售收入；

R(n)：总销售收入；

$π (n, p_{1}, p_{2}, p_{3}, \dots, p_{n})$ ：总销售利润；

p₀：水果的平均市场销售价格；

C_b：单位水果的采购价格；

C_h：单位水果的库存持有成本；

C_d：每次订货的固定成本；

C_r:线下渠道运营成本；

C_o：线上渠道运营成本；

η：客流量限制因子。

3.4. 模型构建

参考Ghare的经典易变质品库存控制模型，库存水平函数与变质率和需求率之间的关系可以表示为：

$\frac{d I (t)}{d t} = - θ (t) I (t) - D (t)$ (1)

第w个销售日的需求函数表达式为：

$D_{w} (t) = {\begin{cases} (a - b p_{w}) β^{(w - 1) + t} t_{1} \leq t \leq 1 \\ 0 0 \leq t \leq t_{1} \end{cases}$ (2)

则第w个销售日t时刻的的库存水平表达式为：

$\frac{d I (t)}{d t} = {\begin{cases} - θ I_{w} (t) - (a - b p_{w}) β^{(w - 1) + t} t_{1} \leq t \leq 1 \\ - θ I_{w} (t) 0 \leq t \leq t_{1} \end{cases}$ (3)

对上式进行积分得：

$I_{w} (t) = {\begin{matrix} \frac{(b p_{w} - a) β^{(w - 1) + t}}{\ln β + θ} + c_{1} e^{- θ t} t_{1} \leq t \leq 1 \\ c_{2} e^{- θ t} 0 \leq t \leq t_{1} \end{matrix}$ (4)

根据模型假设可以得出来，第w个销售日 $t = 0$ 时刻的库存水平就是该天的初始库存量，即有 $I_{w} (0) = q_{w}$ ，代入公式(4)求得： $c_{2} = q_{w}$

$\frac{(b p_{w} - a) β^{(w - 1) + t_{1}}}{\ln β + θ} + c_{1} e^{- θ t_{1}} = q_{w} e^{- θ t_{1}}$ (5)

$\begin{array}{l} c_{1} = \frac{1}{\ln β + θ} (a e^{θ t_{1}} β^{(w - 1) + t_{1}} - b p_{w} e^{θ t_{1}} β^{(w - 1) + t_{1}} + \ln β q_{w} θ q_{w}) \\ = \frac{e^{θ t_{1}} (a - b p_{w}) β^{^{(w - 1) + t_{1}}}}{\ln β + θ} + q_{w} \end{array}$ (6)

将c₁和c₂代入（4）式后整理得到：

$I_{w} (t) = {\begin{matrix} q_{w} e^{- θ t} + \frac{(b p_{w} - a)}{\ln β + θ} β^{(w - 1)} [β^{t} - β^{t_{1}} e^{- θ (t - t_{1})}] t_{1} \leq t \leq 1 \\ q_{w} e^{- θ t} 0 \leq t \leq t_{1} \end{matrix}$ (7)

注意到 $β = e^{\ln β}$ 是等价的，因此

$I_{w} (t) = {\begin{matrix} q_{w} e^{- θ t} + \frac{(b p_{w} - a)}{\ln β + θ} [e^{[(w - 1) + t] \ln β} - e^{(w - 1) \ln β + (\ln β + θ) t_{1} - θ t}] t_{1} \leq t \leq 1 \\ q_{w} e^{- θ t} 0 \leq t \leq t_{1} \end{matrix}$ (8)

由于第w个销售日 $t = 1$ 时刻等于第 $w + 1$ 个销售日 $t = 0$ 时刻的库存水平，可以得到：

$\begin{array}{l} q_{w + 1} = \frac{e^{- θ}}{\ln β + θ} (q_{w} (\ln β + θ) - (a - b p_{w}) (e^{w \ln β + θ} - e^{θ t_{1} + \ln β [(w - 1) + t_{1}]})) \\ = \frac{e^{- θ}}{\ln β + θ} (q_{w} (\ln β + θ) - (a - b p_{w}) e^{w \ln β} (e^{θ} - e^{θ t_{1} + \ln β [- 1 + t_{1}]})) \\ = q_{w} e^{- θ} - \frac{(1 - e^{(- \ln β) (1 - t_{1}) - θ (1 - t_{1})}) ((a - b p_{w}) e^{w \ln β})}{i n β + θ} \end{array}$ (9)

利用变换 $X = e^{- (1 - t_{1}) \ln β}; Y = e^{- θ (1 - t_{1})}; Z = \frac{1 - X Y}{\ln β + θ}$

得出

$q_{w + 1} = q_{w} e^{- θ} - Z (a - b p_{w}) e^{w \ln β}$

根据数学归纳法可以得出：

$q_{1} = Q$ ；

$q_{2} = Q e^{- θ} - Z (a - b p_{1}) e^{\ln β}$

$\begin{array}{l} q_{3} = (Q e^{- θ} - Z (a - b p_{1}) e^{\ln β}) e^{- θ} - Z (a - b p_{2}) e^{2 \ln β} \\ = Q e^{- 2 θ} - Z (a - b p_{1}) e^{\ln β - θ} - Z (a - b p_{2}) e^{2 \ln β} \end{array}$

$\begin{array}{l} q_{4} = (Q e^{- 2 θ} - Z (a - b p_{1}) e^{(\ln β - θ)} - Z (a - b p_{2}) e^{2 \ln β}) e^{- θ} - Z (a - b p_{3}) e^{3 \ln β} \\ = Q e^{- 3 θ} - Z (a - b p_{1}) e^{(\ln β - 2 θ)} - Z (a - b p_{2}) e^{(2 \ln β - θ)} - Z (a - b p_{3}) e^{3 \ln β} \\ = Q e^{- 3 θ} - Z [(a - b p_{1}) e^{(\ln β - 2 θ)} - (a - b p_{2}) e^{(2 \ln β - θ)} -] (a - b p_{3}) e^{3 \ln β} \end{array}$

从而得到第w个销售日的初始库存水平表达式为：

$q_{w} = {\begin{matrix} Q_{e}^{- (w - 1) θ} - Z \sum_{i = 2}^{w} (a - b p_{i - 1}) e^{(i - 1) \ln β - (w - i) θ} & w = {2, 3, 4, \dots, n} \\ Q & w = 1 \end{matrix}$ (10)

由每个订货周期末的库存量为0可以得出： $I_{n} (1) = 0$ ，分别带入公式(7)和公式(10)得出：

$Q = Z \sum_{w = 1}^{n} (a - b p_{w}) e^{w (\ln β + θ)} ， 1 \leq n \leq m$ (11)

$q_{w} = Z e^{- (w - 1) θ} \sum_{i = w}^{n} (a - b p_{w}) e^{i (\ln β + θ)} ， {w = 1, 2, \dots, n}$ (12)

第w个销售日的库存持有成本如下：

$\begin{array}{l} H_{w} (n) = C_{h} (\int_{0}^{1} q_{w} e^{- θ} d t + \int_{t_{1}}^{1} \frac{a - b p_{w}}{\ln β + θ} [e^{(w - 1) \ln β + (\ln β + θ) t_{1} - θ t} - e^{(w - 1) \ln β + t}] d t) \\ = C_{h} [\frac{q_{w} (1 - e^{- θ})}{θ} - \frac{(a - b p_{w}) e^{w \ln β}}{\ln β + θ} (\frac{1 - X}{\ln β} - \frac{X (1 - Y)}{θ})] \end{array}$

总库存持有成本如下：

$H (n) = \sum_{w = 1}^{n} H_{w} (n) = C_{h} [\sum_{w = 1}^{n} \frac{q_{w} (1 - e^{- θ})}{θ} - \sum_{w = 1}^{n} \frac{(a - b p_{w}) e^{w \ln β}}{\ln β + θ} (\frac{1 - X}{\ln β} - \frac{X (1 - Y)}{θ})]$ (13)

第w个销售日的销售收入如下：

$R_{w} (n) = \int_{0}^{1} p_{w} D (p_{w}, t) d t = \int_{t_{1}}^{1} p_{w} (a - b p_{w}) β^{(w - 1) + t} d t = \frac{1 - X}{\ln β} p_{w} (a - b p_{w}) e^{w \ln β}$

总销售收入如下：

$R (n) = \sum_{w = 1}^{n} R_{w} (n) = \frac{1 - X}{\ln β} \sum_{w = 1}^{n} p_{w} (a - b p_{w}) e^{w \ln β}$ (14)

总销售利润如下：

$π (n, p_{1}, p_{2}, p_{3}, \dots, p_{n}) = R (n) - H (n) - C_{b} Q - C_{d} - C_{o} - C_{_{r}}$ (15)

则整个销售周期内的总销售利润如下：

$π_{L} (n, p_{1}, p_{2}, p_{3}, \dots, p_{n}) = \frac{L}{n} [R (n) - H (n) - C_{b} Q - C_{d} - C_{o} - C_{r}]$ (16)

针对生鲜超市来说，由于不能出现亏本的情况，所以每日的销售价格不能低于采购成本，另一方面超市水果销售具有提升客流量的作用。超市在进行订货时，从采购者的角度分析，预估水果有一个最低需求量来进行订货，以市场平均价格下的一般需求量为参照，可以得出，第w天的销售量大于一般需求量，参照杨文艺 [12] 对于客流量限制因子的描述，得出如下约束条件：

$Q_{w} \geq η Q_{0}$

$Q_{w} = \int_{t_{1}}^{1} (a - b p_{w}) β^{(w - 1) + t} d t = \frac{1 - X}{\ln β} (a - b p_{w}) e^{w \ln β}$ (17)

$Q_{0} = \int_{t_{1}}^{1} (a - b p_{0}) β^{(w - 1) + t} d t = \frac{1 - X}{\ln β} (a - b p_{0}) e^{\ln β}$ (18)

综上可以得到约束条件为：

$C_{b} \leq P_{w} \leq \frac{a}{b} - \frac{η}{b} (a - b p_{0}) β^{- (w - 1)}$ (19)

由超市实际运作情况可知，订货周期 $n \leq$ 货架期m

最终总的利润函数和约束条件为：

$\begin{array}{l} \max π_{L} (n, p_{1}, p_{2}, p_{3}, \dots, p_{n}) \\ = \frac{L}{n} [\frac{1 - X}{\ln β} \sum_{w = 1}^{n} p_{w} (a - b p_{w}) e^{w \ln β} + C_{h} \frac{Z (1 - e^{- θ})}{θ} \sum_{w = 1}^{n} \sum_{i = w}^{n} (a - b p_{w}) e^{i (\ln β + θ)} e^{- w θ} \\ + C_{h} (\frac{1 - X}{\ln β} - \frac{X (1 - Y)}{θ}) \sum_{w = 1}^{n} \frac{(a - b p_{w}) e^{w \ln β}}{\ln β + θ} + C_{h} (\frac{1 - X}{\ln β} - \frac{X (1 - Y)}{θ}) \sum_{w = 1}^{n} \frac{(a - b p_{w}) e^{w \ln β}}{\ln β + θ}] \end{array}$

为了简化目标函数，记

$\begin{array}{l} α_{1} = \frac{L}{n} (\frac{1 - X}{\ln β}) α_{2} = \frac{L}{n} C_{h} \frac{Z (1 - e^{- θ})}{θ} α_{3} = \frac{L}{n} C_{h} (\frac{1 - X}{\ln β} - \frac{X (1 - Y)}{θ}) \\ α_{4} = \frac{L}{n} C_{b} Z α_{5} = C_{d} + C_{o} + C_{r} \end{array}$

则最终利润函数表达式为

$\begin{array}{l} \max π_{L} (n, p_{1}, p_{2}, p_{3}, \dots, p_{n}) = α_{1} \sum_{w = 1}^{n} p_{w} (a - b p_{w}) e^{w \ln β} + α_{2} \sum_{w = 1}^{n} \sum_{i = w}^{n} (a - b p_{w}) e^{i (\ln β + θ)} e^{- w θ} \\ + α_{3} \sum_{w = 1}^{n} \frac{(a - b p_{w}) e^{w \ln β}}{\ln β + θ} - α_{4} \sum_{w = 1}^{n} (a - b p_{w}) e^{w (\ln β + θ)} - α_{5} \end{array}$ (20)

约束条件为：

${\begin{cases} C_{b} \leq P_{w} \leq \frac{a}{b} - \frac{η}{b} (a - b p_{0}) β^{- (w - 1)} \\ n \leq m, 且为整数 \end{cases}$ (21)

3.5. 遗传算法求解

在库存控制策略中，建立的总利润最大化模型应该考虑的是全局最优化，现在全局最优化的算法有遗传算法与模拟退火算法等。在这些算法中，近年来研究最成熟发展最快的是遗传算法 [13] 。该方法是启发式算法中的一种，也是一种随机搜索算法。因此本文在对水果库存控制模型进行求解时采用遗传算法。

1) 遗传编码

本文处理的是生鲜超市水果库存管理问题，涉及到的订货周期和价格向量取值有限，由于二进制编码的效果较好，而本文涉及到的变量处理中有小数的存在，选择二进制编码的效果会由于其他编码方式，如实数编码等。因此本文在对模型进行求解时选取二进制编码的方式来进行处理。

2) 产生初始群体

初始群体一般通过随机方法产生，初始群体的规模依经验决定，另外还需要保持群体的多样性。

3) 构建适应函数

适应函数构成了个体的生存环境，比较每个个体的适应值，判断其生存能力。适应函数值越高，表示染色体越符合目标。对于函数优化问题，可以将目标函数定义为适应度评价函数，将函数优化中的目标函数映射成求最大值形式的函数。由于本文目标函数是求最大值的函数，所以可以建立如下适应函数 $g (x) = f (x)$ 。本文中的适应度函数为最大利润的模型函数，其中适应度函数的目标为最大化利润，优化的变量为订货周期n和价格p。以目标的最优化即利润最大化为优化方向，对目标进行优化。

4) 遗传算子

遗传操作包括选择、交叉和变异三个遗传算子 [13] 。这三种形式构成了遗传算法强大搜索能力的核心。选择是指从群体中选择优胜的个体，淘汰劣质个体。选择的目的是把优化的个体(或解)直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。交叉算子使得遗传算法的搜索能力得到了很大程度的提高。一般建议交叉概率 $P_{c}$ 取值范围为0.4~0.99。变异是交叉后子代发生的变异，是子代基因发生的小概率变化，其算法包括：实值变异和二进制变异，一般建议取值范围为0.0001~0.1。

相应的遗传算法流程如下图1所示：

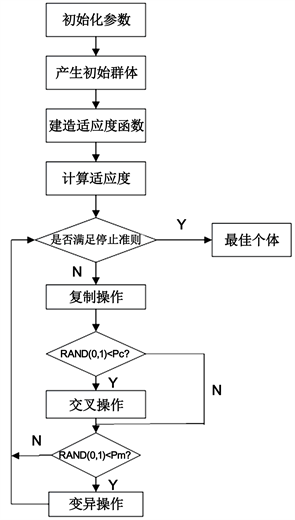
Figure 1. Basic operation flow of genetic algorithm

图1. 遗传算法基本操作流程

4. 生鲜超市水果库存控制方案应用

4.1. 遗传算法求解

本文将其求解过程分为四个步骤，分别为对相关参数进行编码、确定初始种群、设定适应度函数、设计遗传操作等，具体应用步骤如上节描述所示，相关编码如下表1所示：

Table 1. Initial parameter setting for GA

表1. 遗传算法初始参数设定

4.2. 算例分析

以S生鲜超市2018年6月1日至7月30日在售的美国车厘子为例，第一周的日均销售量以及订购量如下表2所示：

Table 2. Order and pricing of cherries

表2. 车厘子订货及定价情况

目前S生鲜超市在进行订货时，订货数量以及订货周期具有盲目性，在6月1日至7日采取每天都订货的方式，订货数量不固定，由于美国车厘子的货架期为3天，由上述表中数据可以看出，6月1日至3日总共订货300盒，按照先进先出的方式进行售卖，截止到6月5日，总共销售200盒，下架报损100盒，由此可以看出S生鲜超市在订货周期和订货批量上没有科学的管理方式，销售价格没有根据货架期临近时的质量情况或者市场价格来及时进行调整，导致损耗率较大，经营利润较低，甚至会出现负毛利的情况。

根据销售报表数据整理得出，6月1日至7月30日S生鲜超市在对车厘子进行订货时订货周期为1天，订货数量不固定，平均销售定价为51.8，销售毛利为7259.8元。

针对6月1日至7月30日美国车厘子销售的数据进行收集，并参考相关资料对参数数值进行修正，确保数据的普遍广泛性，具体参数含义与数值如下表3所示：

Table 3. Initial data of the example analysis

表3. 算例分析初始数据

采用Matlab编程计算出遗传算法结果如下图2所示。结果显示，当n = 2，价格变量取(49.8, 44.6)时，销售利润最大，最大利润为8254.3元，订货批量为80盒。

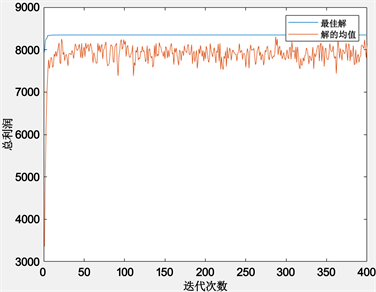
Figure 2. Convergence diagram between objective function and iteration number

图2. 目标函数与迭代次数收敛关系图

在对美国车厘子的订货周期和订货价格进行求解时，其种群适应度曲线呈现如上图趋势，随着迭代次数的增加，种群中个体的适应度呈现增长的趋势，且迭代次数越大其增长趋势越缓慢，逐渐趋于稳定，意味着将出现最优解。从图2中可以看出库存控制模型的目标函数遗传算法性能跟踪曲线图可以看出，经过400次迭代后，在20代左右遗传算法求解的目标函数值趋于稳定，可以计算出相应的目标函数最优解。

用该方案与S生鲜超市实际的经营数据相比较，总利润有所提高，上升了13.7%，证明了模型的有效性。虽然S生鲜超市在日常订货时每天订一次货，保证了美国车厘子的新鲜程度，但是由于订货次数较频繁，订货量比较大，没有根据实际车厘子的质量(货架期)情况动态调整价格，造成了订货费用较高，损耗率较大的情况，使得销售毛利比较低。因此本文模型的建立在一定程度上为S生鲜超市的订货策略和销售价格策略提供了一定的参考意见。

5. 结论

本文结合易变质品库存管理理论分析了影响水果库存管理的因素，然后考虑生鲜超市营业时间分段、非营业时间段的变质会对下一个销售日的需求产生影响的特点，构建了需求受价格和新鲜度影响的适合生鲜超市水果销售特点的库存控制模型。

本研究以S生鲜超市车厘子的实际经营数据作为算例，利用遗传算法进行求解，将模型计算出来的最大利润和实际经营利润作对比，验证了模型的有效性。并根据结果得出生鲜超市在销售水果时应该根据市场价格和货架期的特点及时动态调价，减少下架报损带来的损失。本文提出的模型可以为生鲜超市经营生鲜农产品的订货和定价提供一定的参考意见，以最大程度的降低损耗，实现生鲜水果科学的库存管理。

致谢

感谢导师对我论文耐心的指导，感谢S生鲜超市管理人员提供的数据，感谢舍友对我的帮助。

文章引用

张爱,周建勤. 基于遗传算法的生鲜超市水果库存控制研究
Research on Inventory Control of Fresh Supermarket Fruit Based on Genetic Algorithm[J]. 管理科学与工程, 2019, 08(02): 113-123. https://doi.org/10.12677/MSE.2019.82015

参考文献

1. Within, T.M. (1957) Theory of Inventory Management. Princeton University Press, Princeton, 62-72.

2. Ghare, P. and Schrader, G.F. (1963) A Model for an Exponentially Decaying Inventory. Industrial Engineering, 14, 238-243.

3. 励凌峰, 黄培清, 骆建文. 易腐物品的库存管理研究[J]. 系统工程, 2004, 22(3): 25-30.

4. 王淑云, 姜樱梅, 王宪杰. 变质率呈Weibull分布的一体化三级冷链库存策略研究[J]. 管理工程学报, 2015, 29(2): 229-239.

5. 段永瑞, 李贵萍, 霍佳震. 部分延迟订购的Weibull分布变质品库存策略研究[J]. 管理工程学报, 2013, 27(3): 205-213.

6. Donselaar, K.V., Woensel, T.V. and Broekmeulen, R. (2006) Inventory Control of Perishables in Supermarkets. International Journal of Production Economics, 104, 462-472.
https://doi.org/10.1016/j.ijpe.2004.10.019

7. 张青山. 超市生鲜损耗控制要点[J]. 今日零售, 2016(33): 42-43.

8. 陈军, 但斌, 曹群辉, 等. 短保质期变质产品的两次订货策略研究[J]. 管理科学学报, 2009, 12(3): 83-91.

9. 刘月. 零售终端生鲜农产品库存控制策略研究[D]: [硕士学位论文]. 天津: 天津理工大学, 2018.

10. 德新玲. 基于货架期的超市生鲜食品库存模型构建与策略研究[D]: [硕士学位论文]. 天津: 河北工业大学, 2012.

11. 樊华. 超市生鲜农产品库存管理研究[J]. 南方农业, 2015, 9(33): 136-137.

12. 杨文艺. 零售终端的冷鲜肉库存优化策略研究[D]: [硕士学位论文]. 北京: 北京交通大学, 2015.

13. 席裕庚, 柴天佑. 遗传算法综述[J]. 控制理论与应用, 1996(6): 697-701.

期刊菜单