Mechanical Engineering and Technology
Vol.06 No.02(2017), Article ID:20909,7
pages
10.12677/MET.2017.62013
Finite Element Modeling of Tower Bolt Connection and Dynamic Load Analysis
Ye Zhang1, Shengchun Wang2
1School of Mechanical and Electrical Engineering, Shandong University of Architecture, Jinan Shandong
2Main lab of Mechanical Engineering Innovation Technology of Shandong Province, Jinan Shandong

Received: May 23rd, 2017; accepted: Jun. 2nd, 2017; published: Jun. 9th, 2017

ABSTRACT
Considering the thread Angle to establish the three-dimensional finite element model of bolt connection, using ABAQUS finite element analysis, with the method of direct load exerted preload, simulation of the bearing capacity of the threaded connection vice, and compared with Yamamoto analytic method is used for validation. Applying transverse dynamic loads, on the basis of dynamic loads is studied under the action of thread pair of different friction coefficient of the corresponding changes of the bearing capacity of screw thread.
Keywords:Screw Pairs, Analytical Method, Transverse Dynamic Loads, Friction Coefficient, Bearing Capacity
塔机螺栓连接有限元建模及动态载荷分析
张烨,王胜春
1山东建筑大学机电工程学院,山东 济南
2山东省高校机械工程创新技术重点实验室,山东 济南
收稿日期:2017年5月23日;录用日期:2017年6月2日;发布日期:2017年6月9日

摘 要
考虑螺纹升角建立螺栓联接的三维有限元模型,利用ABAQUS进行有限元分析,采用直接加载的方式施加预紧力,模拟螺纹联接副的承载力,并与Yamamoto解析法进行了对比验证。在此基础上施加横向动态载荷,研究了动态载荷作用下螺纹副不同的摩擦系数对应的螺纹承载力的变化情况。
关键词 :螺纹副,解析法,横向动态载荷,摩擦系数,承载力

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
塔式起重机螺栓连接松动是塔机发生倾覆事故的原因之一。目前建筑工地上多数使用的塔机是自升式塔机,标准节是依靠高强度螺栓来连接固定的。塔式起重机在进行工地作业时,各个标准节是依靠螺栓预紧力使接合面产生摩擦力来承受的,塔身起着支撑上部工作部件传来的轴向压力、水平力、弯矩和扭矩的作用,所以螺栓连接松动后,在塔机上部载荷的作用下标准节的接触面摩擦力逐渐减小直至丧失,机构间出现冲击载荷造成塔身断裂,由此可见,对于塔机标准节螺栓连接松动未及时发现以及预防是很危险的。因此,研究塔机螺栓连接具有重要的意义。
在塔机工作过程中,标准节的螺栓连接是保证被连接结构之间可以可靠的传递力运动。这些都是以标准节的接触面之间具有足够大的预紧力为前提,所以螺栓连接失效的表现方式就是螺栓张紧力的下降。北京理工大学的侯世远 [1] 提出螺栓张紧力决定了螺纹连接松动的机理,预紧力仅仅是螺栓在预紧结束时螺栓所具有的张紧力,并不能用于描述若干循环后的螺纹松动,因此在螺纹联接松动影响因素的研究中应当施加完预紧力之后观察撤掉预紧力之后的螺纹牙应变。
由于很难通过直接观测的方式来了解螺栓松动过程,研究者们往往通过有限元模拟的方法进行研究,但在建模过程中,国内的研究者们往往忽略螺纹的影响,采用简化的手段以近似等效的方式去除螺纹结构,或者通过建立二维模型,来研究螺栓松动机理以及残余预紧力的变化过程。忽略螺纹的方法无法模拟动载荷作用下螺栓联接松动过程,而建立二维模型会使结果的准确性受到一定影响。国外的研究者Junker [2] 、Nassar和Housari [3] [4] 采用有限元模拟与实验相结合的方法,通过建立特定螺栓联接的准确的三维有限元模型,分析研究横向动态载荷下的螺纹牙的应变并且加以实验证明。
基于上述研究,本文中运用了PROE、HYPERMESH以及ABAQUS软件考虑螺纹升角进行了三维建模以及有限元分析,模拟了承载力的分布与Yamamoto解析法进行了比较,并且模拟了横向动态载荷工况下接触对摩擦系数对承载力分布的影响。
2. 螺纹副的建模以及有限元分析
在工程实践中,各类通用的有限元软件可以胜任有限元分析的全过程,但是不同的软件却有不同的长处,为了做到更精确的分析,所以本文中综合运用了3种软件进行了有限元分析。
2.1. 螺纹联接副三维模型的建立
Pro/E是在国内产品设计领域占据重要位置,主要用于特征建模,因此,本文选用Pro/E来建立螺栓联接的三维有限元模型。
QTZ5510型塔式起重机标准节之间采用规格为M33 × 2高强度大六角螺栓与螺母。根据机械设计手册,计算所需三角形螺纹牙型的各参数值如表1所示。
为了减少不必要的计算量,对模型进行了简化处理,将六角螺栓头改为圆形,去掉垫片,连接件改为对称性的,装配后的三维模型如图1所示。
将建立好的螺栓螺母联接件的三维模型保存为“*.iges”格式的文件。再将其导入到HyperMesh中后可以得到效果较好的实体模型,并且没有多余的面和线覆盖在模型上。
2.2. 有限元分析的前处理
在CAE工程技术领域,Hypermesh最著名的特点是它所具有的强大的有限元网格划分前处理功能和后处理功能。使用hypermesh画网格时需要选取网格单元,采用六面体单元进行动态三维有限元仿真可以有效避免四面体网格容易出现体积锁死和过度的抗弯刚度的困难的现象同时可减少网格重划分次数,达到较高的计算精度,故六面体单元是动态三维有限元仿真的首选单元 [5] [6] ,此次六面体网格的单元类型对应于Abaqus中的C3D8R——三维实体缩减积分单元。使用这一单元可以保证位移计算的结果精确可靠,并且在冲击载荷等工况下也能保持稳定性,不会在单元变形时影响到计算结果的精度,并且发生自锁等现象。
对模型进行有限元分析的前处理,包括定义材料属性、划分网格、建立接触面和接触对等。螺栓螺母各部分材料属性选择见表2。
为了提高六面体网格质量,在Hypermesh中进行应当进行适当的实体分割并利用其所提供的solid map网格化分模式,利用Solid map对螺栓和螺母进行六面体网格划分之前,需要对螺栓螺母进行有效分割,再对分割后的各实体部分分别进行六面体网格的划分。
分割后的实体上划分网格以后,得到的螺栓螺母及装配后的三维模型如图2所示。
Table 1. Parameters of thread M33x2
表1. M33x2的螺纹参数
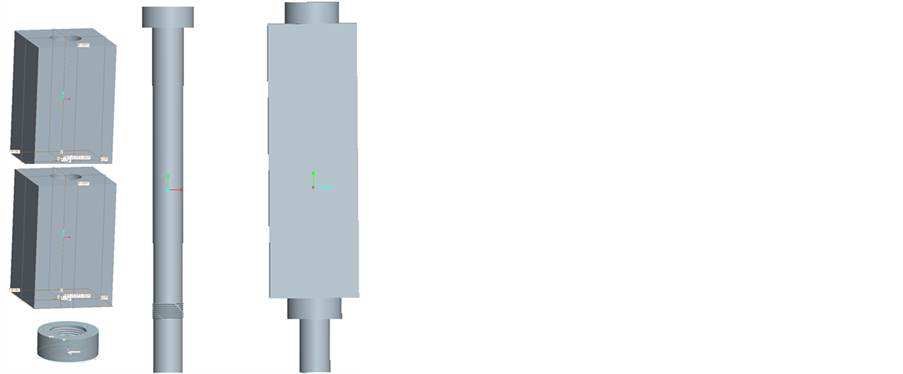
Figure 1. Bolt, nut and the three-dimensional model after assembling
图1. 螺栓螺母及装配后的三维模型
Table 2. Material and properties of bolt, nut and clampers
表2. 螺栓、螺母与夹紧件的材料及属性

Figure 2. Grids of the three-dimensional finite element model of the bolt joint
图2. 螺栓螺母及整体模型的网格划分
2.3. 螺纹连接副的有限元分析及后处理
经过Hypermesh前处理后的三维有限元模型带入Abaqus中进行载荷步的设置以及边界条件的设置,模型的预紧力是采取的直接施加的方式,通过查阅机械设计手册可得出螺栓预紧力计算公式:

 (1-1)
(1-1)
在ABAQUS中选取预紧力的一半最后提交计算,后处理中得到螺栓螺母联接件的等效应力分布云图,如图3所示。
2.4. 螺栓联接有限元模型准确性的验证
Yamamoto法是一种广泛应用的计算螺纹副承载力分布的计算方法,该方法将螺纹牙视为平面应变梁,忽略螺纹升角,根据螺栓螺母体变形协调条件求出在预紧力的作用下螺纹牙根处受力的解析值,依据Yamamoto法 [7] ,螺纹牙的载荷分布可利用下式求得
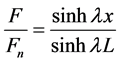 (1-2)
(1-2)
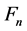 为螺栓受到的轴向力,
为螺栓受到的轴向力,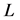 为螺母高度。由式可得到螺栓的合扣部分螺纹截面上的轴向力F的分布,将每层螺纹对应的距离螺母自由端面的位置x代入式中,得到螺栓螺纹各扣截面轴力及轴力系数的解析值。
为螺母高度。由式可得到螺栓的合扣部分螺纹截面上的轴向力F的分布,将每层螺纹对应的距离螺母自由端面的位置x代入式中,得到螺栓螺纹各扣截面轴力及轴力系数的解析值。
通过将模型采取直接施加预紧力方式受到的预紧力作用时螺纹扣部分承载力的分布情况的结果与Yamamoto解析法得到的结果输入到MATLAB中做成曲线图作比较,对模型的准确性进行验证如图4。
从图4中可以看出,靠近螺母接触端面的几扣螺纹拟合结果较为理想,但在螺母自由端的几扣螺纹因为受力变形的影响以及解析法考虑了螺纹升角,所以导致了承载力分布与解析值拟合有偏差。但从总体来说,两种方法得到的螺纹副承载力分布的大体趋势基本趋于一致,前几扣螺纹承受的接触力是最大的,说明采用本文方法模拟螺栓螺母模型的受力情况是正确的,确定了联合建模法的可靠性。
3. 横向动态载荷下塔机螺栓连接中螺纹副摩擦系数的影响
本文在Abaqus中采用有限元的显式动态分析,来施加横向循环载荷激励下,研究不同的螺纹副摩擦

Figure 3. The stress distribution of thread contacting sections
图3. 螺栓螺母以及联接件的等效应力分布云图

Figure 4. Bearing distributions of results and simulated results
图4. 螺栓联接螺纹旋合部分的承载力分布比较图

Figure 5. Force curves reflecting the impact of friction coefficients of thread interfaces
图5. 不同螺纹接触面摩擦系数下螺母螺纹受力变化曲线
系数对承载力分布的影响。
在完成预紧力施加和设置好相应的边界条件之后,对下层夹紧件施加了循环横向激励z模拟动态分析。z的计算公式为:
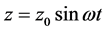 (2-1)
(2-1)
式中: 为激励幅值;
为激励幅值; 为角频率。
为角频率。
在有限元模型上设置各接触面的摩擦因数,分别为螺纹接触面μ,螺栓头与夹紧件的接触面μ1,夹紧件之间的接触面μ2,螺母与夹紧件的接触面μ3。这次施加了200 MPa的预紧力,其中μ1,μ2,μ3保持0.14不变,改变μ的数值,分别取0.1,0.2,0.3进行有限元动态载荷分析,根据图4得出的结论,取了第一层的螺纹接触力数值,并将得出的数值放入MATLAB中作拟合处理,得出结果如下图5。
由图5可以看出,在预紧力的施加完成之后,即0.2 s时,不同的螺纹接触面的摩擦系数下该层螺纹受到的作用力随螺纹面摩擦系数的增大而减小,由此可以看出螺纹接触面的摩擦系数越大,预紧力的施加效果越差。在横向载荷作用的前两个周期中,预紧力作用效果下降最快,但是摩擦系数从0.1增至0.2的时候,残余预紧力增加,而在摩擦系数从0.2增至0.3的时候,残余预紧力却又发生了降低,因此可以看出摩擦系数有一个平稳值,大于和小于这个数值都会导致预紧效果变差。
Hess的研究结果也证明,比较大的摩擦系数会使得在拧紧过程中螺栓螺纹产生更大的弹性扭转变形,在外载的作用下弹性应变能将会释放,释放会导致螺栓产生较大的初始松动,即较大的螺纹接触面摩擦系数对螺栓松动的影响较大 [8] 。
4. 总结
1) 以M33 × 2三角形螺纹的螺栓螺母作为对象用Proe建立三维模型,用Hypermash进行了高质量网格分析,最后用Abaqus进行了分析计算。
2) 将建立的有限元模型所得到的螺纹副承载力与Yamamoto解析法计算得到的螺纹副承载力,进行了对比验证。
3) 在横向动态载荷这一工况下,将螺栓连接模型在不同的摩擦系数下受到的接触力进行了拟合分析,得出 的时候预紧力下降最慢。
的时候预紧力下降最慢。
基金项目
国家自然科学基金项目(51475277),山东省科技发展计划项目(2013GCG20303)。
文章引用
张 烨,王胜春. 塔机螺栓连接有限元建模及动态载荷分析
Finite Element Modeling of Tower Bolt Connection and Dynamic Load Analysis[J]. 机械工程与技术, 2017, 06(02): 91-97. http://dx.doi.org/10.12677/MET.2017.62013
参考文献 (References)
- 1. 侯世远, 廖日东. 螺纹联接松动过程的研究现状与发展趋势[J]. 强度与环境, 2014(2): 39-52.
- 2. Junker, G.H. (1973) Criteria for Self-Loosening of Fasteners under Vibration. Aircraft Engineering & Aerospace Technology, 45, 314-335. https://doi.org/10.1108/eb034981
- 3. Nassar, S.A. and Housari, B.A. (2006) Effect of Thread Pitch on the Self-Loosening of Threaded Fasteners Due to Cyclic Transverse Loads. ASME Journal of Pressure Vessel Technology, 128, 590-598. https://doi.org/10.1115/1.2349572
- 4. Nassar, S.A. and Housari, B.A. (2007) Study of the Effect of Hole Clearance and Thread Fit on the Self-Loosening of Threaded Fasteners. Journal of Mechanical Design, 129, 1053-1062. https://doi.org/10.1115/1.2717227
- 5. Schneiders, R. (1996) A Grid-Based Algorithm for the Generation of Hexahedral Element Meshes. Engineering with Computers, 12, 168-177. https://doi.org/10.1007/BF01198732
- 6. Tekkaya, A.E. and Kavakli, S. (1995) 3-D Simulation of Metal-Forming Processes with Automatic Mesh Generation. Steel Research, 66, 377-383. https://doi.org/10.1002/srin.199501141
- 7. 山本晃. 螺纹联接的理论与计算[M]. 上海: 上海科学技术文献出版社, 1984.
- 8. Sanclemente, J.A. and Hess, D.P. (2007) Parametric Study of Threaded Fastener Loosening Due to Cyclic Transverse Loads. Engineering Failure Analysis, 14, 239-249.
