ABSTRACT

With the introduction of probability and statistics into senior high school mathematics curriculum, whether students can correctly understand the concept of probability and statistics, and comprehend the random thought, statistical thought and probabilistic thinking, largely depends on teachers’ understanding of probability and statistics. As a future mathematics teacher, mathematics normal students’ cognitive level of probability and statistics obviously has an important impact on mathematics teaching in senior high school. The purpose of this paper is to explore the cognitive level of mathematics normal students’ high school probability core knowledge. Through investigation, it is found that the mathematics normal students’ cognitive level of probability is not optimistic, which should be paid attention in the cultivation of mathematics normal students in the future.

Keywords:Mathematics Normal Students, Probability and Statistics, Cognitive Level

数学师范生对高中概率核心知识认知水平的调查研究

刘芳

赣南师范大学数学与计算机科学学院，江西 赣州

收稿日期：2019年4月19日；录用日期：2019年5月2日；发布日期：2019年5月9日

摘 要

随着概率统计内容引入高中数学课程，学生能否正确理解概率统计概念、领会随机思想、统计思想和概率思维方式，很大程度上取决于教师对概率统计的理解。而作为未来数学教师的数学师范生对概率统计知识的认知水平显然对高中数学教学有着重要影响。本文旨在探讨数学师范生对高中概率核心知识的认知水平，通过调查发现数学师范生对概率知识的理解水平不容乐观，这是要在今后的师范生培养中给予关注的。

关键词 :数学师范生，概率统计，认知水平

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

2003年5月出台的《普通高中数学课程标准(实验稿)》 [1] (以下简称《课标》)明确地将概率与统计作为高中数学课程的必修内容，并将数据处理、统计知识等纳入数学“双基”。这一《课标》于2004年开始实施，经过十多年的努力，高中数学教师理应已经具备全面而系统的概率统计知识，能够深刻理解随机思想、统计思想和概率意义。但据李勇等 [2] 2016年做的调查研究显示高中数学教师特别是青年教师对《课标》涉及的概率统计知识的认知水平不容乐观。造成这一现象的原因是多方面的，而关于数学师范生的培养是其中的一个重要原因。

概率是“不确定数学”，其研究目的是寻找随机现象中的规律性。它与代数、几何在思维方式和学习方式上有很多不同，故而相应的教学方法、教学策略、课堂设计以及学生的学习方式也应随之变化。然而，在目前的高等师范教育中，《概率论与数理统计》虽然一直是数学专业的必修课程，但是对数学师范生关于概率知识的学习并没有特别的要求，教材也没有随着高中新课标的出台而调整。这就造成了我们延用旧的方法、策略和方式培养新课标下数学师范生的随机思想、统计思想和概率思维方式的现状，使得作为未来担负起中小学数学教学工作储备军的数学师范生不能很好地适应新课标下概率的教学。如何改变这种现状，提高数学师范生的教育质量呢？我们认为，任何方法的有效实施都应该以数学师范生对概率知识的掌握情况为基础。那么，作为未来数学教师的数学师范生对概率知识的认知处于何种水平？是否存在诸多不足？如何克服这些不足，提升理解水平？这些问题的调查研究，可以为数学师范生的培养提供参考。

2. 调查问卷的设计

本研究的目的是分析数学师范生对概率核心知识的认知水平现状，得出数学师范生概率学习的认知框架，并分析、研究学生在概率学习中存在的主要问题，为改进课程教学和提高数学师范生培养质量提供依据。因此，问卷中的问题涉及的知识以《课标》要求的概率内容为范围。

在高中新课标教材中概率统计内容出现在必修3 [3] 与选修2~3 [4] ，其中概率部分主要由随机事件与概率、古典概型与几何概型、概率应用、条件概率与事件的独立性、随机变量的数字特征五部分构成。

通常，调查问卷可由解答题和选择题构成，这两类题目各有利弊，解答题的作答往往费时较多，容易引起调查对象的反感，影响调查结果，但如果被试对象配合认真作答的话，可以获得更多的信息。而选择题容易确定标准答案，可以减少被试对象的作答时间和作答误差，也便于统计分析。对概率知识认知的调查采用“选择题 + 解答题”的形式构成测试问卷，被试对象在选择正确答案的同时还需要写出作答理由。我们从李俊所著《中小学概率的教与学》 [5] 附录测试题中选取I1(2)、I2(1)、I4(5)、II1(8)、II2(3)、II3(4)、III1(1)、IV8分别为调查问卷的第1题至第8题。

3. 结果与分析

本研究的调查对象是江西省赣州市某师范大学2016级数学与应用数学(师范类)专业的本科生，调查时间安排在调查对象完成《概率论》课程学习后两周，答题时间为40分钟，共计发放169份测试问卷，最终回收问卷165份，其中有效问卷155份，有效率93.9%。有效问卷是指学生在规定时间内至少完成80%的题目，没有作答或所有题都没有给出解答理由的问卷视为无效试卷。

我们的主要目的是了解数学师范生对现行高中数学教材中的概率知识的解释能力，为此我们将有效问卷中每道测试题的作答结果分成四类，即错误–模糊–理解–掌握：

1) 错误：题目没有作答，或选择答案错误；

2) 模糊：选择答案正确，但没有给出选择理由或者所述理由完全与题意无关；

3) 理解：选择答案正确并给出了选择理由，但所述理由不充分、有部分错误；

4) 掌握：选择答案正确且所述理由完全正确。

分别统计每道题各类作答结果的人数，再计算出其频率，画出相应的频率直方图(图1、图2)。下面我们逐个给出调查的结果和分析。

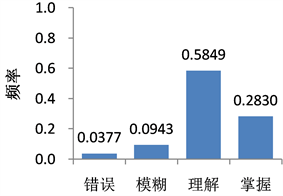
Histogram 1. Probability questionnaire question 1

直方图1. 概率问卷第1题

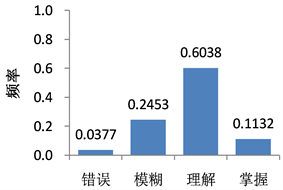
Histogram 2. Probability questionnaire question 2

直方图2. 概率问卷第2题

1) 第1~3题用于考察学生是否能正确区分不可能事件、可能事件和必然事件，正确答案分别为C、B和B。样本空间、样本点和随机事件是概率论中最基本的概念，是引入概率定义所必须的术语。随机事件根据其包含样本点的多少分为不可能事件、可能事件和必然事件。按照《课标》的要求，学生应该能根据实例所示的随机现象写出样本空间，并把所求的随机事件用集合形式表示。直方图1~直方图3说明，超过70%的学生能够正确区分不可能事件、可能事件和必然事件，属于错误和模糊理解的比例不到30%。对模糊理解问卷的访谈分析，发现部分学生对问卷中的问题背景不清楚，导致答题正确而没有说明选择理由。总体上，数学师范生对概率论中的样本空间、随机事件的理解状况较好，但与高中教学要求仍有差距。

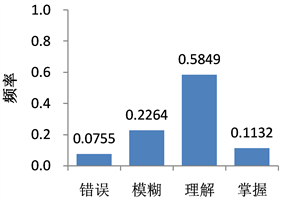
Histogram 3. Probability questionnaire question 3

直方图3. 概率问卷第3题

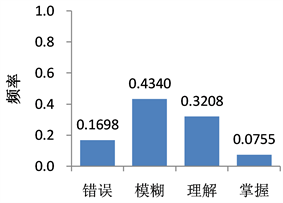
Histogram 4. Probability questionnaire question 4

直方图4. 概率问卷第4题

2) 第4题和第5题用于考察学生对大数定律的理解深度，正确答案分别为E和C。大数定律有多种形式，其中最简单的伯努利大数定律解释了“概率是频率的稳定值”，因此可以用频率的稳定值去获得概率(即为概率的统计定义)。对概率的统计定义需要注意两点：一是频率在其概率附件摆动；二是重复试验次数越大，频率越接近概率。直方图4和直方图5说明，对大数定律的理解，属于理解和掌握水平的学生比例不到40%，而属于模糊理解水平的学生比例为43.40%。总体上，数学师范生对大数定律的理解深度不理想。

3) 第6题用于考察学生使用预言结果的倾向以及从频率的角度解释概率的能力。根据Konold [5] 的描述，使用预言结果法的学生往往以某一事件发生概率是大于还是小于50%作为预言该结果是否发生的标准。例如：若是你预言某一事件发生的概率很大，而它又真的发生了，那么他们会认为你的预言很准，如果没有发生，他们则会认为你的预言很不准。直方图6说明，属于模糊和理解水平的学生比例各占9.43%，而错误理解的比例高达81.13%。总体上，大多数数学师范生会使用预言结果法，缺乏从频率角度解释概率的能力，他们的理解水平与高中教学要求有很大差距。

Histogram 5. Probability questionnaire question 5

直方图5. 概率问卷第5题

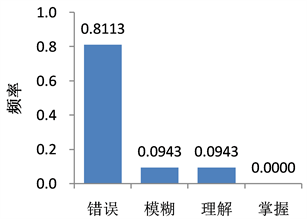
Histogram 6. Probability questionnaire question 6

直方图6. 概率问卷第6题

4) 第7题用于考察学生对古典概型的理解水平，正确答案是A。古典概型是《课标》要求的基本内容，也是高中概率统计教学的重点内容。直方图7说明，超过96%的学生能答题正确，其中属于理解和掌握水平的学生比例分别为52.83%和33.96%。总体上，数学师范生对古典概型的理解状况比较好。

Histogram 7. Probability questionnaire question 7

直方图7. 概率问卷第7题

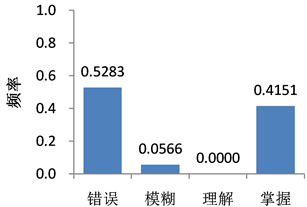
Histogram 8. Probability questionnaire question 8

直方图8. 概率问卷第8题

5) 第8题用于考察学生对随机向量和独立性的认识深度，正确答案是C。我们可以用两个相互独立的随机变量刻画旋转两个转盘的指针所得的结果，然后用随机变量的分布律来计算随机事件的概率。直方图8说明，52.83%的学生计算错误，41.51%的学生能给出完整的计算过程，而5.66%的学生属于模糊理解水平。总体上，数学师范生对随机向量和独立性的理解深度不理想，缺乏利用所学知识解释实际问题的能力。

4. 结论与讨论

调查结果表明，地方性师范院校的数学师范生对概率核心知识的认知水平不容乐观，部分数学师范生对某些概率核心知识的理解水平都处于错误或模糊状态，理解深度不够，缺乏用这些概念答疑解惑的能力，将来不能很好地承担高中数学概率知识的教学任务。

根据本次的调查研究和平时了解的情况，对造成数学师范生概率核心知识认识不理想的现状归因如下：

首先，大学的教学改革滞后于高中的教学改革，造成大学教学与高中教学的脱节。新《课标》自2003年颁布以来，经过十多年的改革，高中教学在教学方法、课程理念、课程框架和教学内容上都发生了巨大的变化。高等教育关于教学的改革进展缓慢，虽然近年来教育部在推进师范专业的培养方式改革，但是已经明显滞后于高中的教学改革。同时，高校和高中的教学改革缺乏有效的沟通和交流，基本上是独立进行，这就造成了大学数学与高中数学在教学内容、教学方式和教学理念等方面的脱节。例如：高中概率概念的教学中高中教师一般会创造问题情境，鼓励学生用真实的活动、真实的数据和直观模拟试验去检查、修改或改正他们对概率概念的错误认识，并且学会分析和发现错误认识的原因，采取探究式的学习策略学习概率概念知识；而大学教师常常也不太愿意让这样的“小孩子游戏”占用太多的教学时间。

其次，大学的概率课程与高中的教学需求脱节，造成数学师范生无法适应高中概率的教学。相比较大学的教学，高中概率的教学更注重通过具体实例或实验，让学生学习如何收集和整理数据，如何用图表直观表示数据，如何刻画数据的数字特征等方法；让学生在具体实例的操作、解答过程中，感悟根据实际情况进行科学决策的必要性和可能性，体会随机性思维与确定性思维的差异、归纳推断与演绎证明的差异，积累数据分析的经验。显然，数学师范生在大学中缺乏这方面的训练。

第三，数学师范生对概率的学习方式也存在诸多问题。有些数学师范生认为概率的学习与数学的学习没有区别，只要会做题解题就可以了，忽略了运用概率知识分析、解释实际问题的能力训练。有些数学师范生学习缺乏主动性，“考什么就学什么”，不重视结合概率的特点系统学习相关知识。还有些数学师范生不重视教学技能的学习，自然没有考虑怎样教学才能体现概率的特点，才能有利于学生数据分析素养的形成。

为了进一步提高数学师范生对概率知识的认知水平，针对以上的原因，提出以下几点建议：

1) 高等师范院校应紧随高中数学课程改革，对概率的教学进行改革，改善师范生所学与高中教学要求脱节的现状。例如在数学史的教学中增加概率的发展史，通过对数学发展史和概率发展史对比学习，不但能开阔师范生的数学视野，也能激发师范生学习概率和统计的兴趣，进而重视概率的学习。高中概率和统计的教学除了概念和方法的学习外，比较注重实践教学，强调运用概率方法解决实际问题的能力训练。在大学概率课程的教学中，可以加强信息技术手段的应用，在某些内容(如蒲丰投针试验、蒙特卡罗等)的教学中增加Excel统计工具的演示，使数学师范生对这些方法有了直观的认知，缓解理论学习的枯燥感，提高教学效果。

2) 加强大学概率论课程的改革。当前主流的概率论教材与高中教学要求有些脱节。高等师范院校可以根据数学师范生的专业特色，编写合适的概率论教材或辅助书籍，以满足高中概率的教学要求。另外，增设概率实验教学课，改变现在概率论课程只有理论课没有实验课的现状，数学师范生利用计算机通过数学软件验证学到的概率方法，有利于他们理解概率思想，培养了他们分析问题和解决问题的能力。

3) 加强数学师范生对概率思想的重视。在应试教育背景下，师范生对概率的学习侧重于解题技巧训练，忽略了运用概率思想分析、解释实际问题的能力训练。高师院校可以在概率论课程后布置一些调查研究任务，让师范生参与数据收集和数据分析的全过程，使师范生在调查过程中运用概率的思想方法，解决具体问题，让他们学有所用，获得学习的满足感。

受诸多客观条件的限制，本次调查只在江西省一所师范院校进行，所调查的结果具有一定的局限性和片面性，不能全面地反映我国数学师范生对概率核心知识的认知水平。但是从调查结果也能发现数学师范生对概率知识的理解水平不容乐观，与理想状态存在一定差异，这是要在今后的高等教育教学改革中给予关注的。

基金项目

江西省研究生创新专项资金项目：YC2017-S396；江西省教育厅教学改革项目：JXJG-16-14-10；校教学改革项目：150721。

文章引用

刘 芳. 数学师范生对高中概率核心知识认知水平的调查研究
Research on the Cognitive Level of Mathematics Normal Students’ High School Probability Core Knowledge[J]. 社会科学前沿, 2019, 08(05): 689-695. https://doi.org/10.12677/ASS.2019.85097

参考文献