1School of Electrical Engineer, Southeast University, Nanjing Jiangsu
2State Grid Jiangxi Power Company Institute, Nanchang Jiangxi
3Nanjing Guodian Nanzi Power Grid Automation Co. Ltd., Nanjing Jiangsu
4College of Energy and Electrical Engineering, Hohai University, Nanjing Jiangsu

Received: Dec. 1st, 2017; accepted: Dec. 16th, 2017; published: Dec. 26th, 2017

ABSTRACT
For the power grid with large-scale wind power integration, using the probabilistic power flow calculation and the concept of entropy, a ranking indicator based on the available capacity entropy of branch and sorting method under multi-scenarios for expected contingency are proposed in order to speed up the probabilistic static security analysis and the impact of branch outage on the system can be described in the view of branch available capacity. The simulation is verified in IEEE-118 system and the results indicate that the proposed method can evaluate power system static security precisely and find the weakness of power system. Meanwhile, it greatly shortens the time and provides reference information for electric power operation personnel.
Keywords:Entropy of Branch Available Capacity, Probabilistic Power Flow, Static Security Analysis, Expected Contingency Sorting
基于支路可用容量熵的概率静态安全分析
喻洁1,孙旻2,李鹏3,曾伟2,杨塞特4
1东南大学电气工程学院,江苏 南京
2国网江西省电力公司电力科学研究院,江西 南昌
3南京国电南自电网自动化有限公司,江苏 南京
4河海大学能源与电气学院,江苏 南京
收稿日期:2017年11月1日;录用日期:2017年12月16日;发布日期:2017年12月26日

摘 要
针对接有大规模风电的电网,结合概率潮流计算,引入熵的概念,从支路可用容量的角度来描述不同支路开断后对系统造成的影响,提出了一种基于支路可用容量熵的预想事故排序指标和基于多场景下的预想事故排序方法,进而提高系统静态安全分析速度。通过IEEE-118节点系统进行仿真计算,结果表明该方法能准确地发现系统潜在的薄弱环节,并大大缩短了静态安全分析时间,为电力运行人员提供可参考的信息。
关键词 :支路可用容量熵,概率潮流,静态安全分析,预想事故排序

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
预想事故排序作为电力系统静态安全分析中的一个重要部分 [1] [2] [3] ,其目的是准确而快速地找到那些对系统造成较大影响的危险事故,并按照其严重程度进行排序,从而着重对其进行详细分析,可以大大降低计算量 [4] [5] [6] 。文献 [7] 所选用的预想事故排序指标同时体现了经济性和风险性,但是其通过确定潮流计算,无法精确适用于大规模风电接入的系统。文献 [8] 将电力网络拓扑与系统潮流相结合,分别用介数反映元件在网络拓扑中的重要程度,用线路功率反映线路负载程度。文献 [9] 通过节点电压等电气量得出支路指标,并基于支路指标的变化的到事故严重程度指标。传统的潮流分析计算是在所有给定量都是确定的基础上进行的,据此计算出的各节点电压及各支路潮流也都是确定值,但是实际的电力系统中负荷预测的误差以及运行条件的不断变化等情况都会使得电力系统具有不确定性,而随着电力系统规模的不断扩大,这种不确定性更加明显。这就需要用概率理论来描述这种不确定性,探索相应的数学建模、计算机算法和实际应用,称为概率潮流研究。而上述文献均只适用于确定潮流计算,并不能很好地应用于概率潮流计算。为此,本文将结合概率潮流计算结果,提出一种基于支路可用容量熵的预想事故排序指标和基于多场景下的预想事故排序方法,加快静态安全分析速度。在IEEE-118节点系统上进行算例分析,验证了该方法的有效性。
2. 基于支路可用容量熵的排序指标
熵理论在19世纪50年代由Clausius提出 [10] [11] [12] [13] ,最先被应用到热力学领域,来表征系统状态量的混乱程度,它反映了一种自然界现象有序程度演化的规律,被广泛应用于其他学科。
当系统存在多种状态 ,且每种状态存在的概率为 时,系统的熵定义为:
(1)
式中: 为常数; 为系统状态总数。
在稳定状态下,电力系统每条支路的负载率均衡,因此支路可用容量率基本相同,可以理解为支路可用容量率分布均匀有序,系统安全性较高;当开断系统内的某一条支路,必会增加附近其他几条支路上的有功功率,进而导致其可用容量率变小,使某些支路处于重载甚至过载状态,系统安全性较低。根据上述特点,本文提出了一种基于支路可用容量熵的预想事故排序指标,其中支路可用容量率表示为:
(2)
式中: 为支路 的传输容量; 为开断支路 后支路 有功功率的期望值。
对式(2)进行归一化处理得:
(3)
式中: 为支路总数。
由式(3)得到支路 的可用容量熵为:
(4)
定义基于支路可用容量熵的预想事故集排序指标为:
(5)
式中: 为基态下支路 的有功功率的期望值。
本文提出的基于支路可用容量熵的预想事故排序指标的特点如下:
1) 支路 基态下有功功率的期望值 越大,开断该支路后其有功向附近其他支路进行转移对其他支路有功的影响越大;
2) 开断支路 后得到的支路可用容量熵 越小,支路 的有功转移分布越聚集在少数部分的几条支路上,使得部分支路可用容量率很小,处于重载甚至过载状态,越限概率很高。
因此支路 的预想事故集排序指标 越大,反映出开断支路 对系统造成的影响越大、后果越严重,系统安全性也就越低。
3. 基于多场景下的排序方法
在对系统进行N-1校验之前,如果可以先对预想的事故进行排序,有选择性的分析那些开断后对系统造成影响比较严重的支路,那么可以显著地减少计算量,提高分析速度 [14] [15] [16] 。本文提出的预想事故排序方法主要是基于多场景下的直流概率潮流结果快速计算出所有预想事故的排序指标,根据对系统造成后果严重性进行排序,具体步骤如下:
1) 利用拉丁超立方抽样抽取每个风电场输出功率的样本值,数量为N,即场景数。
2) 根据风电场出力的样本值,在每一个场景下计算系统内各支路基态下的有功功率,并对所有支路一一进行开断,通过直流潮流计算出除开断支路以外所有支路的有功功率,直至所有场景下所有支路都完成了潮流计算。
3) 根据得到的潮流结果计算出所有预想事故基于支路可用容量熵的排序指标,对系统造成的影响程度由大到小进行排列,得到预想事故一览表。
本文提出的基于多场景下的预想事故排序方法流程如图1所示。
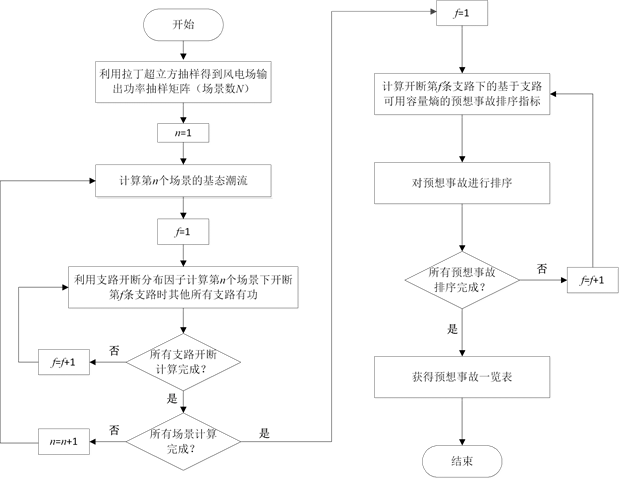
Figure 1. Flow chart of contingency accident sequencing method, based on multiple scenes
图1. 基于多场景下的预想事故排序方法流程图
4. 基于支路可用容量熵的概率静态安全分析
完成所有预想事故的排序后,按照预想事故一览表中顺序逐个进行交流概率潮流计算分析,得到反映整个系统静态安全性的概率评价指标。由于排序结果可能会出现一定的误差,存在蒙蔽现象,即一个引起多个线路出现重载但并未过载的预想事故,其排序指标反而高于只有个别产生过负载的预想事故的指标,从而引起了排队的错误,漏掉了对有意义预想事故的分析。因此在进行交流潮流校验过程中连续几个预想事故都未引起其他支路过负荷的情况下才终止分析。
基于概率潮流的电力系统静态安全分析的具体步骤如下:
1) 对系统内所有支路依次进行开断进行直流概率潮流分析,根据预想事故排序指标快速得到预想事故一览表;
2) 根据表中的预想事故顺序,依次进行交流概率潮流分析,计算支路有功功率的期望、方差、越限概率和概率分布等结果,进一步获得电力系统静态安全概率评价指标;
3) 如果满足终止判据则跳出循环,即连续校验5个预想事故均不引起系统内其他支路有功功率越限,否则转至步骤2)。
基于概率潮流的电力系统静态安全分析方法流程如图2所示。
5. 算例分析
采用IEEE-118节点系统进行仿真分析,将9个风电场分别接入40号、42号、46号、49号、66号、76号、77号、80号和116号节点上,风电出力累积分布函数均服从正态分布,期望值为100 MW,标准差为20 MW。
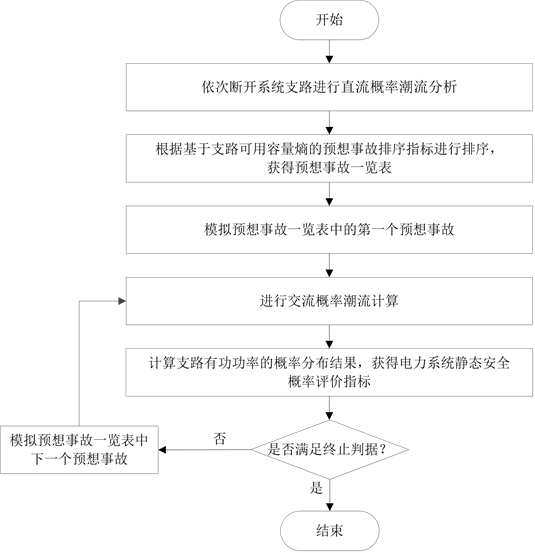
Figure 2. Flow chart of static security analysis, based on probabilistic load flow
图2. 基于概率潮流的静态安全分析流程图
通过直流潮流法计算基于支路可用容量熵的预想事故排序指标 ,按照指标由大到小进行排序,得到预想事故一览表,排在前20位的计算结果如表1所示。
按表1的顺序进行交流概率潮流计算校验,所选用的静态安全概率评价指标
,其中 为开断支路 后,支路 的有功功率 [11] 。阈值设为0.001,即当
时,认为该事故不会引起系统过负荷。其中,阈值的设定基于系统结构以及系统状态的变化。经过大量实验数据的校验,将阈值设置为0.001时,据此阈值判断出的事故情况最符合实际系统发生事故时的情况。开断预想事故的静态安全概率评价指标计算结果如表2所示。
其中开断支路8-9、85-86、68-116时,交流概率潮流计算不收敛,说明在当前运行方式下,系统潮流严重畸形。所以支路8-9、85-86、68-116为关键支路,加强对其监测、控制和保护,使其运行在安全稳定的范围内。
选取其中开断后对系统影响较大的支路65-68进行分析,开断支路65-68时其他部分支路越限概率如表3所示。
结合具体的网络结构,对开断支路65-68引起系统潮流变化的原因进行详细分析,支路65-68附近的网络结构图如图3所示,且标注支路有功功率流向。以支路68-81和64-65为例,这两条支路有功功率在开断支路65-68前后累积分布曲线的变化情况分别如图4和图5所示。
Table 1. Schedule of contingency accident
表1. 预想事故一览表
Table 2. Evaluation index of the static security probability
表2. 静态安全概率评价指标
Table 3. Limit violation probability of some lines
表3. 其他部分支路越限概率
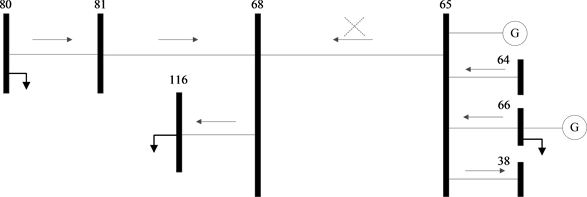
Figure 3. Network structure diagram near line 65-68
图3. 支路65-68附近网络结构图
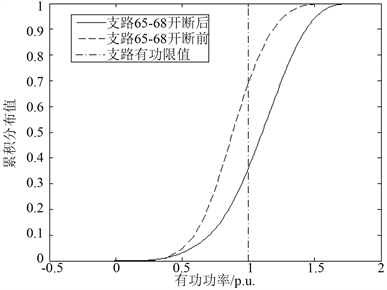
Figure 4. Active power cumulative distribution curve of line 68-81 before and after line 65-69 outage
图4. 支路65-68开断前后支路68-81有功功率累积分布曲线
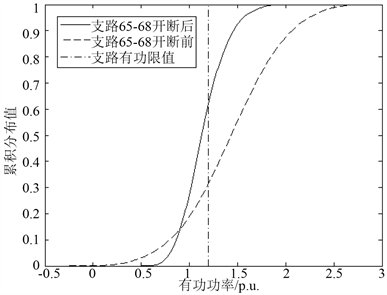
Figure 5. Active power cumulative distribution curve of line 64-65 before and after line 65-68 outage
图5. 支路65-68开断前后支路64-65有功功率累积分布曲线
由图4可知,支路65-68断开后,支路68-81的有功功率期望值增大,由0.8856 p.u.增加到1.0847 p.u.,该支路有功功率大于1 p.u.的概率(即越限概率)由30.9278%增加到63.9692%。这是因为支路65-68断开后,原本节点116上的负荷由来自支路65-68和68-81共同提供,现在仅由支路68-81独自承担。在这种情况下,为了保证系统安全可靠的运行,短期内可以通过切除节点116上的部分负荷来限制支路的越限情况,长期有效的方法可以是在节点116或节点68上增加发电机组,就近供电,为了降低该支路越限概率还可以增加支路传输容量。
由图5可知,支路65-68断开后,支路64-65的有功功率期望值减小,由1.4308 p.u.减小到1.1466 p.u.,该支路有功功率大于1.2 p.u.的概率(即越限概率)由68.2607%减小到37.6498%。这是因为支路65-68断开后,节点65和节点66上发电机输出功率和支路64-65上的有功功率不再流向支路 65-68,只通过支路38-65向外流出,对有功的需求降低,也可以通过增加支路传输容量来降低支路的越限概率。
根据预想事故一览表,继续进行交流概率潮流分析,发现当开断支路37-39时静态安全概率评价指标为0.0007,小于阈值0.001,即可认定系统未出现过负荷情况。连续开断支路45-46、17-31、46-47和76-118,系统的静态安全概率评价指标均小于阈值,因此对之后的14条支路不需要继续进行开断分析,这样减少了7.5269%的工作量。经计算,预想事故排序的时间为2.378 s,按照预想事故一览表中预想事故的顺序逐一验证到第172条支路所需时间为677.137 s,即本文所提出的电力系统静态安全分析时间为679.515 s,而对电力系统进行完整交流潮流分析所需时间为736.810 s,可以看出本文所提出基于概率潮流的电力系统静态安全分析方法可以节约大量的计算时间。
6. 结束语
结合概率潮流计算,本文提出一种适用于分析大规模风电并网的静态安全分析方法。同时提出的基于支路可用容量熵的预想事故排序指标和基于多场景下的排序方法可以对预想事故快速排序,大大降低了静态安全分析的计算量。算例表明该方法的有效性和工程实用价值,并结合网络拓扑,分析系统潮流变化情况,给出相应的改善措施。
致谢
本文由国网江西电力公司电力科学研究院“面向能源互联网的区域电网低碳电力调度技术研究”项目和南京国电南自电网自动化有限公司“电力市场仿真交易平台设计服务”项目资助。
文章引用
喻 洁,孙旻,李鹏,曾伟,杨塞特. 基于支路可用容量熵的概率静态安全分析
Probabilistic Static Security Analysis Based on Entropy of Branch Available Capacity[J]. 输配电工程与技术, 2017, 06(04): 55-63. http://dx.doi.org/
参考文献 (References)
- 1. 留毅, 章静芳. 电力系统静态安全分析综述[J]. 科技创新导报, 2010(30): 64-64.
- 2. 朱星阳, 黄宇峰, 张建华, 等. 基于随机潮流的含风电电力系统静态安全评估[J]. 电力系统自动化, 2014, 38(20): 46-53.
- 3. 傅旭. 考虑不确定因素的电力系统静态安全预防控制[J]. 电力自动化设备, 2014, 34(2): 120-124.
- 4. 张志坚, 乔振宇, 王建东, 等. 预想事故排序算法比较[J]. 电力自动化设备, 2001, 21(11): 25-27.
- 5. 马平, 蔡兴国. 电压稳定分析中支路型故障筛选及排序算法研究[J]. 中国电机工程学报, 2007, 27(1): 44-48.
- 6. 邱晓燕, 李兴源, 林伟. 在线电压稳定性评估中事故筛选和排序方法的研究[J]. 中国电机工程学报, 2004, 24(9): 50-55.
- 7. 王永辉, 王克文, 刘畅, 等. 概率潮流在电力系统静态N-1校验中的应用[J]. 计算机仿真, 2013, 30(2): 125-129.
- 8. 陈波, 郭勇, 施世鸿, 等. 一种预想事故自动选择的新方法[J]. 陕西电力, 2009, 37(5): 10-14.
- 9. 倪涌炯, 方鸽飞, 叶剑锋. 基于电压稳定的在线预想事故筛选和排序[J]. 电工技术, 2006(2): 31-32.
- 10. 苟竞, 刘俊勇, 刘友波, 等. 基于能量熵测度的电力系统连锁故障风险辨识[J]. 电网技术, 2013, 37(10): 2754-2761.
- 11. 李勇, 刘俊勇, 刘晓宇, 等. 基于潮流熵的电网连锁故障传播元件的脆弱性评估[J]. 电力系统自动化, 2012, 36(19): 11-16.
- 12. 曹娟, 张颖淳, 苏伯洪. 基于流量熵的道路交通网络脆弱性优化[J]. 西南师范大学学报(自然科学版), 2014(7): 30-35.
- 13. 刘文颖, 王佳明, 谢昶, 等. 基于脆性风险熵的复杂电网连锁故障脆性源辨识模型[J]. 中国电机工程学报, 2012, 32(31): 142-149.
- 14. 杜正旺, 哈恒旭, 宋扬, 等. 基于灵敏度–补偿法的电力网络开断潮流新算法[J]. 电力系统保护与控制, 2010, 38(16): 103-107.
- 15. 刘怡芳, 张步涵, 李俊芳, 等. 考虑电网静态安全风险的随机潮流计算[J]. 中国电机工程学报, 2011(1): 59-64.
- 16. 蒋平, 杨绍进, 霍雨翀. 考虑风电场出力随机性的电网静态安全分析[J]. 电力系统自动化, 2013, 37(22): 35-40.
