Statistics and Application
Vol.06 No.02(2017), Article ID:20486,8
pages
10.12677/SA.2017.62013
The Recursive Credibility Model of Maximum Entropy Method
Xinghong Zhang*, Lijun Wu#
College of Mathematics and System Sciences, Xinjiang University, Urumqi Xinjiang
*第一作者。
#通讯作者。

Received: Apr. 2nd, 2017; accepted: Apr. 25th, 2017; published: Apr. 28th, 2017

ABSTRACT
This paper is devoted to study the credibility estimate of risk premium with maximum entropy method. Combined with maximum entropy method, in a recursive credibility model, on the basis of Principles of minimum the mean squared error and maximum entropy, we get the expression for credibility estimate, which generalizes the classical credibility theory.
Keywords:Maximum Entropy, Recursive Credibility Model, Credibility Factor
最大熵方法下的递推信度模型
张兴红*,吴黎军#
新疆大学数学与系统科学学院,新疆 乌鲁木齐

收稿日期:2017年4月2日;录用日期:2017年4月25日;发布日期:2017年4月28日

摘 要
文章研究了最大熵方法下的风险保费的信度估计问题,即在递推信度模型中,结合最大熵方法,根据均方误差最小原则和熵最大原则得到了信度估计的表达形式,推广了经典的信度理论。
关键词 :最大熵,递推信度模型,信度因子

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
精算师对保险产品制定合理价格的过程叫做保费定价,在对保费定价时,保险公司关注的问题是:怎样使征收的保费足够理赔且产品具有竞争力。精算师在对保险产品定价时,必须用科学的方法对保险产品进行分析和评价,以使得制定的保费价格具有合理性,既能满足保险公司的正常赔付,又能给公司带来一定利润,如果征收的保费太高,那么投保人数会减少,如果过低,那么保费不够理赔,给公司带来损失,因此保险公司最关心的重要问题之一就是保费的定价。
信度理论就是研究如何根据历史索赔额来解决保险费率的合理制定问题,在非寿险精算和保险实务中对下个时期的保费定价具有重要意义,文献 [1] 给出了不需要考虑分布的经Buhlmann信度模型,但是Buhlmann模型对各个年份的索赔额赋予了同样的权重。显然,对于实际问题,不同的索赔额有各自的权重似乎更为合理。文献 [2] 给出递推信度模型即n + 1年的线性信度保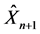 是第n年的索赔额
是第n年的索赔额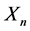 ,第n年的线性信度保费
,第n年的线性信度保费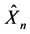 的加权和,文献 [3] 在Buhlmann模型的基础上也得到了具有递推形式的信度模型。文献 [4] 依据期望和协方差的重要性质进一步推广了递推信度模型。胡莹莹在文献 [5] 中得到了指数保费原理下的递推信度模型,并证明了年份较近的索赔额具有较大的权重。文献 [6] 给出了用最大熵方法定量求解问题的一般技术途径,文献 [7] 给出类似最大熵方法的最小交叉熵方法并确定了权重,文献 [8] 用最大熵方法估计了离散指数族里尺度参数的分布,并估计了信度因子,文献 [9] 用最大熵方法计算了近似Bayes估计,文献 [10] 得到了最大熵方法下的纯稳健信度估计。
的加权和,文献 [3] 在Buhlmann模型的基础上也得到了具有递推形式的信度模型。文献 [4] 依据期望和协方差的重要性质进一步推广了递推信度模型。胡莹莹在文献 [5] 中得到了指数保费原理下的递推信度模型,并证明了年份较近的索赔额具有较大的权重。文献 [6] 给出了用最大熵方法定量求解问题的一般技术途径,文献 [7] 给出类似最大熵方法的最小交叉熵方法并确定了权重,文献 [8] 用最大熵方法估计了离散指数族里尺度参数的分布,并估计了信度因子,文献 [9] 用最大熵方法计算了近似Bayes估计,文献 [10] 得到了最大熵方法下的纯稳健信度估计。
本文将在递推信度模型的基础上结合最大熵方法得到未来保费的递推形式,并用数值模拟验证定理的结果。
2. 模型假设与准备
定义1
线性信度保费具有递推模型,如果存在序列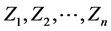 使得
使得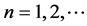
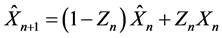 其中
其中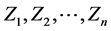 是n年历史索赔额,
是n年历史索赔额,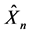 是第n年线性信度保费的预测值。
是第n年线性信度保费的预测值。
定义2
熵是随机变量不确定度的度量,设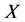 是一个离散型随机变量,概率取值空间为
是一个离散型随机变量,概率取值空间为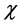 ,概率函数为
,概率函数为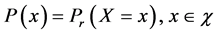 ,则
,则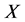 的熵为
的熵为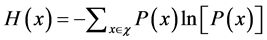 ,其中
,其中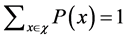 。
。
最大熵原理的主要思想是:在只掌握关于未知分布的部分知识时,应该选择符合这些知识但熵值最大的概率分布。在给定约束条件下,由最大熵原理求解最优解问题通常由拉格朗日乘子法来确定本节研究满足如下假设的信度模型:
假设1
令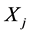 表示保单合同第j年的索赔数据
表示保单合同第j年的索赔数据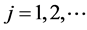 其中
其中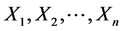 是由风险参数
是由风险参数 决定的,
决定的,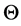 的先验分布是
的先验分布是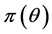 ,且有
,且有
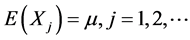 (2.1)
(2.1)
假设2
给定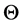 ,
,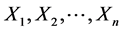 是相互独立的,且有
是相互独立的,且有
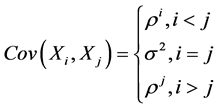 (2.2)
(2.2)
其中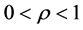 。
。
3. 主要结果证明
引理1 假设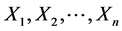 是n年历史索赔额数据,若未来保费具有线性形式
是n年历史索赔额数据,若未来保费具有线性形式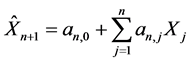 ,其中
,其中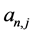 是第j年索赔额的权重,
是第j年索赔额的权重,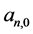 是常数,则在假设1和假设2条件下的最小二乘估计式有如下形式:
是常数,则在假设1和假设2条件下的最小二乘估计式有如下形式:
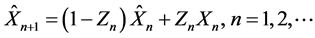 其中
其中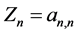 。
。
引理1的证明
首先求解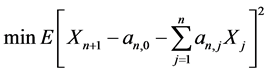
令
 (3.1)
(3.1)
对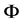 关于
关于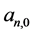 求导并令导数为0得
求导并令导数为0得
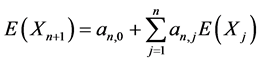 (3.2)
(3.2)
对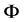 关于
关于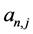 求导并令导数为0得
求导并令导数为0得
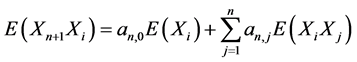 (3.3)
(3.3)
由(3.2)式两边乘以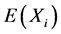 减去(3.3)式得
减去(3.3)式得
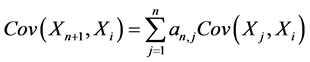 (3.4)
(3.4)
由(3.4)式得
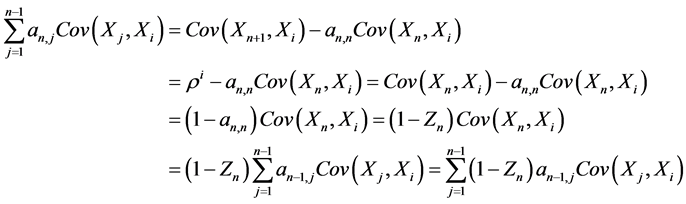
所以
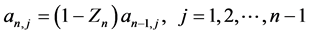 (3.5)
(3.5)
当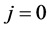 时,由(3.2)式得
时,由(3.2)式得
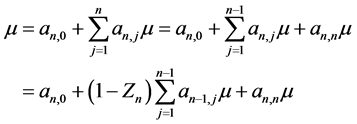 (3.6)
(3.6)
由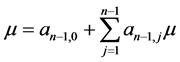 得
得
 (3.7)
(3.7)
由(3.6)式和(3.7)式得
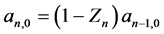 (3.8)
(3.8)
由(3.5)式和(3.8)式得
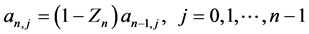 (3.9)
(3.9)
因此
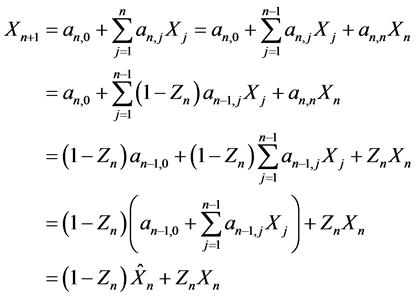 。
。
引理2
假设保单合同前n年的历史索赔数据是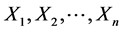 ,则在假设1和假设2条件下的最大熵损失估计有如下关系成立:
,则在假设1和假设2条件下的最大熵损失估计有如下关系成立:
i) n + 1年的预测保费为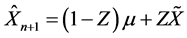
其中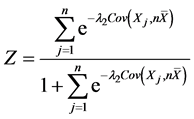 ,
,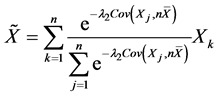
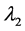 是方程
是方程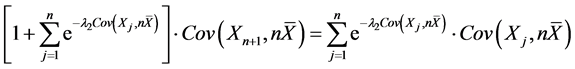 的解。
的解。
ii)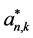 满足
满足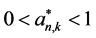 。
。
iii) 当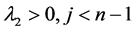 时
时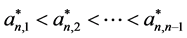 。
。
iv) 当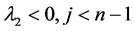 时
时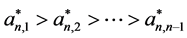 。
。
引理2的证明
(i) 取线性预测形式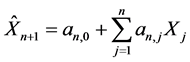 并假设
并假设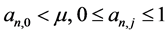
首先求解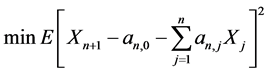
得 和
和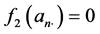 其中
其中
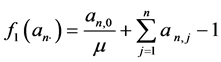 (3.10)
(3.10)
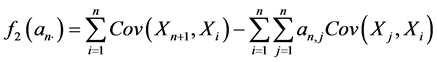 (3.11)
(3.11)
由拉格朗日乘子法得
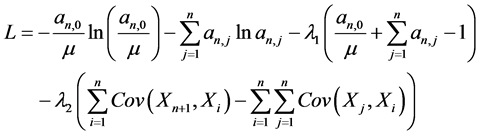 (3.12)
(3.12)
对(3.12)关于 求导并令导数为0得
求导并令导数为0得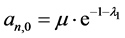 。
。
将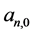 代入(3.12)得
代入(3.12)得
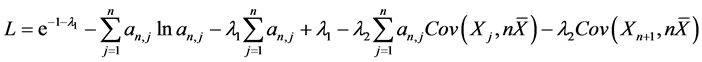 (3.13)
(3.13)
对(3.13)关于 求导并令导数为0得
求导并令导数为0得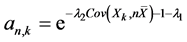 。
。
将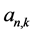 代入(3.13)得
代入(3.13)得
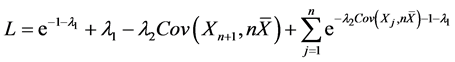 (3.14)
(3.14)
对(3.14)关于 求导并令导数为0得
求导并令导数为0得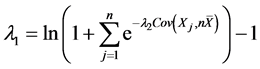
将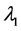 代入以上式子得
代入以上式子得

其中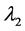 是方程
是方程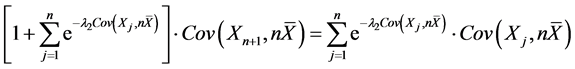 的解,
的解,
此方程由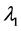 代入(3.14)关于
代入(3.14)关于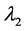 求导得到。
求导得到。
因此,n + 1年的预测保费

其中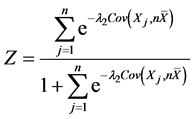 ,
,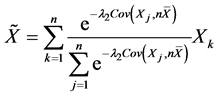 。
。
(ii) 因为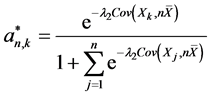 ,且
,且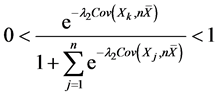
所以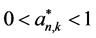 。
。
(iii) 当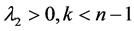 时
时
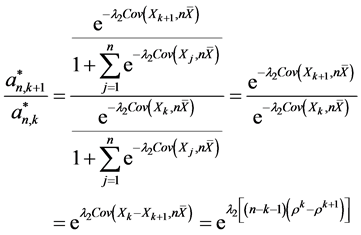
因为 所以
所以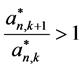
所以 。
。
(iv) 当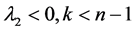 时
时

因为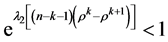 。
。
Table 1. Simulation results
表1. 模拟结果
所以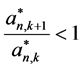
所以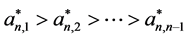 。
。
定理1
假设保单合同前n的历史索赔数据是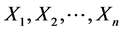 ,则在最大熵方法下,n + 1年保费的递推估计为
,则在最大熵方法下,n + 1年保费的递推估计为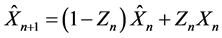 。
。
其中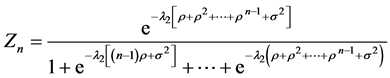 。
。
定理1的证明
在假设1和2下,由引理1和2得,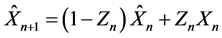
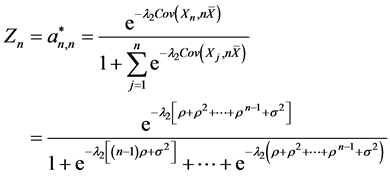 。
。
4. 数值模拟
在本节对前面的结果进行数值模拟,为说明问题,假设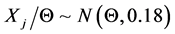 ,
, ,取
,取 ,
,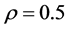 ,重复执行10000次模拟,得到信度估计均值与标准差如表1。
,重复执行10000次模拟,得到信度估计均值与标准差如表1。
在表1的模拟结果中,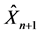 为10000次模拟产生的第n + 1年保费的均值,而std为相应信度保费与参数真值产生的标准差,从结果可以看出,模拟出来的信度保费与真实保费较为接近。
为10000次模拟产生的第n + 1年保费的均值,而std为相应信度保费与参数真值产生的标准差,从结果可以看出,模拟出来的信度保费与真实保费较为接近。
5. 结论
本文将最大熵方法与递推信度模型结合在一起,首先得到下一年保费的递推预测形式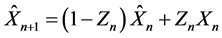 ,并给出信度因子
,并给出信度因子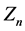 的表达式,从中可以看出信度因子是变化的;然后,得到了两种特殊的权重结构:一种是年份较近的索赔额有较大权重,另一种是年份较远的索赔额有较大的权重。
的表达式,从中可以看出信度因子是变化的;然后,得到了两种特殊的权重结构:一种是年份较近的索赔额有较大权重,另一种是年份较远的索赔额有较大的权重。
文章引用
张兴红,吴黎军. 最大熵方法下的递推信度模型
The Recursive Credibility Model of Maximum Entropy Method[J]. 统计学与应用, 2017, 06(02): 111-118. http://dx.doi.org/10.12677/SA.2017.62013
参考文献 (References)
- 1. Buhlmann, H. (1967) Experience Rating and Credibility. ASTIN Bulletin, 4, 199-207. https://doi.org/10.1017/S0515036100008989
- 2. Gerber, H.U. and Jones, D.A. (1975) Credibility Formulas of the Updating Type. In: Credibility Theory and Application, Academic Press, Cambridge, 89-109.
- 3. Atanasiu, V. (2009) Some Extensions of the Buhlmann-Straub Credibility Formulae. Buletinul Academiei de Stiinte a Republicii Moldova, 3, 3-12.
- 4. Atanasiu, V. (2013) Application of the Credibility Theory Based on Important Mathematical Properties. Applied Sciences, 15, 13-29.
- 5. 胡莹莹, 吴黎军, 孙毅. 指数保费原理下的递归信度模型[J]. 黑龙江大学自然科学学报, 2015, 32(3): 319-324.
- 6. Jaynes, E.T. (1957) In-formation Theory and Statistical Mechanics. Physical Reviews, 106, 620-630. https://doi.org/10.1103/PhysRev.106.620
- 7. Jessop, A. (1999) Entropy in Multi-Attribute Problems. Journal of Multi-Criteria Decision Analysis, 8, 61-70. https://doi.org/10.1002/(SICI)1099-1360(199903)8:2<61::AID-MCDA230>3.0.CO;2-P
- 8. Landsmann, Z. (1999) Credibility Evaluation for the Exponential Dispersion Family. Insurance: Mathematics and Economics, 24, 23-29.
- 9. Payandeh Najafabadi, A.T. (2012) A Maximum-Entropy Approach to the Linear Credibility Formula. Insurance: Mathematics and Economics, 51, 216-221.
- 10. 胡莹莹, 吴黎军, 孙毅. 最大熵方法下的纯稳健信度估计[J]. 河南师范大学自然科学学报, 2016, 44(1): 15-20.
