Statistics and Application
Vol.07 No.01(2018), Article ID:23225,6
pages
10.12677/SA.2018.71001
Simulation of Stochastic Stability of Delayed IS-LM Model with Markovian Switching
Lujun Zhou
College of Economics, Hunan Agricultural University, Changsha Hunan
Received: Dec. 7th, 2017; accepted: Dec. 21st, 2017; published: Dec. 28th, 2017

ABSTRACT
This paper studies that the economic system is in the random environment which has delayed time in taxation and Markov chain with two discrete values. By using the method of stochastic stability and the given parameters, this paper analyzes the stability and simulation of the solution of the standard random IS-LM model with Markovian Switching and delayed time.
Keywords:IS-LM Model, Stochastic Delayed Differential Equation, Markov Chain, Stability
马尔可夫调制的随机时滞IS-LM模型的 随机稳定性仿真
周路军
湖南农业大学经济学院,湖南 长沙
收稿日期:2017年12月7日;录用日期:2017年12月21日;发布日期:2017年12月28日

摘 要
本文研究了标准随机IS-LM模型处于税收过程中存在时滞及二元离散状态值的马尔可夫链随机性波动环境中,在给定参数条件下通过利用随机稳定性方法探讨了马尔可夫调制的标准随机时滞IS-LM模型的指数稳定性行为,得到了解的仿真结果。
关键词 :IS-LM模型,随机时滞微分方程,马尔可夫链,稳定性

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随机微分方程一般常用来描述经济系统的不确定性因素的影响,而如自然灾害的突然发生,或者经济政策的改变,或者企业生产技术的革新等会带来经济系统结构性的变化,因此具有离散状态特征的马氏链也会引入到随机微分方程中。
所以,具有马尔可夫链调制的随机微分方程与随机时滞微分方程的研究大量应用于经济、金融、控制等领域,其相应的稳定性理论、控制理论与数值仿真得到了极大的发展。
在标准的IS-LM经济周期模型应用方面,马氏链调制的随机IS-LM经济周期模型的研究尚少,尤其是模型中考虑到税收过程中存在时滞的情形,研究更少。本文考虑两状态的马尔可夫链到随机时滞IS-LM模型中,研究它的随机稳定性并给出数值仿真例子。
2. 预备知识及模型构建
Mao (2001)研究了如下的马尔可夫调制的随机微分方程 [1] :
这里 ,具有初始值 。
假如A是一个向量,则用 表示Rn中欧氏范数。假如A是一个矩阵(用AT表示A的转置),则定义 为迹范数,定义 为算子范数。设 是定义在完备概率空间 上的右连续马尔可夫链,取两个值的状态空间 ,且具有生成元 ,其中
这里 , 是由i状态转移到j状态的转移速率,且 。
马尔可夫链 与布朗运动 假设是相互独立的,则 的每一个样本轨迹都是一个右连续的阶梯函数,且在每一个有限子区间上只有有限个跳跃点。
V. Torre (1977)用分岔理论分析了非均衡市场的完全凯恩斯系统 [2]
其中 ;Y,R,I(Y,R),S(Y,R),L(Y,R),Ls, 和 分别表示产品供给函数、利率、投资(产出和利率的函数)、储蓄(产出和利率的函数)、货币流动需求量、常数货币流动供给量、产品市场和货币市场调整参数。第一个方程表示产品市场的非均衡调整,第二个表示货币市场的非均衡调整。
本文中的第一个方程利用萨谬尔森的动态乘数-加速数模型 [3] 的第一个方程即 ,其中需求函数 表示成消费函数、投资函数及政府支出的和。而消费函数 是关于可支配收入的函数。税收函数是产品供给函数的正常数倍,且税收过程中存在时间延迟现象,因此引入时滞 ,税收函数为 ;投资函数是关于供给和利率的函数 ;G是常数政府支出。
本文第二个方程中假设流动性需求函数 ,供给函数 是常数。则考虑的时滞IS-LM模型为
(1)
这里参数 。
命题1:在条件 和 都满足的情况下,标准时滞IS-LM模型(1)存在唯一的正均衡解
。
令 , ,则模型(1)变成
(2)
由于此系统受到随机扰动的影响,令变量 , 和 对应的参数在两个方程中分别受到强度为 , , , 和 的随机扰动。
即模型(2)变为
(3)
用矩阵表示为
(4)
这里
, 。
考虑到上涨与紧缩周期性波动的影响,将二值离散状态的马尔可夫链 引入到模型(4),则模型变成
(5)
这里r(t) = 1,2。生成元
3. 案例仿真
例令
,
,
,
及生成元 。
命题1条件 满足,则模型(5)存在唯一平凡均衡解。
通过Euler-Maruyama方法 [4] 对案例进行MATLAB仿真,分别在两个不同随机样本和不同时滞( )下,得到图1,图2,图3,图4。
图1,图2描述的是在时滞为0.2的情况下两种不同随机样本下,模型(5)的解在时间t < 50以内波动性非常大。但随着时间t的增加(t > 150)模型(5)的解在不断地趋近于平凡均衡解。总体上呈现随机稳定。
图3,图4描述的是模型(5)在时滞为0.8的两种不同随机样本情况。图3中,模型(5)的解在时间t < 50以内波动性非常大,但随着时间t的增加(t > 150)在不断地趋近于均衡解。而图4中,模型(5)的解在时间t < 150以内波动性都非常大,而在t > 150后波动性较少且不断地趋近于均衡解。总体上都呈现随机稳定。

Figure 1. Solution x(t), y(t) of sde and r(t) (time lag = 0.2)
图1. 随机微分方程解x(t),y(t)及马氏链r(t) (时滞 = 0.2)

Figure 2. Solution x(t), y(t) of sde and r(t) (time lag = 0.2)
图2. 随机微分方程解x(t),y(t)及马氏链r(t) (时滞 = 0.2)
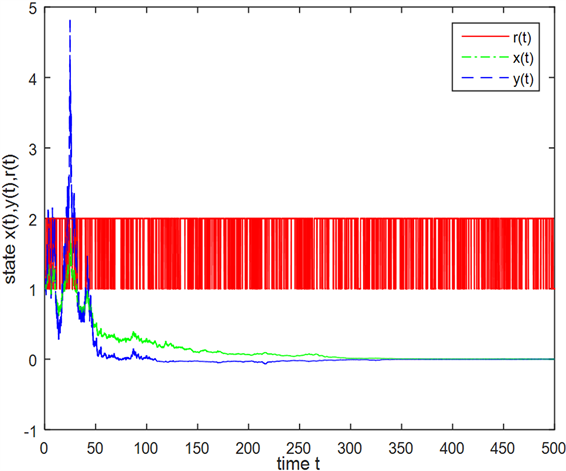
Figure 3. Solution x(t), y(t) of sde and r(t) (time lag = 0.8)
图3. 随机微分方程解x(t),y(t)及马氏链r(t) (时滞 = 0.8)
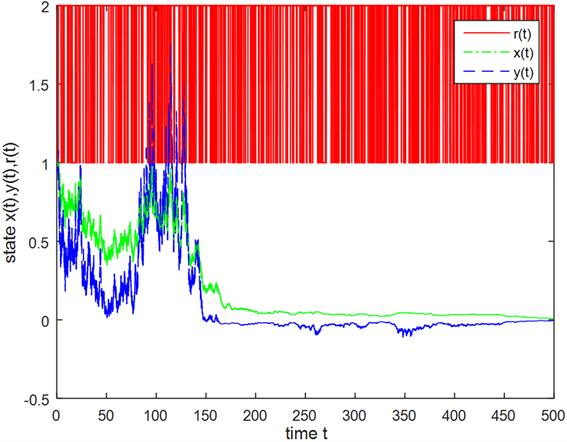
Figure 4. Solution x(t), y(t) of sde and r(t) (time lag = 0.8)
图4. 随机微分方程解x(t),y(t)及马氏链r(t) (时滞 = 0.8)
从图1~图4看出,r(t)是一个连续的阶梯函数,且在固定的子区间里是有限跳跃的。
基金项目
教育部人文社会科学研究一般项目(11YJCZH259)。
文章引用
周路军. 马尔可夫调制的随机时滞IS-LM模型的随机稳定性仿真
Simulation of Stochastic Stability of Delayed IS-LM Model with Markovian Switching[J]. 统计学与应用, 2018, 07(01): 1-6. http://dx.doi.org/10.12677/SA.2018.71001
参考文献 (References)
- 1. Mao, X., Matasov, A. and Piunovskiy, A.B. (2000) Stochastic Differential Delay Equations with Markovian Switching. Bernoulli, 1, 73-90. https://doi.org/10.2307/3318634
- 2. Torre, V. (1977) The Existence of Limit Cycles and Control in Complete Keynesian Systems by Theory of Bifurcations. Econometrica, 45, 1457-1466. https://doi.org/10.2307/1912311
- 3. Turnovsky, S.J. (1996) Methods of Macroeconomic Dynamics. MIT Press, Boston.
- 4. Bing, L., Dingshi, L. and Daoyi, X. (2013) Stability Analysis for Impulsive Stochastic Delay Differential Equations with Markovian Switching. Journal of the Franklin Institute, 350, 1848-1864.