Statistics and Application
Vol.07 No.02(2018), Article ID:24322,11
pages
10.12677/SA.2018.72011
Moving Ratio Test for Multiple Mean Changes in Long Memory Time Series with Applications
Guolong Fu*, Mingcan He
Department of Mathematics and Statistics, Qinghai Normal University, Xining Qinghai

Received: Mar. 12th, 2018; accepted: Mar. 28th, 2018; published: Apr. 4th, 2018

ABSTRACT
In this paper, by introducing a bandwidth parameter, a moving ratio type statistic is proposed to detect multiple mean changes in long memory time series. The null distribution of the test statistic and its consistency under the alternative hypothesis are proved. Simulations show that the proposed new method can effectively solve the problem of testing failure when using the single change point test method to test multiple change points. Finally, the practicability of the method is illustrated by two groups of actual data.
Keywords:Long Memory Time Series, Mean Change Point, Moving Ratio Statistics
长记忆时间序列均值多变点滑动比检验及应用
付国龙*,何明灿
青海师范大学数学与统计学院,青海 西宁

收稿日期:2018年3月12日;录用日期:2018年3月28日;发布日期:2018年4月4日

摘 要
本文通过引进一个窗宽参数,提出了一种滑动比率型统计量来检验长记忆时间序中的列均值多变点。在原假设下给出了检验统计量的极限分布,在备择假设下证明了检验方法的一致性。模拟结果表明,提出的新方法能够有效解决单变点检验方法在数据中存在多个变点时检验失效的问题,最后通过两组实际数据说明了该方法的实用性。
关键词 :长记忆时间序列,均值多变点,滑动比统计量

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在过去几十年里,检验各类模型和数据中的变点问题一直是统计学,计量经济学和一些应用学科中的热点问题。均值变点作为一类最常见的变点,文献中已有大量研究,常见的均值变点检验方法主要有CUSUM方法、似然比方法、最小二乘法、Wald检验等。但现有的大部分文献主要研究的是独立序列或短期相依序列中的均值变点问题。越来越多的证据表明,许多气象、经济、金融等时间序列具有长记忆性,无法用传统的短记忆时间序列模型刻画,这使得检验长记忆时间序列模型中的均值变点问题也变的非常重要。
Hidalgo和Robinson [1] 在假定变点位置已知的情况下,提出了一种检验长记忆时间序列均值变点的Wald方法,Wright [2] 在变点位置未知的情况下,研究了长记忆时间序列中的均值变点,并提出了一种CUSUM检验方法和一种Sup-Wald检验方法。Lazarova [3] 研究了线性回归模型含有长记忆时间序列误差项时结构变点的检验问题,Wang [4] 研究了无限滑动平均时间序列均值变点的检验和估计问题,Shao [5] 通过提出一种简单的比率型统计量继续研究长记忆时间序列均值变点的检验问题,这种比率型检验方法的有点是不需要估计尺度参数等冗余参数,在实际应用中非常方便。赵文芝等 [6] ,马健琦等 [7] 提出了一些新的比率型统计量来检验长记忆时间序列中的均值变点,模拟结果表明这些新比率统计量具有比原比率型统计量更高的检验势。
上述关于长记忆时间序列均值变点检验的文献均考虑的是单变点问题,由于数据中存在变点时,不一定只有一个变点,而基于单变点问题设计的检验方法在多变点检验问题中通常不适用,所以研究长记忆时间序列均值多变点的检验问题也很重要。如今也有许多检验多变点问题的文献,如Kejriwal [8] 利用Wald检验方法研究了时间序列中持久性均值多变点问题,Bai [9] 用似然比检验方法检验了短记忆时间序列中的均值多变点问题,秦瑞兵等 [10] 提出了检验独立随机序列均值多变点的非参数方法,Chen [11] [12] 等利用滑动比率方法研究了时间序列中持久性多变点的检验和估计问题。
比率型检验方法由于不需要估计尺度参数,所以在应用中非常方便,但现有的基于比率型方法检验长记忆时间序列均值变点的研究都只考虑的是单变点问题,本文试图将比率型方法推广到均值多变点的检验问题当中去。推广的基本思想是通过引进一个窗宽参数,利用滑动的方法比较当前时刻前后一段时间内的样本差异,并决策是否存在变点。由于通过窗宽可以进入统计量中的样本中至多只有一个变点,所以可以避免多变点改变统计量不单调的问题,从而达到检测多变点问题的最终目的。第4节的模拟结果表明,本文采用的改进方法行之有效。
2. 长记忆模型和检验统计量
令
,
这里B是置后算子,m是 的无条件均值, 是均值为0,具有有限方差的独立同分布的平稳序列,n为样本容量,当参数 时,称时间序列 是长记忆时间序列,记为 。参数d称为长记忆参数,当 时, 为平稳序列,而当 时, 为非平稳长记忆序列。长记忆时间序列 可分解为如下形式:
, , , .
其中 是gamma函数。
设 其中 , ,本文考虑平稳长记忆时间序列均值多变点的检验问题,即考虑如下假设检验问题:
即在备择假设下长记忆时间序列 的均值:
其中 不全相等,若定义
.
则上述假设检验问题可转换为:
: ;
: 至少有一个不为零。
这里m是变点的个数,当 时,Shao [5] 提出了如下比率统计量
, (1)
其中
, , , .
上述检验统计量的优点是不需要估计样本方差,所以在实际应用中非常方便,但该统计量只能检验单个均值变点,为了使该方法在多变点问题中仍然有效,本文提出如下修正统计量:
(2)
其中 ,若定义窗宽 ,则 , , 表示取整。为推导该统计量的极限分布,需做如下假设:
假设1:在备择假设下,两个均值变点之间最少有 个样本。
假设2:当 时,存在一个 ,使得
,
其中, 为一个常数, 表示分数布朗运动。
假设1保证变点可以被区分,这在多变点检验问题中是基本假设。假设2同Shao [5] 中的假设1,是长记忆时间序列所满足的中心极限定理。
3. 检验统计量的渐近性质
本节将给出检验统计量(2)在原假设下的极限分布,并证明检验方法在备择假设下的一致性。
定理1:在原假设 成立的条件下,当 时,有
其中
证明:令 , 则由假设2有:
同理可得
因此
证毕。
定理2:若假设1成立,则当数据中至少存在一个均值变点 时,有
.
证明:由假设1,任意两个变点间至少有2L个样本,而统计量 只用到了当前时刻前后共2L个样本,即这些样本中至多只有一个变点,因此只需要证明变点个数 的情况即可。不妨记变点时刻为 ,则,当 时,
由于 和 分别只用到了变点 之前的L个样本和变点之后的L个样本,所以由定理1的证明有
从而统计量 的分母为 ,若记 在变点 时刻由常数m变为 , ,另一方面,统计量 的分子
其中
即 。而 。因此,当 ,即 时,有 。证毕。
4. 数值模拟
本节基于 模型通过模拟实验研究本文提出的统计量(2)的有限样本性质,并和Shao的统计量(1)作比较。在统计量(1)中参数t分别取0.1和0.2,修正后的统计量(2)中的窗宽参数h同样取0.1和0.2,所有的结果都是利用R语言模拟10000次得到的。本文所用到的临界值是由数据生成过程 生成10000组容量为10000的随机序列计算所得。在模拟实验中,分别取样本容量为100和400,长记忆参数取0、0.2和0.4。
表1给出了原假设下两种检验统计量在5%检验水平下的经验水平,可以看出两种方法在所有参数组合下都能较好的控制经验水平。比较而言,本文提出的修正统计量在样本量较小时相对保守一些,长记忆参数d对经验水平的影响不明显。
为检验两种统计量的检验势,分别考虑数据中存在m = 1、2和3个变点的情况,跳跃度D分别取1和2,变点位置k*分别取0.25、0.5和0.8。表2和表3分别列出了两种检验统计量在变点个数m = 1时的
Table 1. Empirical size of the two statistics at the 5% test level
表1. 两种统计量在5%检验水平下的经验水平
Table 2. Number of modified Shao statistics at change points m = 1 and empirical power at the 5% level
表2. 修正的Shao统计量在变点个数m = 1,经验水平为5%时的经验势
Table 3. Number of Shao statistics at change points m=1 and empirical power at the 5% level
表3. Shao统计量在变点个数m = 1,经验水平为5%时的经验势
检验势。从中可以看出,随着样本容量的增大和跳跃度的增大,两个统计量的检验势都逐渐增大,这验证了两个统计量都是一致检验的定理结论。此外,随着长记忆参数d的增大,检验势逐渐降低,变点位置越靠近中间时检验势也越高。由于本文检验统计量只用了部分样本,所以在数据中只有1个变点时,本文的修正检验统计量的检验势低于原统计量,但随着样本容量的增大和窗宽参数的增大,这种差距逐渐减小。
表4~7分别给出了两个统计量在变点个数m取值为2和3时的检验势,此时可以发现本文提出的滑动比率方法的经验势普遍高于原统计量,尤其在m取3时更为显著。在大部分情况下,原统计量均很难检测到变点,这说明本文基于部分样本的滑动比率方法在多变点的检验问题中是可行的。由于在实际问题中无法提前知道数据中有几个变点,所以可以两种方法同时使用,如果两种方法都不拒绝无变点的原假设,则可认为数据中不存在变点;若至少有一个统计量拒绝原假设则可认为数据中存在变点。特别地,若统计量(1)没有拒绝原假设,而统计量(2)拒绝了原假设。则可怀疑数据中存在多个变点,需进一步仔细分析。
5. 实例分析
本节用两组实际数据来验证本文所述的假设检验问题。第一组数据选自从1871年到1970年尼罗河阿斯旺水坝年度流量数据(见图1),第二组数据选自从1854年到1989年北半球气温数据(见图2),Shao [5] 基于统计量(1)检验发现这两组数据中存在一个均值变点。下面利用本文提出的新统计量重新检验这两组数据,第一组数据中发现当 时,检验统计量(2)在第28个样本处达到最大值52.614,其对应的临界值为34.73,当 时,检验统计量(2)在第28个样本处达到最大值37.65,其对应的临界值为22.784,由于统计量的值大于对应的临界值,说明该数据集在第28个样本处发生了变化。经计算发现前28个样本的均值为1097.75,后72个样本的均值为849.972,前后差异较大,说明该组数据在第28个样本处存在变点,该结果与Shao的检验结果相一致。同样的,对于第二组数据发现当 和 时,检验统计量(2)在第826个样本处达到最大值75.28,用同样的检验方法发现该组数据在第826个样本处存在均值变点,该结果也与Shao的检验结果相一致。
Table 4. Number of Shao statistics at change points m = 2 and empirical power at the 5% level
表4. 修正的Shao统计量在变点个数m = 2,经验水平为5%时的经验势
6. 总结
本文研究了长记忆时间序列均值多变点的检验问题,基于已有的一种比率型统计量,通过引进一个窗宽参数,提出了一种滑动比率型检验统计量。在原假设下推导出了新统计量的极限分布,在备择假设下证明了统计量的一致性,并通过蒙特卡罗模拟说明了本文所选方法的有效性,最后通过一组实际数据说明了本文方法的可行性。由于本问提出的滑动比率方法相对更保守,且在数据中只有一个变点时,检验势低于原检验方法,所以建议在实际问题中两种方法同时使用,如果两种方法都不拒绝无变点的原假设,则可认为数据中不存在变点;若至少有一个统计量拒绝原假设则可认为数据中存在变点。特别地,若原没有拒绝原假设,而本文提出的新统计量拒绝了原假设,则可怀疑数据中存在多个变点,需进一步仔细分析。
Table 5. Number of Shao statistics at change points m = 2 and empirical power at the 5% level
表5. Shao统计量在变点个数m = 2,经验水平为5%时的经验势
Table 6. The empirical power of the modified Shao statistic when the number of change points is m = 3, the position of change point is 0.25, 0.5, 0.8, and the empirical level is 5%
表6. 修正的Shao统计量在变点个数m = 3,变点位置分别为0.25、0.5、0.8,经验水平为5%时的经验势
Table 7. The empirical power of the Shao statistic when the number of change points is m = 3, the position of change point is 0.25, 0.5, 0.8, and the empirical level is 5%
表7. Shao统计量在变点个数m = 3,变点位置分别为0.25、0.5、0.8经验水平为5%时的经验势
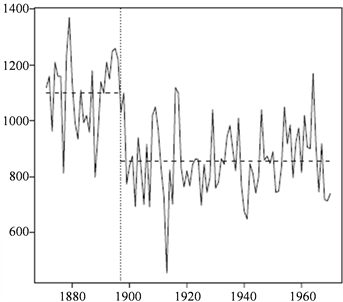
Figure 1. Annual flow time series of the Nile Aswan Dam
图1. 尼罗河阿斯旺水坝年度流量时间序列图

Figure 2. Time series of annual temperature data in the northern hemisphere
图2. 北半球年度气温数据时间序列图
致谢
在此,我要感谢我的导师陈占寿老师,感谢陈老师对我在生活上的关心和学业上的精心指导。他严谨求实、精益求精的治学态度和对专业前沿问题敏锐的洞察力深深地影响了我,使我不仅学到了本专业的理论知识,而且培养了我发现问题、分析问题、解决问题的能力,使我终身受益。我还要感谢国家自然科学青年基金、青海省自然科学青年基金的资助,以及所引用文献的作者对科学做出的贡献。
基金项目
国家自然科学青年基金(11301291, 11661067),青海省自然科学基金(2015-ZJ-717)资助。
文章引用
付国龙,何明灿. 长记忆时间序列均值多变点滑动比检验及应用
Moving Ratio Test for Multiple Mean Changes in Long Memory Time Series with Applications[J]. 统计学与应用, 2018, 07(02): 79-89. https://doi.org/10.12677/SA.2018.72011
参考文献
- 1. Hidalgo, J. and Robinson, P.M. (1996) Testing for Structural Change in a Long-Memory Environment. Journal of Economerics, 70, 159-174. https://doi.org/10.1016/0304-4076(94)01687-9
- 2. Wright, J.H. (2010) Testing for a Structural Break at Un-known Date with Long-Memory Disturbances. Journal of Time Series Analysis, 19, 369-376. https://doi.org/10.1111/1467-9892.00097
- 3. Štěpána, L. (2005) Testing for Structural Change in Regression with Long Memory Processes. Journal of Econometrics, 129, 329-372. https://doi.org/10.1016/j.jeconom.2004.09.011
- 4. Wang, L. (2008) Change-in-Mean Problem for Long Memory Time Series Models with Applications. Journal of Statistical Computation & Simulation, 78, 653-668. https://doi.org/10.1080/00949650701216604
- 5. Shao, X. (2011) A Simple Test of Changes in Mean in the Possible Presence of Long-Range Dependence. Journal of Time Series Analysis, 32, 598-606. https://doi.org/10.1111/j.1467-9892.2010.00717.x
- 6. 赵文芝, 夏志明, 贺飞跃. 长相依序列均值变点检测[J]. 数学的实践与认识, 2016, 46(3): 204-208.
- 7. 马健琦, 陈占寿, 吕娜. 基于Sieve Bootstrap方法的长记忆过程均值变点的检验[J]. 青海师范大学学报(自科版), 2017, 33(2): 34-38.
- 8. Kejriwal, M. and Zhou, J. (2013) Wald Tests for Detecting Multiple Struc-tural Changes in Persistence. Econometric Theory, 29, 289-323. https://doi.org/10.1017/S0266466612000357
- 9. Bai, J. (1999) Likelihood Ratio Tests for Multiple Structural Changes. Journal of Econometrics, 91, 299-323. https://doi.org/10.1016/S0304-4076(98)00079-7
- 10. 秦瑞兵, 田铮, 陈占寿. 独立随机序列均值多变点的非参数检测[J]. 应用概率统计, 2013, 29(5): 449-457.
- 11. Chen, Z., Tian, Z., et al. (2012) Moving Ratio Test for Multiple Changes in Persis-tence. Journal of Systems Science & Complexity, 25, 582-593. https://doi.org/10.1007/s11424-012-9255-9
- 12. Chen, Z., Jin, Z., Tian, Z., et al. (2012) Bootstrap Testing Multiple Changes in Persistence for a Heavy-Tailed Sequence. Computational Statistics & Data Analysis, 56, 2303-2316. https://doi.org/10.1016/j.csda.2012.01.011
NOTES
*通讯作者。
