Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21057,3
pages
10.12677/AAM.2017.64049
Using Monotonicity and Limit to Judge the Positive and Negative of a Function
Xuhui Tong, Qianqian Ye
School of Mathematics and Information, Zhejiang Ocean University, Zhoushan Zhejiang

Received: Jun. 1st, 2017; accepted: Jun. 19th, 2017; published: Jun. 21st, 2017

ABSTRACT
In this paper, the positive and negative problems (a, b can be infinite) of the derivative function f(x) on the interval (a, b) are studied. By using the monotonicity of the function and the relationship between the limit value and the zero at the end point, three sufficient conditions for the positive and negative properties of the judgment function f(x) on the interval (a, b) are deduced, and finally through the three examples to show that the conclusion of this paper can be used to prove some specific problems more easily.
Keywords:Monotonicity, Limit, Positive and Negative
利用单调性与极限判断函数的正负性
童旭辉,叶倩倩
浙江海洋大学数理与信息学院,浙江 舟山
收稿日期:2017年6月1日;录用日期:2017年6月19日;发布日期:2017年6月21日

摘 要
本文主要研究在区间 上的可导函数
上的可导函数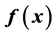 的正负性问题(
的正负性问题( 可以为无穷)。借助于函数的单调性和在端点处的极限值与零的大小关系,推导出了判断函数
可以为无穷)。借助于函数的单调性和在端点处的极限值与零的大小关系,推导出了判断函数 在区间
在区间 上的正负性的三个充分条件,最后通过三个例题表明用本文的结论可以更加简便地证明一些具体问题。
上的正负性的三个充分条件,最后通过三个例题表明用本文的结论可以更加简便地证明一些具体问题。
关键词 :单调性,极限,正负性

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在函数的研究过程中,我们少不了对函数在其定义域内的正负性的研究。比如在研究含参变量的二次函数问题时,我们必然会探究二次函数的根的判别式 的正负性问题。若
的正负性问题。若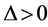 ,则二次函数在其定义域有两根;若
,则二次函数在其定义域有两根;若 ,则二次函数在其定义域有无根。又如,在探究函数的图像问题时,我们必定会研究函数的单调性与凹凸性问题。若函数
,则二次函数在其定义域有无根。又如,在探究函数的图像问题时,我们必定会研究函数的单调性与凹凸性问题。若函数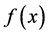 在某区间内的一阶导数
在某区间内的一阶导数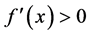 ,则函数
,则函数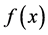 在此区间上为增函数;反之,则为减函数。若函数
在此区间上为增函数;反之,则为减函数。若函数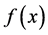 在此区间内的二阶导数
在此区间内的二阶导数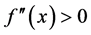 ,则函数在此区间上为凹函数;反之,则为凸函数 [1] [2] 。
,则函数在此区间上为凹函数;反之,则为凸函数 [1] [2] 。
在判断函数 在闭区间
在闭区间 上的正负性时,我们通常的做法是:先求出函数
上的正负性时,我们通常的做法是:先求出函数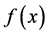 在
在 内的驻点和导数不存在的点,若函数
内的驻点和导数不存在的点,若函数 在驻点、导数不存在的点和区间端点处的函数值均大于0,则函数在区间
在驻点、导数不存在的点和区间端点处的函数值均大于0,则函数在区间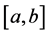 上恒正;反之,恒负。这一判断过程较为繁琐,且若函数
上恒正;反之,恒负。这一判断过程较为繁琐,且若函数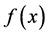 在端点处的函数值不存在或者区间
在端点处的函数值不存在或者区间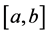 为无穷区间时,那么这个判断方法就不适用了。本文另辟蹊径,借助于函数的单调性的性质和在端点处的极限方法,推导出了判断函数
为无穷区间时,那么这个判断方法就不适用了。本文另辟蹊径,借助于函数的单调性的性质和在端点处的极限方法,推导出了判断函数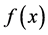 在区间
在区间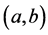 上的正负性的三个充分条件,以此就可以无需计算函数在端点处的函数值,就可以简单快速地判断出函数在某可导区间上的正负性,使得求解过程更加简洁、直观。
上的正负性的三个充分条件,以此就可以无需计算函数在端点处的函数值,就可以简单快速地判断出函数在某可导区间上的正负性,使得求解过程更加简洁、直观。
2. 主要结果
区间 上的可导函数
上的可导函数 的正负性判断定理如下(
的正负性判断定理如下(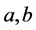 可以为无穷)。
可以为无穷)。
定理2.1. 若 ,且
,且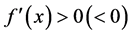 ,则
,则 ,
, 。
。
证:下证 ,
,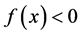 的情形可类似证明。
的情形可类似证明。
因为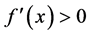 ,所以
,所以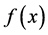 在
在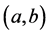 内严格单调增加。
内严格单调增加。
又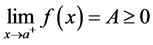 ,故
,故 ,
, 。
。
定理2.2. 若 ,且
,且 ,则
,则 ,
, 。
。
证明方法与定理2.1类似 [3] 。
定理2.3. 若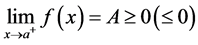 ,且
,且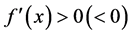 ,
, ;若
;若 ,且
,且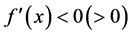 ,
, ,则当
,则当 时,
时,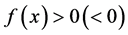 。
。
证:下证 ,
,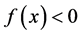 的情形可类似证明。
的情形可类似证明。
由定理2.1与定理2.2可知:
 ,
,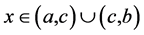
只需证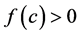 即可。
即可。
易知 是
是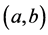 上的连续函数,由连续性知:
上的连续函数,由连续性知:
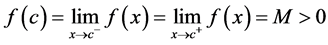
综上,可知当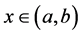 时,
时, 。
。
注1:定理2.3中,由其证明过程可以看出 在点
在点 处可以弱化为连续,甚至可以是单侧连续,不必可导也可。
处可以弱化为连续,甚至可以是单侧连续,不必可导也可。
3. 应用
例3.1.判断 在
在 上的正负性。
上的正负性。
解:因为

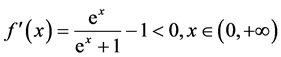
由定理2.2可知 在
在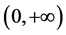 上恒正。
上恒正。
例3.2.判断 在
在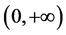 上的正负性。
上的正负性。
解: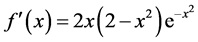
易知
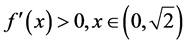 ;
;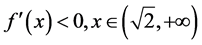
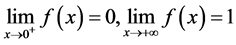
由定理2.3可知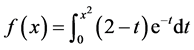 在
在 上恒正。
上恒正。
例3.3.判断分段函数 的正负性。
的正负性。
解: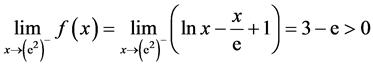 ,
,
当 时,
时,
又
当 时,
时,
易知 在点
在点 处是右连续的,
处是右连续的,
由注1可知 恒正。
恒正。
文章引用
童旭辉,叶倩倩. 利用单调性与极限判断函数的正负性
Using Monotonicity and Limit to Judge thePositive and Negative of a Function[J]. 应用数学进展, 2017, 06(04): 423-425. http://dx.doi.org/10.12677/AAM.2017.64049
参考文献 (References)
- 1. 华东师范大学数学系. 数学分析(上册) [M]. 第4版. 北京: 高等教育出版社, 2010.
- 2. 华东师范大学数学系. 数学分析(下册) [M]. 第4版. 北京: 高等教育出版社, 2010.
- 3. 钱吉林. 数学分析解题精粹[M]. 第2版. 武汉: 湖北长江出版集团, 2011.