Advances in Applied Mathematics
Vol.06 No.08(2017), Article ID:22688,9
pages
10.12677/AAM.2017.68110
Dynamical Behaviors of the H7N9 Avian Influenza with Latent Period
Yafei Zhao, Qiang Su, Guichen Lv*
Chongqing University of Technology, Chongqing
*通讯作者。

Received: Oct. 27th, 2017; accepted: Nov. 9th, 2017; published: Nov. 16th, 2017

ABSTRACT
In this paper, we investigate the dynamics of the H7N9 avian influenza with latent period. By applying LaSalle invariance principle, Bendixson-Dulac criterion and Li-Muldowney’s geometric approach, some results for the global asymptotic stability of the human-poultry system are obtained.
Keywords:SI-SEIR Model, Basic Reproductive Number, Global Asymptotic Stability
具有潜伏效应的H7N9型禽流感模型的动力学分析
赵亚飞,苏强,吕贵臣*
重庆理工大学,重庆

收稿日期:2017年10月27日;录用日期:2017年11月9日;发布日期:2017年11月16日

摘 要
本文研究了具有潜伏期的H7N9禽流感病毒的动力学行为。利用LaSalle不变性原理、Bendixson-Dulac判据以及Li-Muldowney几何方法给出了人–禽系统的全局稳定性。
关键词 :SI-SEIR模型,基本再生数,全局稳定性

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
禽流感病毒与人流感病毒存在受体特异性差异,通常只在禽类中传播,一般情况下不会传染给人类。H7N9型病毒是一种甲型禽流感病毒,在禽中有高致病力。2003年3月首次发现人类感染H7N9禽流感病例,2013年3月,我国出现了一种新型H7N9亚型禽流感病毒,在禽中有低致病力而对人类有高致病力,这引起了人们的高度重视。从2013年初,通过《国际卫生条例》报告途径迄今已报告了总共1486例人感染甲型H7N9禽流感病毒实验室确诊病例 [1] 。携病毒禽类是禽流感在人类中传播的源头,找到防控禽类染病的方法致使有效减少人类感染禽流感病毒的问题亟待解决。
近年来,国内外一些学者开始关注H7N9禽流感疫情传播模型的研究。陈永雪 [2] 考虑到H7N9禽流感病毒在禽类中有低致病性而在人类中具有高的致病性的情况,建立了一类总人口变化的SE-SIR人–禽H7N9禽流感模型,通过构造Lyapunov函数,利用Poincar-Bendixson定理、LaSalle不变性原理以及极限系统等理论研究了模型的全局动力学行为。此外,姜永 [3] ,段其琴 [4] ,陈娜 [5] ,胡新立 [6] [7] ,郭树敏 [8] 等人通过类似的方法,从H7N9禽流感的背景出发如考虑到药物治疗、媒体影响、感染途径等,建立了相应的禽流感模型并分析了其动力学行为。Iwami等人 [9] [10] 基于Li和Muldowney几何方法 [11] [12] 研究了一类病毒发生突变的人–禽流行病模型。陈永雪 [13] 也利用Li和Muldowney思想建立了一类H7N9病毒在人类中突变的禽流感模型。
上述文献针对禽流感自身的特点以及传播过程对模型进行了合理假设,建立相关模型,利用理论结果解释并评估了禽流感防控措施的效果。本文在上述文献基础上,考虑禽流感病毒在人类间的传播存在潜伏期的情形,进一步建立具有潜伏期的人–禽流行病模型。利用LaSalle不变性原理、Poincar-Bendixson定理以及改进的Li-Muldowney几何方法 [14] 对所建立的模型进行了动力学性态分析。
2. 预备知识
如下微分方程
(2.1)
其中 。设 是系统(2.1)的解,且 。
对系统(2.1)我们作如下基本假设:
(H1) 是单连通区域;
(H2) 存在一个紧吸收集 ;
(H3) 系统(2.1)在 中有唯一的平衡点 。
令 是 中一个 矩阵值函数,假设对 , 存在且连续。令
其中矩阵 是
且 是Jacobian矩阵 的二阶可加性复合矩阵。一般来说,对于 矩阵 , 是一个 矩阵。例如,当 时,有
.
在 中, 考虑矩阵 的Lozinskiĭ测度
.
定义量 为
Li-Muldowney [16] 指出若 是单连通,条件 排除了任何周期轨道的存在性,且他们给出了如下结论。
定理2.1 假设(H1)-(H3)成立,若 时,则系统(2.1)的唯一平衡点 在 中是全局渐近稳定的。
此外,吕贵臣和陆征一 [14] 基于时间平均性质,对定理2.1也做了推广,他们得到了如下结论。
定理2.2 若系统(2.1)满足条件(H1)-(H3),则系统(2.1)存在唯一的平衡点 在 中是全局渐近稳定的如果条件( )成立:
( ) 存在正实数 ,使得对所有的 ,
其中, 表示矩阵 中的项。
3. 一类SI-SEIR模型的分析
3.1. 模型的建立
H7N9型禽流感在禽类中有低致病性,禽类一般不发病或症状很轻,而在人类中却有高致病性。由于禽类是人类感染禽流感的来源,因而我们首先考虑禽流感在禽类间的传播。
把禽类分为易感禽类和携带病毒的禽类,分别用 , 表示 时刻易感禽类和携病毒类禽类的数量,记 为禽类总数,假设其传播过程为:

Figure 1. Transmission process diagram of avian influenza in poultry
图1. 禽类系统传播过程图
由此,我们可以写出其对应SI型ODB模型。
(3.1)
其中, 表示禽类的常数输入率; 表示禽类对易感禽类的传染率, 则表示具有禽流感病毒的受感染禽类在时间 的感染能力; 表示禽类自然死亡率; 表示禽类的因病死亡率,这里假定所有参数均为正数。
其次,考虑禽流感在人类间的传播,H7N9禽流感病毒主要通过带病毒的禽类与人类接触进行传播,目前并没有明显数据表明禽流感在人类中可以相互传播,对此,我们假设该病毒在人与人之间不存在传播。从禽流感病毒的背景出发,发现该病毒具有一周左右的潜伏期,因而我们假设其传播过程为:

Figure 2. Transmission process diagram of avian influenza in human
图2. 人类系统传播过程图
因此,对人类系统我们考虑SEIR模型。把人类分为易感者类、潜伏期者类、染病者类和移除者类,分别用 , , , 表示其在 时刻的人口数量,记 为 时刻人类总数,因而结合上述传播框图,建立如下SEIR模型:
(3.2)
其中,参数 表示人类的常数输入率; 表示人类和禽类接触时处于染病期的禽类对人类的传染率; 表示人类从潜伏者转化为染病者的转化率; 表示人类自然死亡率; 表示人类的因病死亡率; 表示人类的恢复率,这里假定所有参数均为正数。
综上,我们给出如下SI-SEIR人–禽流感模型。
(3.3)
3.2. 有界性
考虑疾病传播的生物学意义,设 由系统(3.3)可得
(3.4)
且可行域 。
定理3.1 如果 成立,那么系统(3.3)的所有解是最终一致有界的。
证明:由 可得
由比较定理得
故
即 最终一致有上界。
又
由比较原理得
故
即 最终一致有下界。
因此,存在充分大的 ,当 ,存在正常数 和 ,使得 。同理可得,存在充分大的 ,当 ,存在正常数 和 ,使得 。即结论得证。
3.3. 平衡点的稳定性分析
3.3.1. 禽类系统分析
由于禽类系统(3.1)与人类系统(3.2)是独立的,故首先考虑禽类系统。令系统(3.1)的右边为零,显然
它具有一个无病平衡点 ,其中 。记另一个平衡点为 ,其中 , 。
定义基本再生数 。在 中, 始终存在。当 时, 存在。且我们有:
定理3.2 如果 ,那么 在 上是全局渐近稳定的;如果 ,那么 在 上是全局渐近稳定的。
证明:设Lyapunov函数为 函数满足
易知,当 时, 平衡点 在 上是不稳定的;当 时, 。
显然, ,易知系统(3.1)在 中的最大不变集 只在集合 。由La Salle不变性原理 [15] 知,无病平衡点 在 上是全局渐近稳定的,且 。
下面考虑平衡点 。如果 , 在 上存在。系统(3.1)在 的Jacobian矩阵为
可知Jacobian矩阵 的特征方程为:
显然,若 ,则有 , 。即特征方程的根有负实部。故若 ,正平衡点 在 上是局部渐近稳定的。下证 在 上是全局渐近稳定的。
取Dulac函数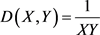 ,设
,设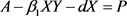 ,
,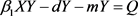 ,于是
,于是
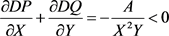
因而,系统(3.1)不存在周期解,由文献MC. and M [16] 中定理2.1知正平衡点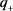 在
在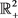 上是全局吸引的。故禽类系统的正平衡点
上是全局吸引的。故禽类系统的正平衡点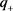 在
在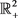 上是全局渐近稳定的。
上是全局渐近稳定的。
3.3.2. 禽类–人类系统分析
当 ,系统(3.3)有两个平衡点:无病平衡点
,系统(3.3)有两个平衡点:无病平衡点 和唯一的正平衡点
和唯一的正平衡点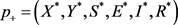 ,其中
,其中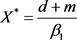 ,
,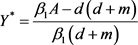 ,
,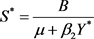 ,
,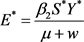 ,
, ,
,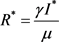 。
。
下面给出系统(3.3)的Jacobian矩阵

简单计算得, 对应的特征根分别为
对应的特征根分别为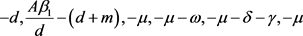 。显然,当
。显然,当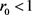 时,
时,
无病平衡点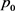 局部渐近稳定。类似地,
局部渐近稳定。类似地,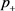 对应的特征根分别为
对应的特征根分别为
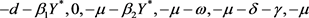 。由于该Jacobian矩阵的代数重数与几何重数相等,故当
。由于该Jacobian矩阵的代数重数与几何重数相等,故当 时,平衡点
时,平衡点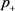 局部渐近稳定。因此,可以得到下面结论。
局部渐近稳定。因此,可以得到下面结论。
定理3.3 若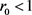 ,则
,则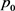 是局部渐近稳定的;若
是局部渐近稳定的;若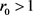 ,则
,则 不稳定而
不稳定而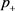 是局部渐近稳定的。
是局部渐近稳定的。
下面考虑系统(3.3)的无病平衡点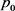 。定义
。定义

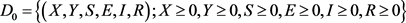
定理3.4 若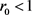 ,系统(3.3)的无病平衡点
,系统(3.3)的无病平衡点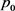 是全局渐近稳定的。
是全局渐近稳定的。
证明:当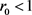 时,无病平衡点
时,无病平衡点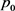 是局部渐近稳定的,且
是局部渐近稳定的,且
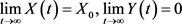 .
.
由定理3.2,结合极限系统 [17] 理论,知
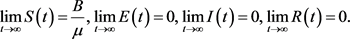
即系统(3.3)是全局吸引的。故当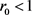 时,无病平衡点
时,无病平衡点 在
在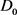 上是全局渐近稳定的。
上是全局渐近稳定的。
下面讨论系统(3.3)地方病平衡点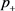 的全局稳定性。在给出主要结论之前,我们需要如下引理。
的全局稳定性。在给出主要结论之前,我们需要如下引理。
引理3.5 [18] 设
(A1)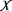 是
是 的一个紧子集;
的一个紧子集;
(A2)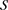 是
是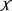 的一个紧子集。
的一个紧子集。
若存在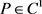 (
( ),使得
),使得
(1)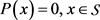 ;
;
(2)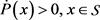 。
。
则存在常数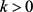 和充分大的
和充分大的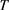 ,使得对任意的
,使得对任意的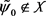 和任意的
和任意的 ,有
,有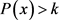 的一个紧子集;
的一个紧子集;
定理3.6 若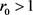 ,则系统(3.3)是永久生存的。
,则系统(3.3)是永久生存的。
证明:由定理3.1及定理3.4知,存在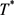 ,当
,当 时,存在
时,存在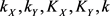 及
及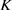 ,使
,使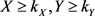 ,及
,及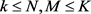 。定义
。定义
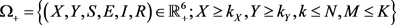
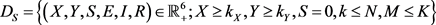
易知,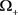 是
是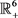 的紧子集,
的紧子集,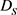 是
是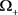 的紧子集,且
的紧子集,且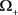 是前向不变的。
是前向不变的。
令 ,那么
,那么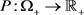 是
是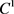 的,当且仅当
的,当且仅当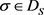 时有
时有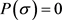 。此外,对任意
。此外,对任意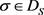 有
有 。因此,由引理3.5知,存在正常数
。因此,由引理3.5知,存在正常数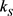 ,使得对任意
,使得对任意 有
有
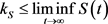 .
.
结合定理3.1知,存在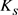 ,使
,使
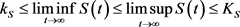 .
.
同理可得,存在 ,使
,使
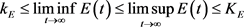
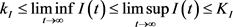
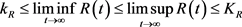
故系统(3.3)是永久生存的。
定理3.7若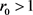 ,则
,则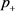 是全局渐近稳定的。
是全局渐近稳定的。
证明:由定理3.2知,当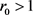 ,
, 时,
时,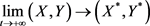 。又由定理3.6知,系统(3.3)是永
。又由定理3.6知,系统(3.3)是永
久生存的。由于人类系统的前三个方程中不含有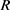 ,故系统(3.3)的全局稳定性可化为其对应的极限系统的研究:
,故系统(3.3)的全局稳定性可化为其对应的极限系统的研究:
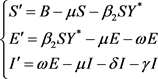 (3.5)
(3.5)
极限系统(3.5)在一般解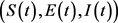 下的Jacobian矩阵为
下的Jacobian矩阵为
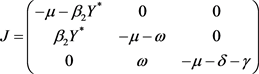 .
.
对应第二可加性复合矩阵为
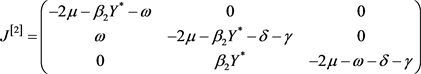 .
.
取函数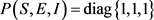 ,因此
,因此
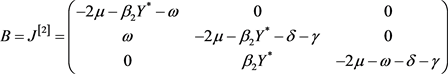 .
.
取向量范数 ,则
,则

由于
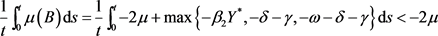
故

因此,由定理2.1,正平衡点 是全局渐近稳定的。
是全局渐近稳定的。
4. 结论
本文考虑了禽流感在传播过程中在人类中具有潜伏效应的一类H7N9流行病模型。通过对模型的分析可以知道,禽流感能否成为流行病取决于基本再生数是否大于1。当基本再生数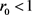 时,无病平衡点是渐近稳定的,且是全局渐近稳定的,疾病将会灭绝。当
时,无病平衡点是渐近稳定的,且是全局渐近稳定的,疾病将会灭绝。当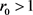 时,地方病平衡点是全局渐近稳定的,此时疾病将会成为流行病。
时,地方病平衡点是全局渐近稳定的,此时疾病将会成为流行病。
基金项目
国家自然科学基金资助(11401062),重庆市科委前沿与应用基础研究项目资助(cstc2014jcyjA00023)。
文章引用
赵亚飞,苏 强,吕贵臣. 具有潜伏效应的H7N9型禽流感模型的动力学分析
Dynamical Behaviors of the H7N9 Avian Influenza with Latent Period[J]. 应用数学进展, 2017, 06(08): 917-925. http://dx.doi.org/10.12677/AAM.2017.68110
参考文献 (References)
- 1. 中国疾病预防控制中心. 数据统计: 法定传染报告[EB/OL]. http://www.chinacdc.cn/tjsj_6693/fdcrbbg/, 2017-06-29.
- 2. Hutson, V. (1984) A Theorem on Average Liapunov Functions. Monatshefte für Mathematik, 98, 267-275. https://doi.org/10.1007/BF01540776
- 3. 陈永雪. 基于禽中低致病性的H7N9禽流感模型的动力学性质[J]. 生物数学学报, 2014(4): 627-634.
- 4. Jiang, Y. and Chen, Y. (2013) Dynamic Analysis of an Infec-tious Disease between Human and Poultry. Journal of Biomathematics, 4, 003.
- 5. 殷其琴, 冯光庭, 张兴安. 两类禽流感模型的动力学分析[J]. 应用数学, 2015, 28(3): 481-489.
- 6. 陈娜, 刘云芳, 朱思峰. 两类带有接种的H7N9禽流感模型[J]. 数学的实践与认识, 2016, 46(1): 162-169.
- 7. 胡新利, 杨亚莉, 赵惠文, 等. 媒体报道对禽流感(H7N9)传播影响的研究[J]. 西北大学学报自然科学版, 2014, 44(4): 525-528.
- 8. 胡新利, 刘艳, 陈瑶, 等. 具有饱和治疗率的H7N9 型禽流感模型的动力学性态分析[J]. 纺织高校基础科学学报, 2016, 29(3): 306-311.
- 9. 郭树敏, 李学志. 具有常数输入的H7N9 禽流感动力学模型分析[J]. 信阳师范学院学报: 自然科学版, 2017, 30(1): 13-16.
- 10. Iwami, S., Takeuchi, Y. and Liu, X. (2007) Avian-Human Influenza Epidemic Model. Mathematical Biosciences, 207, 1-25. https://doi.org/10.1016/j.mbs.2006.08.001
- 11. Eunok, J., Iwami, S., Takeuchi, Y., et al. (2009) Optimal Control Strategy for Prevention of Avian Influenza Pandemic. Journal of Theoretical Biology, 260, 220-229. https://doi.org/10.1016/j.jtbi.2009.05.031
- 12. Li, M.Y. and Muldowney, J.S. (1996) A Geometric Approach to Global-Stability Problems. SIAM Journal on Mathematical Analysis, 27, 1070-1083. https://doi.org/10.1137/S0036141094266449
- 13. Li, M.Y. and Wang, L. (2002) Global Stability in Some SEIR Epidemic Models, Mathematical Approaches for Emerging and Reemerging Infectious Diseases: Models, Methods, and Theory. Springer, New York, 295-311. https://doi.org/10.1007/978-1-4613-0065-6_17
- 14. Chen, Y. and Wen, Y. (2015) Global Dynamic Analysis of a H7N9 Avian-Human Influenza Model in an Outbreak Region. Journal of Theoretical Biology, 367, 180-188. https://doi.org/10.1016/j.jtbi.2014.12.002
- 15. Lu, G. and Lu, Z. (2017) Geometric Approach to Global Asymptotic Stability for the SEIRS Models in Epidemiology. Nonlinear Analysis: Real World Applications, 36, 20-43. https://doi.org/10.1016/j.nonrwa.2016.12.005
- 16. La Salle, J.P. (1976) The Stability of Dynamical Systems. CBMS-NSF Regional Conference Series in Applied Mathematics, 27, 1121-1130.
- 17. Li, M.Y. and Muldowney, J.S. (1995) Global Stability for the SEIR Model in Epidemiology. Mathematical Biosciences, 125, 155-164. https://doi.org/10.1016/0025-5564(95)92756-5
- 18. Thieme, H.R. (1992) Convergence Results and a Poinca-ré-Bendixson Trichotomy for Asymptotically Autonomous Differential Equations. Journal of Mathematical Biology, 30, 755-763. https://doi.org/10.1007/BF00173267