Advances in Applied Mathematics
Vol.07 No.04(2018), Article ID:24439,7
pages
10.12677/AAM.2018.74036
The First Integral Method for Solving Exact Solution of GDNLSE
Na Yang, Longwei Chen*
College of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan

Received: Mar. 29th, 2018; accepted: Apr. 12th, 2018; published: Apr. 20th, 2018

ABSTRACT
The first integral method is mainly adopted in this paper to study the nonlinear generalized Schrodinger equation with derivative. By introducing the traveling wave transformation, the original nonlinear generalized Schrodinger equation with derivative has been changed into an ordinary differential equation. Then according to the division theorem of polynomial, exact traveling wave solutions of the nonlinear generalized Schrodinger equation with derivative are obtained.
Keywords:The First Integral Method, Ordinary Differential Equation, Traveling Wave Solutions
基于首次积分法研究GDNLSE方程的精确解
杨娜,陈龙伟*
云南财经大学统计与数学学院,云南 昆明

收稿日期:2018年3月29日;录用日期:2018年4月12日;发布日期:2018年4月20日

摘 要
本文主要采用首次积分法对广义带导数的非线性Schrodinger方程进行研究,通过引入行波变换化简方程,将原广义带导数的非线性Schrodinger方程转化为常微分方程,再根据多项式的整除定理,得到广义带导数的非线性Schrodinger方程的精确行波解。
关键词 :首次积分法,常微分方程,行波解

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
关于非线性偏微分方程行波解的探讨在研究非线性物理现象中起着非常重要作用。而非线性偏微分方程的精确求解及其解法研究作为非线性科学中的前沿研究课题和热点问题,更是极具挑战性。近几年,求解非线性偏微分方程的方法得到了一定的发展,例如,F展开法 [1] 、齐次平衡法 [2] 、变量分离法 [3] 、tanh函数法 [4] 和Darboux变换法 [5] 等。利用这些方法求解了物理和力学中许多非常重要的非线性偏微分方程,不但获得了已有的结果,而且得到了许多新的结果,丰富和发展了非线性偏微分方程解法研究的内容。而首次积分法 [6] [7] 也是一种行之有效的求解非线性偏微分方程行波解的方法。
本文将利用首次积分法求解广义带导数的非线性Schrodinger方程精确解,方程如下:
(1)
其中 为实常数,而u是一个复函数。
2. 求解过程
2.1. 化简方程
作变换 , , 。其中 为实常数。将上式带入(1)式中,并
分离实部和虚部,整理可得到一个常微分方程组
(2)
为了求解方程(1)的非平凡解,我们需假设 且 ,于是,可以得到
(3)
为了计算简便,我们令 , , ,可以得到
(4)
2.2. 求解方程
下面引入新的变量 , ,则(4)式转化为
(5)
为了使用首次积分法,我们设
(6)
其中 是关于X的多项式。
由多项式的整除原理知,存在多项式 ,使得
(7)
2.2.1. 情况一
当 时,将(5)和(6)式带入到(7),并且由 的系数相等,对应 的系数,分别得到
(8)
(9)
(10)
由(8)式可知, 是常数, 。为方便起见,不妨设 。而由(9)式得 。又根据(10)式知 , 。设
(11)
由(9)式得
(12)
其中, 为积分常数。将 代入(10)式,由待定系数法,可得当 ,且
时,
(13)
将上式代入到(6)式中得
(14)
由(14)和(5)得
(15)
解常微分方程(15)得到
(16)
(17)
其中 为任意常数。
从而得到方程(1)的下列形式的精确解
(18)
(19)
2.2.2. 情况二
当 时,即
(20)
将(5)和(20)式代入(7)式,通过比较 的系数,对应 的系数,分别得到
(21)
(22)
(23)
(24)
因为 均是关于X的多项式,于是由(21)~(24)得: , , 。为方便起见,这里不妨设 。
下面分两种情况讨论 和 。
1) 当 时,由(22)和(24)知,满足条件。又由(23)知,
, 为任意常数。
将 代入(6)式得 。即
(25)
为计算方便,我们只讨论正号的情况,且设 ,则 ,那么上式变为
(26)
设 ,于是根据三次方程的判别式D及盛金公式,有以下几种情况:
a) 当 时,方程有一个三重根 ,则 ,
。那么此时, ,其中 为任意常数。而 ,
于是得到方程(1)下列形式的精确解
(27)
b) 当 时,方程有三个不相等的实根 ,于是 ,而 ,那么此时, ,其中 为任意常数, , 。
于是得到方程(1)下列椭圆函数形式的精确解
(28)
c) 当 时,方程有三个实根,其中有一个两重根,分别为 (为两重根)。于是
, ,此时, ,其中 为任意常数, 。
于是得到方程(1)以下指数函数形式的精确解
(29)
d) 当 时,方程有一个实根 和一对共轭虚根 。于是
,
,此时,
,其中
为任意常数,
,
, ,
, 。
。
于是得到方程(1)下列椭圆函数形式的精确解
 (30)
(30)
2) 当 时,只有当
时,只有当 时不会产生矛盾。不
时不会产生矛盾。不
妨设 ,那么
,那么 ,将其代入到(23)式得到
,将其代入到(23)式得到 ,其中
,其中 为积分常数。
为积分常数。
再将 代入(24)式,通过比较
代入(24)式,通过比较 的系数,借助Maple软件,可得
的系数,借助Maple软件,可得
a) ,且
,且 。
。
可以得出 ,
, ,代入(20)式得
,代入(20)式得 ,即
,即 ,解常微分方程可得
,解常微分方程可得 ,其中
,其中 为任意常数。从而得到方程(1)的以下形式的行波解
为任意常数。从而得到方程(1)的以下形式的行波解
 (31)
(31)
b) ,且
,且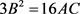 。
。
可以得出 ,
, ,代入(20)式得
,代入(20)式得 ,即
,即 ,解常微分方程可得
,解常微分方程可得 ,其中
,其中
 为任意常数。从而得到方程(1)的以下指数函数形式的行波解
为任意常数。从而得到方程(1)的以下指数函数形式的行波解
 (32)
(32)
c)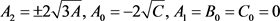 ,且
,且 。
。
可以得出 ,
,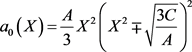 ,代入(20)式得
,代入(20)式得
 ,即
,即 ,解常微分方程可得
,解常微分方程可得 ,其中
,其中
 为任意常数。从而得到方程(1)的以下指数函数形式的行波解
为任意常数。从而得到方程(1)的以下指数函数形式的行波解
 (33)
(33)
3. 结论
本文我们利用首次积分法,根据m的不同情况进行讨论,对GDNLSE求精确解,得到了指数形式波解和其他形式的行波解等。另外,关于首次积分法中的m,本文只讨论了m = 1和m = 2两种情形。对于m = 3,甚至m更大的情形,我们没有讨论。m越大,求解会越复杂,甚至可能会导致无法求解。因此,进一步发展和完善首次积分法,将成为我们未来研究的课题。
文章引用
杨 娜,陈龙伟. 基于首次积分法研究GDNLSE方程的精确解
The First Integral Method for Solving Exact Solution of GDNLSE[J]. 应用数学进展, 2018, 07(04): 303-309. https://doi.org/10.12677/AAM.2018.74036
参考文献
- 1. 刘涛立. F-展开法研究[D]: [硕士学位论文]. 兰州: 兰州大学, 2004.
- 2. 杨攀攀. 齐次平衡法和非线性偏微分方程的孤立波解[D]: [硕士学位论文]. 南京: 南京理工大学, 2008.
- 3. Tang, X.Y. and Lou, S.Y. (2002) Abundant Structures of the Dispersive Long Wave Equation in (2 + 1)-Dimensional Spaces. Chaos, Solitons & Fractals, 14, 1451-1456. https://doi.org/10.1016/S0960-0779(02)00077-2
- 4. 徐振民. 推广的Tanh-函数法及其应用[J]. 广西民族大学学报(自然科学版), 2009, 3(15): 54-56.
- 5. 闵迪. 非线性发展方程的求解与达布变换[D]: [硕士学位论文]. 大连: 辽宁师范大学, 2010.
- 6. Li, H. and Guo, Y. (2006) New Exact Solutions to the Fitzhugh-Nagumo Equation. Applied Mathematics and Computation, 180, 524-528. https://doi.org/10.1016/j.amc.2005.12.035
- 7. Raslan, K.R. (2008) The First Integral Method for Solving Some Important Nonlinear Partial Differential Equations. Nonlinear Dynamics, 53, 281-286. https://doi.org/10.1007/s11071-007-9262-x
NOTES
*通讯作者。