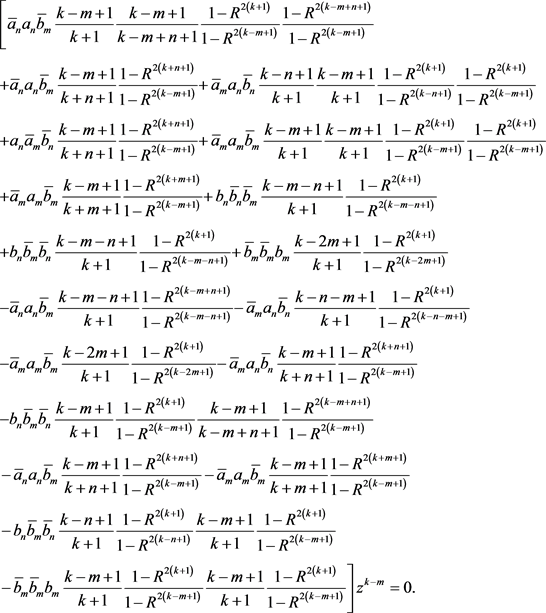圆环上以有界调和函数为符号的Toeplitz算子的拟正规性 Quasi-Normality of Toeplitz Operators with Bounded Harmonic Functions on Rings

doi:10.12677/AAM.2019.87138

Advances in Applied Mathematics
Vol. 08 No. 07 ( 2019 ), Article ID: 31112 , 7 pages
10.12677/AAM.2019.87138

Quasi-Normality of Toeplitz Operators with Bounded Harmonic Functions on Rings

Wei Shang, Shuning Cui, Huanran Wang

●How to Cite this Article

School of Mathematics, Liaoning Normal University, Dalian Liaoning

Email: 1025815700@qq.com

Received: Jun. 12^th, 2019; accepted: Jun. 25^th, 2019; published: Jul. 1^st, 2019

ABSTRACT

Functional space operator theory has always been an important branch of functional analysis. In this paper, we prove that there is the bounded harmonic function $u (z) = f (z) + \bar{g (z)}$ in the ring Bergman space, where Toeplitz operators with symbols of $f (z) = a_{n} z^{n} + a_{m} z^{m}$ , $g (z) = b_{n} z^{n} + b_{m} z^{m}$ (Where m and n are non-negative integers) must be normal if they are quasi-normal.

Keywords:Ring, Bergman Space, Toeplitz Operator, Quasi-Normality

圆环上以有界调和函数为符号的Toeplitz算子的拟正规性

尚巍，崔姝宁，王焕然

辽宁师范大学数学学院，辽宁大连

Email: 1025815700@qq.com

收稿日期：2019年6月12日；录用日期：2019年6月25日；发布日期：2019年7月1日

摘要

函数空间算子理论一直是泛函分析研究中的一个重要分支之一。本文证明了在圆环Bergman空间上以有界调和函数 $u (z) = f (z) + \bar{g (z)}$ ，其中以 $f (z) = a_{n} z^{n} + a_{m} z^{m}$ ， $g (z) = b_{n} z^{n} + b_{m} z^{m}$ (其中m，n是非负整数)为符号的Toeplitz算子若是拟正规性，则一定是正规的.

关键词 :圆环，Bergman空间，Toeplitz算子，拟正规性

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

关于函数空间上以有界调和函数为符号的Toeplitz算子拟正规性的研究，主要集中在Hardy空间上。Amemiya [1] 等，证明了Hardy空间上以本性有界可测函数为符号的拟正规Toeplitz算子 $T_{φ}$ 要么是正规的要么是解析的。Ito和Wong证明了在Hardy空间上，设 $φ$ 是一有界解析函数,若 $T_{φ}$ 是拟正规的，则 $φ$ 是一内函数的常数倍 [2] ，但是作者又考虑了“almost”有界解析函数 $φ$ ，若 $T_{φ}$ 是拟正规的，则 $φ$ 是一内函数的常数倍，或 $φ$ 是一非解析三角多项式，且在这种情况下 $T_{φ}$ 是正规的。在Bergman空间上，Faour证明了拟正规与正规算子的关系： $ψ$ 为开单位圆盘上的有界解析函数， $λ$ 为一复数，且 $ϕ = ψ + λ \bar{ψ}$ ，如果 $T_{ϕ}$ 是拟正规的，则 $T_{ϕ}$ 是正规的 [3] 。

2. 预备知识

2.1. Bergman空间上的Toeplitz算子相关知识

记C是复平面， $0 < R < 1$ ，定义 $Ω = {z \in C : R < | z | < 1}$ 。 $d A (z) = \frac{r}{π} d r d θ = \frac{1}{π} d x d y$ 为C上的Lebesgue

测度。 $L^{2} (Ω)$ 是 $Ω$ 上关于 $d A$ 平方可积的可测函数全体构成的Hilbert空间，Bergman空间 $L_{a}^{2} (Ω)$ 为 $L^{2} (Ω)$ 上由全体解析函数构成的闭子空间，即

$L_{a}^{2} (Ω) = {f : f 为解析函数且 \int_{Ω} {| f (z) |}^{2} d A (z) < + \infty} .$

对任意的 $f, g \in L^{2} (Ω)$ ，在 $L^{2} (Ω)$ 空间中内积为：

$〈 f, g 〉 = \int_{Ω} f (z) \bar{g (z)} d A (z) .$

P是从 $L^{2} (Ω)$ 到 $L_{a}^{2} (Ω)$ 的正交射影，对任意的 $z, ω \in Ω$ ，圆环 $Ω$ 上的再生核定义为：

$K_{z} (ω) = \sum_{\begin{array}{l} n \neq - 1 \\ n = - \infty \end{array}}^{+ \infty} \frac{n + 1}{1 - R^{2 (n + 1)}} {(ω \bar{z})}^{n} - \frac{1}{2 \log R} {(ω \bar{z})}^{- 1},$

定义 $k_{ω} = \frac{K_{ω}}{‖ K_{ω} ‖}$ 为正规化的再生核。则对任意的 $f \in L_{a}^{2} (Ω)$ ，

$P f (z) = 〈 f, K_{z} 〉 (z \in Ω) .$

本文记 $L^{\infty} (Ω)$ 为由在 $Ω$ 上关于 $d A$ 的本性有界可测函数构成的Banach空间。

定义1.1设 $φ \in L^{\infty} (Ω)$ ，以 $φ$ 为符号的Toeplitz算子有以下定义：

$T_{φ} f = P (φ f), f \in L_{a}^{2} (Ω) .$

以 $φ$ 为符号的Hankel算子的定义是：

$H_{φ} f = (I - P) (φ f), f \in L_{a}^{2} (Ω) .$

其中，I为 $L^{2} (Ω)$ 上的恒等算子。

关于Bergman空间上Toeplitz算子的性质在文献 [4] 中有详细说明。类似于圆盘上的Bergman空间上的Toeplitz算子，以下列出本文用到的Toeplitz算子的性质：

1) $T_{φ}^{*} = T_{\bar{φ}}$ ；

2) 若 $a, b$ 是任意复数，则 $T_{a ψ + b φ} = a T_{ψ} + b T_{φ}$ ；

3) 若 $φ$ 是解析函数，则 $T_{φ} f = φ f$ ， $f \in L_{a}^{2} (Ω)$ ，

其中 $φ, ψ \in L^{\infty} (Ω)$ 。

2.2. Bergman空间上的正规、拟正规Toeplitz算子相关知识

以下给出Hilbert空间上正规算子、拟正规算子和亚正规算子的定义。

定义1.2 设 $T \in B (H)$ ，若 $T^{*} T = T T^{*}$ ，称T为正规算子。

正规算子是线性代数中正规矩阵的概念在无穷维Hilbert空间上的推广。

定义1.3 设 $T \in B (H)$ ，若 $T T^{*} T = T^{*} T T$ ，称T为拟正规算子。

若T是正规的，则 $T T^{*} T = (T T^{*}) T = (T^{*} T) T = T^{*} T T$ ，即T是拟正规的。

3. 主要结果

本部分主要研究圆环Bergman空间 $L_{a}^{2} (Ω)$ 上的拟正规Toeplitz算子。

引理2.1设 $k, m$ 是非负整数，

$T_{{\bar{z}}^{m}} z^{k} = {\begin{cases} \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} z^{k - m} k - m \neq - 1 \\ - \frac{(1 - R^{k + m + 1})}{(k + m + 1) \log R} z^{- 1} k - m = - 1 \end{cases}$

证明：设 $z = r e^{i θ} \in Ω$ ，则

$T_{{\bar{z}}^{m}} z^{k} (ω) = P ({\bar{z}}^{m} z^{k}) (ω) = 〈 z^{k} {\bar{z}}^{m}, K_{ω} (z) 〉$

代入

$K_{ω} (z) = \sum_{\begin{array}{l} n \neq - 1 \\ n = - \infty \end{array}}^{+ \infty} \frac{n + 1}{1 - R^{2 (n + 1)}} {(\bar{ω} z)}^{n} - \frac{1}{2 \log R} {(\bar{ω} z)}^{- 1},$

$\begin{matrix} T_{{\bar{z}}^{m}} z^{k} = \sum_{\begin{array}{l} p \neq - 1 \\ p = - \infty \end{array}}^{\infty} \frac{p + 1}{1 - R^{2 (p + 1)}} ω^{p} 〈 {\bar{z}}^{m} z^{k}, z^{p} 〉 - \frac{1}{2 \log R} ω^{- 1} 〈 {\bar{z}}^{m} z^{k}, z^{- 1} 〉 \\ = \frac{1}{π} \sum_{\begin{array}{l} p \neq - 1 \\ p = - \infty \end{array}}^{\infty} \frac{p + 1}{1 - R^{2 (p + 1)}} ω^{p} \int_{0}^{2 π} \int_{R}^{1} r^{k + m + p + 1} e^{i (k - m - p) θ} d r d θ \\ - \frac{1}{2 π \log R} ω^{- 1} \int_{0}^{2 π} \int_{R}^{1} r^{k + m} e^{i (k - m + 1) θ} d r d θ \end{matrix}$

由

${\begin{cases} \int_{0}^{2π} e^{i (n - l) θ} d θ = 2 π, n = l; \\ \int_{0}^{2π} e^{i (n - l) θ} d θ = 0, n \neq l . \end{cases}$

进行如下讨论：

① 当 $k \neq m - 1, k - m - p = 0$ 时， $p = k - m$ 时， $P (z^{k} {\bar{z}}^{m}) (ω) = \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} ω^{k - m}$ ；

② 当 $k = m - 1$ 时， $k - m - p \neq 0 (p \neq - 1)$ ，则 $P (z^{k} {\bar{z}}^{m}) (ω) = - \frac{(1 - R^{k + m + 1})}{(k + m + 1) \log R} ω^{- 1}$ 。

以下定理证明圆环Bergman空间上以有界调和函数为符号的Toeplitz算子的交换性。

定理2.1设 $φ = f_{1} + {\bar{f}}_{2}$ ， $ψ = g_{1} + {\bar{g}}_{2}$ 在 $Ω$ 上是有界调和函数。则 $T_{φ} T_{ψ} = T_{ψ} T_{φ}$ 成立的充要条件是：

1) $φ$ 和 $ψ$ 在 $Ω$ 上都是解析的。

2) $\bar{φ}$ 和 $\bar{ψ}$ 在 $Ω$ 上都是解析的。

3) 存在不同时为零的复常数a和b，则 $a φ + b ψ$ 在 $Ω$ 上也是常值函数。

根据定理2.1可得出以下推论。

推论2.1设 $u (z) = f (z) + \bar{g (z)}$ ， $T_{u}$ 为正规算子当且仅当 $a f + b g \equiv c$ 。其中c为常数，且 $| a | + | b | > 0$ 。

以下证明本章的主要定理，给出了拟正规Toeplitz算子与正规Toeplitz算子的关系。

定理2.2设 $u (z) = f (z) + \bar{g (z)}$ ， $f (z) = a_{n} z^{n} + a_{m} z^{m}$ ， $g (z) = b_{n} z^{n} + b_{m} z^{m}$ 若 $T_{u}$ 是拟正规的，则

$a_{n} = λ b_{n}, a_{m} = λ b_{m} (| λ | = 1),$

其中m, n是非负整数且 $n < m, a_{i} \neq 0, b_{j} \neq 0$ 且 $i, j = 1, 2$ 。

进而由推论2.1得 $T_{u}$ 为正规算子。

证明：对充分大的k，

$T_{u} z^{k} = T_{f + \bar{g}} z^{k} = T_{f} z^{k} + T_{\bar{g}} z^{k} = (f + T_{\bar{g}}) z^{k} .$

由引理2.1得，

$\begin{matrix} T_{u} z^{k} = a_{n} z^{k + n} + a_{m} z^{k + m} + {\bar{b}}_{n} \frac{k - n + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - n + 1)}} z^{k - n} \\ + {\bar{b}}_{m} \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} z^{k - m} \end{matrix}$

由此表达式可以看出， $T_{u} z^{k}$ 由四个单项式 $z^{k + n}, z^{k + m}, z^{k - n}, z^{k - m}$ 组成。每经 $T_{u}$ 作用一次，即被 $a_{n} z^{n},$ $a_{m} z^{m}, {\bar{b}}_{n} T_{{\bar{z}}^{n}}, {\bar{b}}_{m} T_{{\bar{z}}^{m}}$ 作用一次。因为 $k + 2 m - n$ 可以分解成：

$(k + m) + m + (- n), (k - n) + m + m, (k + m) - n + m .$

所以 $T_{\bar{u}} T_{u} T_{u} z^{k}$ 的表达式中 $z^{k + 2 m - n}$ 的系数为：

$\begin{array}{l} a_{m} a_{m} {\bar{a}}_{n} \frac{k + 2 m - n + 1}{k + 2 m + 1} \frac{1 - R^{2 (k + 2 m + 1)}}{1 - R^{2 (k + 2 m - n + 1)}} + a_{m} {\bar{b}}_{n} b_{m} \frac{k - n + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - n + 1)}} \\ + b_{m} {\bar{b}}_{n} a_{m} \frac{k + m - n + 1}{k + m + 1} \frac{1 - R^{2 (k + m + 1)}}{1 - R^{2 (k + m - n + 1)}} . \end{array}$ (1)

同理 $T_{u} T_{\bar{u}} T_{u} z^{k}$ 的表达式中 $z^{k + 2 m - n}$ 的系数为：

$\begin{array}{l} a_{m} a_{m} {\bar{a}}_{n} \frac{k + m - n + 1}{k + m + 1} \frac{1 - R^{2 (k + m + 1)}}{1 - R^{2 (k + m - n + 1)}} + a_{m} {\bar{b}}_{n} b_{m} \frac{k - n + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - n + 1)}} \\ + b_{m} {\bar{b}}_{n} a_{m} \frac{k + 2 m - n + 1}{k + 2 m + 1} \frac{1 - R^{2 (k + 2 m + 1)}}{1 - R^{2 (k + 2 m - n + 1)}} . \end{array}$ (2)

由 $T_{u} T_{u}^{*} T_{u} z^{k} = T_{u}^{*} T_{u} T_{u} z^{k}$ ，左右两边z的各项幂次相同。故(3.1)与(3.2)相同，合并同类项为

$[a_{m} (a_{m} {\bar{a}}_{n} - b_{m} {\bar{b}}_{n}) (\frac{k + 2 m - n + 1}{k + 2 m + 1} \frac{1 - R^{2 (k + 2 m + 1)}}{1 - R^{2 (k + 2 m - n + 1)}} - \frac{k + m - n + 1}{k + m + 1} \frac{1 - R^{2 (k + m + 1)}}{1 - R^{2 (k + m - n + 1)}})] z^{k + 2 m - n} = 0$

而

$a_{m} \neq 0$ ， $\frac{k + 2 m - n + 1}{k + 2 m + 1} \frac{1 - R^{2 (k + 2 m + 1)}}{1 - R^{2 (k + 2 m - n + 1)}} - \frac{k + m - n + 1}{k + m + 1} \frac{1 - R^{2 (k + m + 1)}}{1 - R^{2 (k + m - n + 1)}}$ 不恒为0,

得

$a_{m} {\bar{a}}_{n} = b_{m} {\bar{b}}_{n} .$

另一方面， $k - m$ 可以分解成：

$(k - n) + n - m, (k - n) - m + n, (k + m) - m - m,$

$(k + n) - m - n, (k + n) - n - m, (k - m) + n - n,$

$(k - m) + m - m, (k - m) - n + n, (k - m) - m + m,$

$(k - n) - m + n, (k - n) + n - m, (k + m) - m - m,$

$(k + n) - n - m, (k + n) - m - n, (k - m) - m + m,$

$(k - m) - n + n, (k - m) + m - m, (k - m) + n - n .$

所以 $T_{\bar{u}} T_{u} T_{u} z^{k}$ 的表达式中 $z^{k - m}$ 的系数为：

$\begin{array}{l} {\bar{a}}_{n} a_{n} {\bar{b}}_{m} \frac{k - m + 1}{k + 1} \frac{k - m + 1}{k - m + n + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} \frac{1 - R^{2 (k - m + n + 1)}}{1 - R^{2 (k - m + 1)}} \\ + {\bar{a}}_{n} a_{n} {\bar{b}}_{m} \frac{k - m + 1}{k + n + 1} \frac{1 - R^{2 (k + n + 1)}}{1 - R^{2 (k - m + 1)}} \\ + {\bar{a}}_{m} a_{n} {\bar{b}}_{n} \frac{k - n + 1}{k + 1} \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - n + 1)}} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} \\ + a_{n} {\bar{a}}_{m} {\bar{b}}_{n} \frac{k - m + 1}{k + n + 1} \frac{1 - R^{2 (k + n + 1)}}{1 - R^{2 (k - m + 1)}} \\ + {\bar{a}}_{m} a_{m} {\bar{b}}_{m} \frac{k - m + 1}{k + 1} \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} \\ + {\bar{a}}_{m} a_{m} {\bar{b}}_{m} \frac{k - m + 1}{k + m + 1} \frac{1 - R^{2 (k + m + 1)}}{1 - R^{2 (k - m + 1)}} \\ + b_{n} {\bar{b}}_{n} {\bar{b}}_{m} \frac{k - m - n + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m - n + 1)}} \\ + b_{n} {\bar{b}}_{m} {\bar{b}}_{n} \frac{k - m - n + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m - n + 1)}} \\ + {\bar{b}}_{m} {\bar{b}}_{m} b_{m} \frac{k - 2 m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - 2 m + 1)}} . \end{array}$

同理 $T_{u} T_{\bar{u}} T_{u} z^{k}$ 的表达式中 $z^{k - m}$ 的系数为：

$\begin{array}{l} {\bar{a}}_{n} a_{n} {\bar{b}}_{m} \frac{k - m - n + 1}{k + 1} \frac{1 - R^{2 (k - m + n + 1)}}{1 - R^{2 (k - m - n + 1)}} + {\bar{a}}_{m} a_{n} {\bar{b}}_{n} \frac{k - n - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - n - m + 1)}} \\ + {\bar{a}}_{m} a_{m} {\bar{b}}_{m} \frac{k - 2 m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - 2 m + 1)}} + {\bar{a}}_{m} a_{n} {\bar{b}}_{n} \frac{k - m + 1}{k + n + 1} \frac{1 - R^{2 (k + n + 1)}}{1 - R^{2 (k - m + 1)}} \\ + b_{n} {\bar{b}}_{m} {\bar{b}}_{n} \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} \frac{k - m + 1}{k - m + n + 1} \frac{1 - R^{2 (k - m + n + 1)}}{1 - R^{2 (k - m + 1)}} \\ + {\bar{a}}_{n} a_{n} {\bar{b}}_{m} \frac{k - m + 1}{k + n + 1} \frac{1 - R^{2 (k + n + 1)}}{1 - R^{2 (k - m + 1)}} + {\bar{a}}_{m} a_{m} {\bar{b}}_{m} \frac{k - m + 1}{k + m + 1} \frac{1 - R^{2 (k + m + 1)}}{1 - R^{2 (k - m + 1)}} \\ + b_{n} {\bar{b}}_{m} {\bar{b}}_{n} \frac{k - n + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - n + 1)}} \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} \\ + {\bar{b}}_{m} {\bar{b}}_{m} b_{m} \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} \frac{k - m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - m + 1)}} . \end{array}$

故 $T_{\bar{u}} T_{u} T_{u} z^{k}$ 的表达式中 $z^{k - m}$ 与 $T_{u} T_{\bar{u}} T_{u} z^{k}$ 的表达式中 $z^{k - m}$ 系数，合并同类项的式子为：

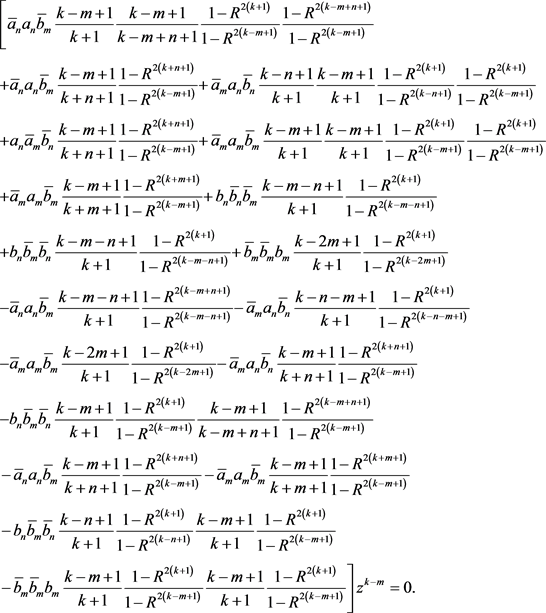
将 $a_{m} {\bar{a}}_{n} = b_{m} {\bar{b}}_{n}$ ，代入合并同类项，得：

$\begin{array}{l} [({| a_{n} |}^{2} - {| b_{n} |}^{2}) (\frac{k - 2 n + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - 2 n + 1)}} - \frac{{(k - m - 1)}^{2}}{(k - m + n + 1) (k + 1)} \frac{[1 - R^{2 (k + 1)}] [1 - R^{2 (k - m + n + 1)}]}{{[1 - R^{2 (k - m - 1)}]}^{2}}) \\ + ({| a_{m} |}^{2} - {| b_{m} |}^{2}) (\frac{k - 2 m + 1}{k + 1} \frac{1 - R^{2 (k + 1)}}{1 - R^{2 (k - 2 m + 1)}} - \frac{{(k - m + 1)}^{2}}{(k + 1)} \frac{1 - R^{2 (k + 1)}}{{[1 - R^{2 (k + n + 1)}]}^{2}})] z^{k - m} = 0. \end{array}$ (3.3)

故

当k充分大时，有

$| a_{m} | = | b_{m} | .$

对于 $z^{k - n}$ 前面的系数同理可得，

$| a_{n} | = | b_{n} | .$

记 $a_{n} = e^{i θ_{1}} b_{n}$ ， $a_{m} = e^{i θ_{2}} b_{m}$ $(0 \leq θ_{1}, θ_{2} < 2 π)$ 。又 $a_{m} {\bar{a}}_{n} = b_{m} {\bar{b}}_{n}$ ，故 $e^{i (θ_{2} - θ_{1})} b_{m} {\bar{b}}_{n} = b_{m} {\bar{b}}_{n}$ ，

即 $θ_{1} = θ_{2}$ 。即存在 $λ$ ， $| λ | = 1$ 。使得 $a_{n} = λ b_{n}, a_{m} = λ b_{m} .$

故 $f (z) = a_{n} z^{n} + a_{m} z^{m} = λ g (z)$ ，由推论2.1得 $T_{u}$ 为正规算子。

说明：上述证明中分解对应的单项式已被逐项验证。但由于篇幅限制，本文不一一列出。

4. 结论

关于Bergman空间上的拟正规Toeplitz算子的研究，主要都集中在圆盘上或者单连通区域上。本章考虑了将圆盘等单连通区域推广到圆环上，从而研究了圆环的Bergman空间上的Toeplitz算子的拟正规性问题，证明了以有界调和函数 $u (z) = f (z) + \bar{g (z)}$ ，其中 $f (z) = a_{n} z^{n} + a_{m} z^{m}$ ， $g (z) = b_{n} z^{n} + b_{m} z^{m}$ (其中m，n是非负整数)为符号的Toeplitz算子若是拟正规性，则一定是正规的。

本文遇到的困难之处是后期的多项式对应及得出结论过程需要很多计算。本章结论仅仅对四项多项式成立，如若推广到一般调和多项式，则计算量更大，结论也未知。进一步研究拟正规的Toeplitz算子与正规Toeplitz算子之间的问题会有更大意义。

文章引用

尚巍,崔姝宁,王焕然. 圆环上以有界调和函数为符号的Toeplitz算子的拟正规性
Quasi-Normality of Toeplitz Operators with Bounded Harmonic Functions on Rings[J]. 应用数学进展, 2019, 08(07): 1201-1207. https://doi.org/10.12677/AAM.2019.87138

参考文献

1. Amemiya, I., Ito, T. and Wong, T.K. (1975) On Quasinormal Toeplitz Operators. Proceedings of the American Math-ematical Society, 50, 254-258. https://doi.org/10.2307/2040549

2. Ito, T. and Wong, T.K. (1972) Subnormality and Quasinormality of Toeplitz Operators. Proceedings of the American Mathematical Society, 34, 157-164. https://doi.org/10.2307/2037918

3. Faour, N. (1989) On Quasinormal Subnormal and Hyponormal Toeplitz Operators. The Rendiconti del Circolo Matematico di Palermo, 38, 121-129. https://doi.org/10.1007/BF02844854

4. Zhu, K.H. (1961) Operayor Theory in Function Spaces. American Mathematical Society, Providence, RI, USA.

期刊菜单