Advances in Applied Mathematics
Vol.
09
No.
01
(
2020
), Article ID:
33701
,
11
pages
10.12677/AAM.2020.91001
Conservation Laws of the Defocusing Hirota Equation under Non-Zero Background
Qing Xu
School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Dec. 5th, 2019; accepted: Dec. 23rd, 2019; published: Dec. 30th, 2019

ABSTRACT
The conservation laws are important indexes for the integrability of nonlinear equations. It plays an important role in the research of partial differential equation systems. Based on Lax pair, this paper studies infinite conservation laws and higher-order conserved quantities of the one-dimensional defocusing Hirota equation under non-zero backgrounds.
Keywords:Hirota Equation, Lax Pair, Conservation Laws

散焦HIROTA方程在非零背景下的无穷守恒律
许庆
华南理工大学数学学院,广东 广州

收稿日期:2019年12月5日;录用日期:2019年12月23日;发布日期:2019年12月30日

摘 要
守恒律是非线性方程可积的一个重要指标,在偏微分方程系统的研究中扮演着重要的角色。本文基于Lax对,研究了一维散焦Hirota方程在非零背景下的无穷守恒律及其高阶守恒量。
关键词 :Hirota方程,Lax对,守恒律

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 问题背景及主要结论
随着现代科学的发展,线性微分方程已经无法确切的描述现实社会中各种现象出现的个体内在关系,随之而来的,非线性科学得以快速的发展,并在数学、物理、流体等领域中广泛应用。也正源于此,越来越多科学家投身到非线性偏微分方程的研究之中,并取得巨大的成就。而在这之间,数学家发现许多具有广泛应用背景的方程如:KdV方程、Schrödinger方程、sine-Gordon方程等都存在孤立子解,于此,孤立子理论得以产生并迅速发展。同时,因为光孤子在光纤通信中的重要作用,也使得众多的数学家开始致力于描述光孤子运动的非线性发展方程的研究,而这其中最具有代表性的方程就是Hirota方程。
广义的Hirota方程如下:
。 (1.1)
针对广义的Hirota方程,Poresezian [1] 、田播 [2] 等人分别利用Bäcklund、Hirota双线性方法得出了方程的孤子解,并分析了该孤子解的性质。而当方程(1.1)中系数
时候,方程就退化为广义的非线性Schrödinger方程:
。 (1.2)
该方程对于描述连续极限条件下不同磁性相互作用的动力学特性具有明显的效果,该Schrödinger方程的Lax对在 [3] 文献中也已经给出。当方程(1.1)中系数
,方程(1.1)就变成了变系数Hirota方程:
。 (1.3)
方程(1.3)的可积性在文献 [4] 中给出,同时,Radhakrishnan等人 [5] 利用Hirota双线性方法得出了该方
程的孤子解。当方程(1.1)中系数
,得到方程:
。 (1.4)
对式子(1.4)作坐标变换:
,即可得到方程:
。 (1.5)
相似于方程(1.5),本文深入研究了下列一维Hirota方程:
。 (1.6)
其中:
,。这是一个散焦立方非线性方程,包括三阶色散项和非线性色散项。守恒律反映了某物理量不随时间改变的一种现象。而在孤子理论中,人们发现这样一个事实,如果非线性发展方程具有孤立子解,那么几乎也具有无穷守恒律。因此,就一个孤子系统而言,寻找其无穷守恒律,对于证明此系统的可积性,甚至在证明其适定性方面有重大意义。下面我们将基于Lax对 [6],来研究散焦Hirota方程(1.6)在非零背景下的无穷守恒律及其高阶守恒量。
定义1.1 [7] 给定一般的非线性偏微分方程:
, (1.7)
其中:
是关于x和t的函数,而
是
及其导数的函数。若存在一对连续可微函数
和
,使得u按照方程(1.7)发展时候满足关系
, (1.8)
则称此关系式为式(1.7)的守恒律,而
和
分别称为守恒密度与连带流。
如果当
趋于无穷时,密度与流充分快地趋于零,则将守恒律在整个数轴上对x积分得:
,(1.9)
则积分
与时间t无关,是方程(1.7)的守恒量。
注:设二阶矩阵
,
我们定义如下符号意义:
。
定理1.1 HIROTA方程(1.6)具有无穷守恒律。
推论1.1 已知方程(1.6),则有
。 (1.10)
是其高阶守恒量。
2. 定理的证明
为了证明定理1.1,参考 [7] 中第三章内容和文献 [8] [9] 中孤立子理论,首先需要推导出方程(1.6)所对应的Lax对,而方程(1.6)可以由方程
。 (2.1)
作坐标变换得到,则首先可以研究方程(2.1)的Lax对。
命题2.1方程(2.1)对应的Lax对为:
, (2.2)
。 (2.3)
其中:
。
证明 我们假设方程(2.1)对应的Lax对具有如下形式:
。
为复平面上关于
的亚纯函数。因为
,则有
。
定义运算符:
,则
。
下面,我们对比
的系数:
(2.4)
(2.5)
(2.6)
(2.7)
。 (2.8)
根据式(2.4),并选择
, 其中
是常数。再根据式(2.5),则得到:
。
根据式(2.6),并选择
, 其中
是常数。则有
,。
根据式(2.7),并选择
, 则
。 (2.9)
求解式(2.9),可得
。
根据式子(2.8),并令
,则
。 (2.10)
求解式(2.10),可得
。
又根据
得到
。 (2.11)
将
代入式(2.11),得到
。 (2.12)
令
,,则可以得到:
。 (2.13)
综合以上,根据已得:
的值,可得式子(2.1)的Lax对。
命题2.2 方程(1.6)对应的Lax对为:
, (2.14)
。 (2.15)
其中
,
,
。
证明 根据式子(1.6)和(2.1)之间的坐标变换,易证。
命题2.3已知方程(1.6)的Lax对,在特殊解为
的情况下,方程有如下形式的基本解
,
其中:
,,。
证明 利用命题2.2的Lax对,有
引入算子
,作变换:
。则
。
利用线性代数可得到矩阵的对角化形式
。
引入
,则
。 (2.16)
同理,由于方程满足定命题2.2中lax对,关于参数t,亦可以得到:
。 (2.17)
结合式(2.16)和式(2.17)可以得到
。
继而
。
定理1.1的证明 根据命题2.2,我们知道方程(1.6)的Lax对。设
。
根据式(2.14),得到
。 (2.18)
继而利用式(2.18),得到
和
。 (2.19)
假设
,,将其带入式(2.19),得到
。
和
。
下面,我们比较
同次幂的系数,则得到:
。
根据同阶系数相等,可以算出
,下面列出前五个系数
,
和
。
根据命题2.3中得到的基本解的形式,假设
,其中
为关于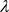 的解
的解
析函数。则
。
则有
。 (2.20)
已知
为关于
解析函数,且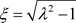 ,下面分析公式(2.20)右边部分,对
关于
展开,并合并 的同阶系数,则
,下面分析公式(2.20)右边部分,对
关于
展开,并合并 的同阶系数,则
。 (2.21)
同样,利用式(2.15)有
。(2.22)
根据式(2.22),有
。
其中:
。
综合以上,我们得到
的关于
的二阶微分
。
由
,则有
。
根据相容性条件
,可得到AKNS方程族的守恒律。
当
,即k为奇数时,
。 (2.23)
当
,即k为偶数时,
。 (2.24)
结合公式(2.23)和公式(2.24),下面列出其中两个守恒律
, (2.25)
。 (2.26)
推论1.1的证明 根据定理1.1,我们知道方程(1.6)的无穷守恒律如公式(2.23)和(2.24)所示。
根据式(2.26)得出守恒量
。 (2.27)
根据式(2.25)得出守恒量
。 (2.28)
则根据上面两个守恒量,我们得出
。 (2.29)
意义:文献 [10] [11] 在证明解的轨道稳定性时,利用了高阶守恒量,但未给出证明,本文给出了基于Lax对证明方程无穷守恒律和高阶守恒量的方法。此外,该部分内容为我们进一步利用无约束变分的方法研究方程:
。
的暗孤子解:
的轨道稳定性奠定了基础。
文章引用
许 庆. 散焦HIROTA方程在非零背景下的无穷守恒律
Conservation Laws of the Defocusing Hirota Equation under Non-Zero Background[J]. 应用数学进展, 2020, 09(01): 1-11. https://doi.org/10.12677/AAM.2020.91001
参考文献
- 1. Porsezian, K., Daniel, M. and Bharathikannan, R. (1991) Generalized -Dependent Hirota Equation: Singularity Structure, Bäcklund Transformation and Soliton Solutions. Physics Letters A, 156, 206-210.
https://doi.org/10.1016/0375-9601(91)90140-4
- 2. Wang, P., Tian, B., Liu, W.J., Li, M. and Sun, K. (2010) Soliton Solutions for a Generalized Inhomogeneous Variable-Coefficient Hirota Equation with Symbolic Computation. Studies in Applied Mathematics, 125, 213-222.
https://doi.org/10.1111/j.1467-9590.2010.00486.x
- 3. Porsezian, K. and Lakshmanan, M. (1991) On the Dynamics of the Radially Symmetric Heisenberg Ferromagnetic Spin System. Journal of Mathematical Physics, 32, 2923.
https://doi.org/10.1063/1.529086
- 4. Mahalingam, A. and Porsezian, K. (2001) Propagation of Dark Solitons with Higher-Order Effects in Optical Fibers. Physical Review E, 64, Article ID: 046608.
https://doi.org/10.1103/PhysRevE.64.046608
- 5. Radhakrishnan, R. and Lakshmanan, M. (1996) Exact Soliton Solutions to Coupled Nonlinear Schrödinger Equations with Higher-Order Effects. Physical Review E, 54, 2949.
https://doi.org/10.1103/PhysRevE.54.2949
- 6. Lax, P.D. (1968) Integrals of Nonlinear Equations of Evolution and Solitary Waves. Communications on Pure and Applied Mathematics, 21, 467-490.
https://doi.org/10.1002/cpa.3160210503
- 7. 陈登远. 孤子引论[M]. 北京: 科学出版社, 2006.
- 8. 郭柏灵, 庞小峰. 孤立子[M]. 北京: 科学出版社, 1987.
- 9. 谷超豪, 胡和生, 周子翔. 孤立子理论中的达布变换及其几何应用[M]. 上海: 上海科学技术出版社, 1999.
- 10. Grillakis, M., Shatah, J. and Strauss, W. (1987) Stability Theory of Solitary Waves in the Presence of Symmetry I. Journal of Functional Analysis, 74, 160-197.
https://doi.org/10.1016/0022-1236(87)90044-9
- 11. Grillakis, M., Shatah, J. and Strauss, W. (1990) Stability Theory of Solitary Waves in the Presence of Symmetry II. Journal of Functional Analysis, 94, 308-348.
https://doi.org/10.1016/0022-1236(90)90016-E








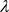 的解
的解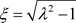 ,下面分析公式(2.20)右边部分,对
关于
展开,并合并 的同阶系数,则
,下面分析公式(2.20)右边部分,对
关于
展开,并合并 的同阶系数,则